Khoảng cách trong không gian - Phương pháp giải nhanh

Trong hình học không gian, khoảng cách là một trong những nội dung quan trọng và thường xuyên xuất hiện nhất trong các kỳ thi tốt nghiệp THPT và đại học. Tuy nhiên, đây cũng là phần kiến thức khiến nhiều học sinh "ám ảnh" vì khó tưởng tượng và dễ nhầm lẫn trong khâu dựng hình. 

Khoảng cách từ một điểm đến một đường thẳng và mặt phẳng 

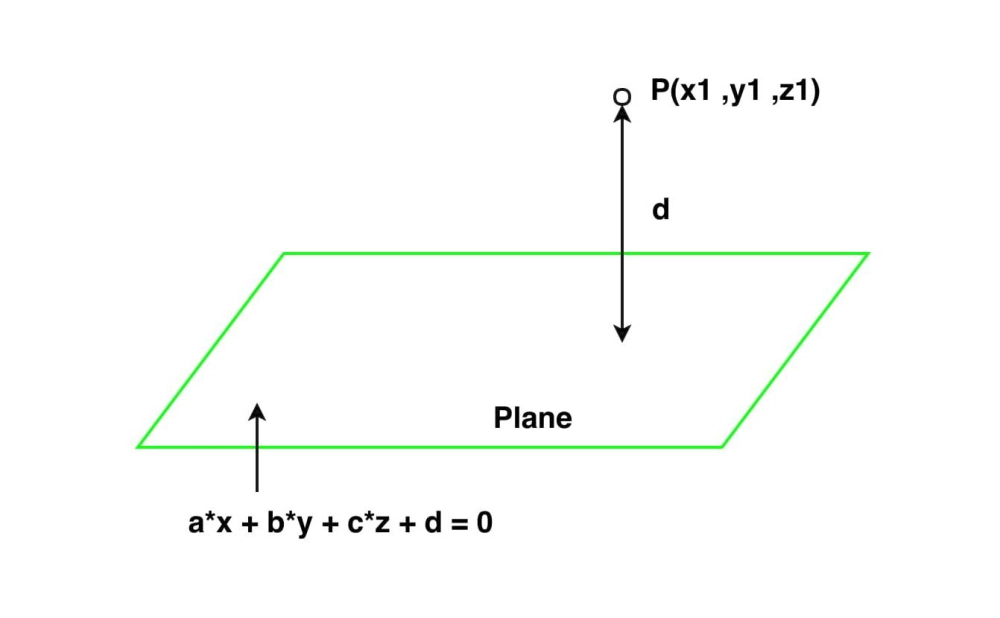
Khoảng cách từ điểm $M$ đến mặt phẳng $(\alpha)$ là độ dài đoạn thẳng $MH$, trong đó $H$ là hình chiếu vuông góc của $M$ lên $(\alpha)$. Ký hiệu là $d(M, (\alpha))$.

Bí quyết xác định hình chiếu $H$

Trong thực tế, để tìm $H$, ta thường đi theo quy trình "2 bước kẻ":

1. Kẻ một mặt phẳng phụ $(\beta)$ đi qua $M$ và vuông góc với $(\alpha)$.
2. Tìm giao tuyến $c = (\alpha) \cap (\beta)$. Khi đó, hình chiếu $H$ chính là hình chiếu của $M$ lên đường thẳng $c$.

Luôn ưu tiên chọn điểm $M$ là chân đường cao của khối chóp (điểm cực tốt) để việc dựng hình trở nên đơn giản nhất. Nếu điểm $M$ không phải chân đường cao, hãy sử dụng kỹ thuật "chuyển khoảng cách" dựa trên định lý Ta-lét.

Khoảng cách giữa đường thẳng và mặt phẳng song song  

Nhiều học sinh lúng túng khi gặp yêu cầu tính khoảng cách giữa hai thực thể lớn. Tuy nhiên, bản chất của chúng đều có thể quy về khoảng cách từ một điểm.

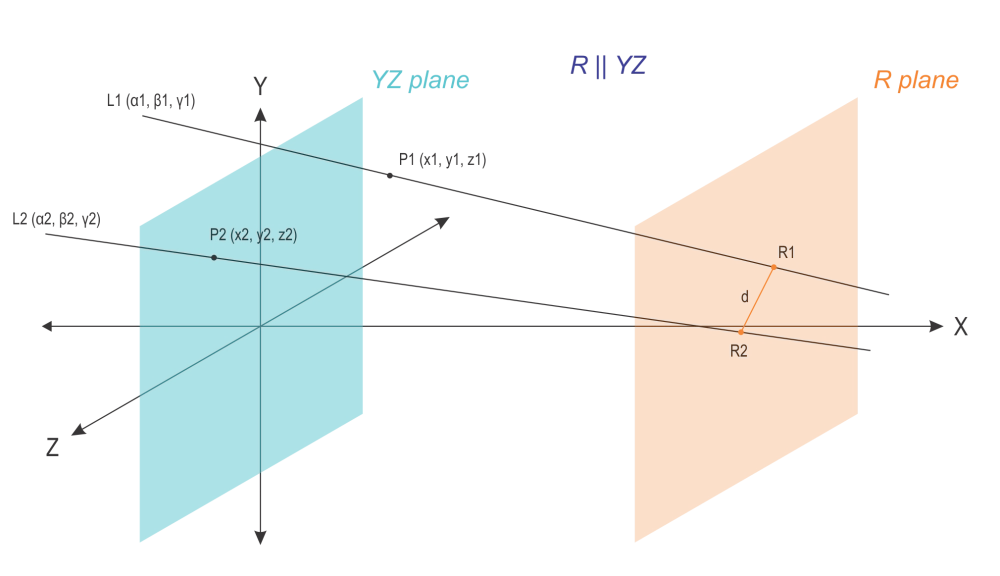
• Đường thẳng $a \parallel (\alpha)$: Khi đó $d(a, (\alpha)) = d(M, (\alpha))$ với $M$ là bất kỳ điểm nào thuộc $a$.
• Hai mặt phẳng $(\alpha) \parallel (\beta)$: Khi đó $d((\alpha), (\beta)) = d(M, (\beta))$ với $M$ là bất kỳ điểm nào thuộc $(\alpha)$.

Lưu ý lỗi sai: Bạn chỉ được phép lấy khoảng cách từ một điểm khi đã chứng minh được tính song song. Nếu hai đối tượng cắt nhau, khoảng cách giữa chúng bằng $0$.

Phương pháp dựng đoạn vuông góc chung và mặt phẳng song song

Đây là dạng toán khó nhất trong hình học không gian thuần túy. Tùy vào đặc điểm của hai đường thẳng $a$ và $b$, ta có hai hướng xử lý:

Cách 1: Dựng đoạn vuông góc chung

Áp dụng khi $a \perp b$. Ta tìm một mặt phẳng $(\alpha)$ chứa $b$ và vuông góc với $a$ tại $I$. Từ $I$ kẻ $IJ \perp b$ tại $J$. Khi đó $IJ$ là đoạn vuông góc chung và $d(a, b) = IJ$.

Cách 2: Sử dụng mặt phẳng song song phụ trợ

Áp dụng khi hai đường thẳng không vuông góc. Ta dựng mặt phẳng $(\alpha)$ chứa $b$ và song song với $a$. Khi đó:

$$d(a, b) = d(a, (\alpha)) = d(M, (\alpha)) \text{ với } M \in a$$

Hệ thống công thức tính khoảng cách trong hệ tọa độ $Oxyz$ 

Đối với các bài thi trắc nghiệm, phương pháp "tọa độ hóa" (gắn hệ trục $Oxyz$) là vũ khí cực mạnh giúp bạn không cần tư duy dựng hình quá nhiều mà vẫn ra đáp án chính xác.

1. Khoảng cách từ điểm $M(x_0; y_0; z_0)$ đến mặt phẳng $(\alpha): Ax + By + Cz + D = 0$:

$$d(M, (\alpha)) = \frac{|Ax_0 + By_0 + Cz_0 + D|}{\sqrt{A^2 + B^2 + C^2}}$$

2. Khoảng cách từ điểm $M$ đến đường thẳng $\Delta$ (đi qua $M_0$, có VTCP $\vec{u}$):

$$d(M, \Delta) = \frac{|[\vec{M_0M}, \vec{u}]|}{|\vec{u}|}$$

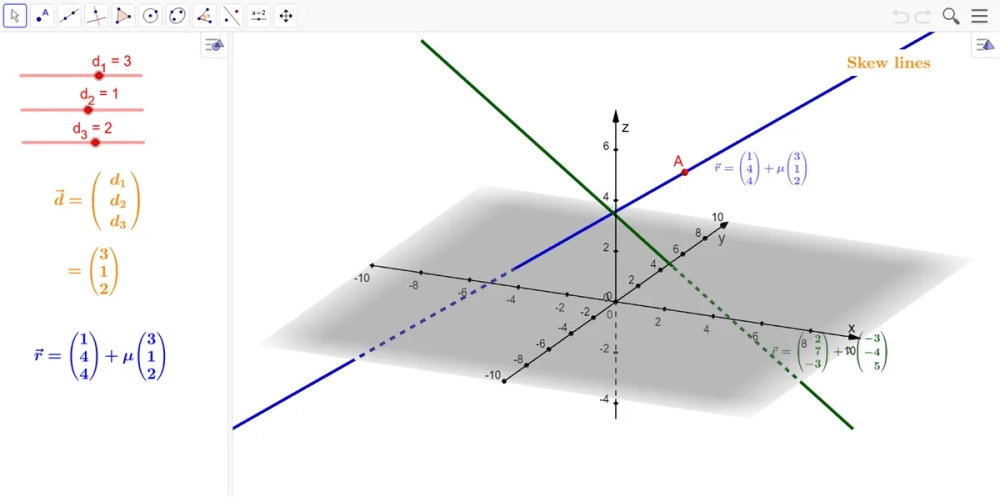
3. Khoảng cách giữa hai đường thẳng chéo nhau $\Delta_1$ và $\Delta_2$:

Sử dụng công thức tích hỗn tạp:

$$d(\Delta_1, \Delta_2) = \frac{|[\vec{u_1}, \vec{u_2}] \cdot \vec{M_1M_2}|}{|[\vec{u_1}, \vec{u_2}]|}$$

Mẹo giải nhanh: Nếu bài toán cho khối đa diện đều hoặc các cạnh vuông góc tại một đỉnh, hãy gắn ngay trục tọa độ $Oxyz$ để biến bài toán hình học thành bài toán đại số, giúp tiết kiệm 50% thời gian làm bài.

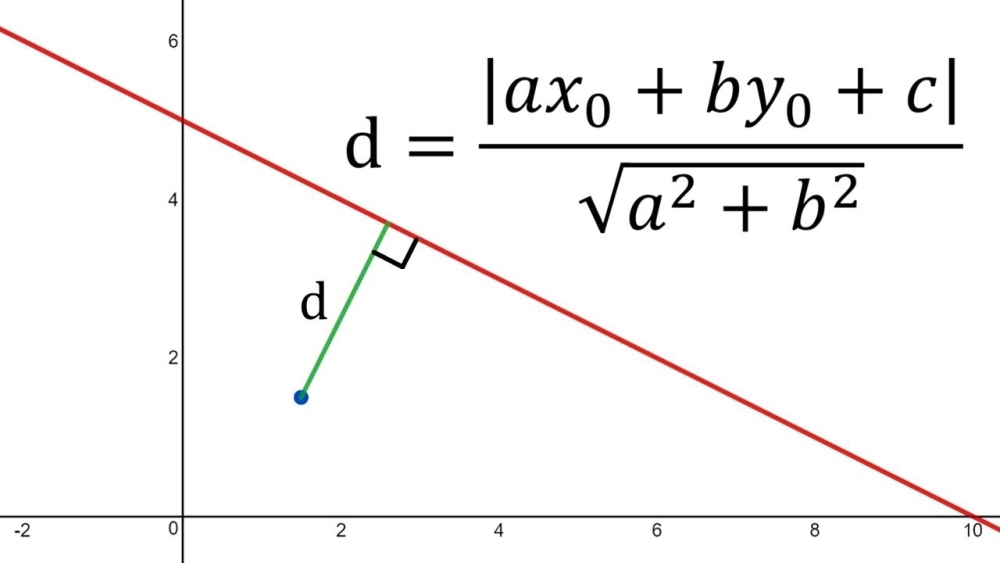
Hy vọng bài viết này đã giúp bạn nắm trọn các phương pháp tính khoảng cách trong không gian. Chìa khóa nằm ở việc: Nếu không gian thuần túy quá khó, hãy dùng Oxyz!

>>> Xem thêm:  

Phương trình đường thẳng trong không gian: Những dạng toán phổ biến

Lý thuyết hệ tọa độ trong không gian: Khái niệm và bài tập cụ thể