Phương trình đường thẳng trong không gian: Những dạng toán phổ biến

Phương trình đường thẳng trong không gian là một trong những chủ đề quan trọng trong chương trình Toán lớp 12. Bài viết này sẽ cung cấp cho bạn hệ thống kiến thức đầy đủ về phương trình đường thẳng trong không gian lớp 12, bao gồm khái niệm, tính chất, phương pháp giải và các dạng bài tập thường gặp.

Phương trình đường thẳng trong không gian là gì?

Phương trình đường thẳng trong không gianlà một biểu thức toán học thể hiện mối liên hệ giữa các tọa độ của các điểm trên đường thẳng đó.

Công thức chung của phương trình đường thẳng trong không gian

Phương trình đường thẳng trong không gian có công thức chung như sau:

\(x = x0 + at\)

\(y = y0 + bt\)

\(z = z0 + ct\)

Trong đó, (x, y, z) là tọa độ của điểm trên đường thẳng, (x0, y0, z0) là tọa độ của một điểm thuộc đường thẳng, và (a, b, c) là vector chỉ phương của đường thẳng.

Để xác định vector chỉ phương của đường thẳng, ta có thể dùng hai điểm thuộc đường thẳng. Khi đó, vector chỉ phương có thể được tính bằng hiệu của tọa độ của hai điểm đó:

[a, b, c] =\([x1 – x0, y1 – y0, z1 – z0]\)

Công thức của phương trình đường thẳng đi qua hai điểm không trùng nhau

Phương trình của đường thẳng đi qua hai điểm A(x₁, y₁) và B(x₂, y₂) không trùng nhau là:

\((y – y₁) / (y₂ – y₁) = (x – x₁) / (x₂ – x₁)\)

Trong công thức này, (x, y) là một điểm bất kỳ trên đường thẳng.

Bước 1: Xác định tọa độ của hai điểm A và B.

Bước 2: Sử dụng công thức trên và thay đổi các giá trị để tính toán phương trình đường thẳng đi qua hai điểm A và B.

Cách viết phương trình đường thẳng song song với một đường thẳng đã biết?

Cách viết phương trình đường thẳng song song với một đường thẳng đã biết là khá đơn giản. Đầu tiên, ta thu được vector chỉ phương của đường thẳng đã biết. Sau đó, ta sử dụng vector chỉ phương này để viết phương trình đường thẳng mới.
Để thu được vector chỉ phương của một đường thẳng, ta có thể lấy hai điểm bất kỳ trên đường thẳng và tính vector chỉ phương giữa hai điểm đó. Sau đó, ta có thể sử dụng vector này để viết phương trình đường thẳng song song mới.
Ví dụ, giả sử chúng ta có đường thẳng đã biết có vector chỉ phương là u = (2, 3). Để viết phương trình đường thẳng song song mới với đường thẳng này, ta sẽ sử dụng vector u để viết phương trình mới.
Phương trình đường thẳng mới có dạng: \((x, y) = (a, b) + t(u)\)
Trong đó, (x, y) là điểm trên đường thẳng mới, (a, b) là một điểm nằm trên đường thẳng cũ, t là một số thực và u là vector chỉ phương của đường thẳng cũ.
Với ví dụ trên, ta có thể lấy một điểm A nằm trên đường thẳng cũ, ví dụ (1, 2), để viết phương trình đường thẳng mới. Phương trình đường thẳng mới sẽ có dạng:
\((x, y) = (1, 2) + t(2, 3)

Phương trình của đường thẳng vuông góc với một đường thẳng đã biết?

Để viết phương trình của một đường thẳng vuông góc với một đường thẳng đã biết, chúng ta cần áp dụng mối quan hệ giữa hai đường thẳng vuông góc.

Bước 1:Xác định hệ số góc của đường thẳng đã biết. Để làm điều này, chúng ta cần xem xét phương trình của đường thẳng đã biết. Ví dụ, nếu phương trình của đường thẳng đã biết là [latex]( y = mx + b )\), với ( m ) là hệ số góc, chúng ta có thể xác định ( m ).

Bước 2:Tính hệ số góc của đường thẳng vuông góc bằng cách lấy nghịch đảo của hệ số góc đã tính ở bước 1. Nghĩa là, hệ số góc của đường thẳng vuông góc là ( -1/m ).

Bước 3:Với hệ số góc đã tính ở bước 2, chúng ta có thể xác định phương trình của đường thẳng vuông góc. Ví dụ, nếu hệ số góc của đường thẳng vuông góc là \( k \), phương trình của đường thẳng vuông góc là \(( y = kx + c )\), với ( c ) là một hằng số tùy ý.

Vậy, để viết phương trình của đường thẳng vuông góc với một đường thẳng đã biết, chúng ta cần xác định hệ số góc của đường thẳng đã biết và tính nghịch đảo của nó, sau đó sử dụng hệ số góc đã tính để xác định phương trình của đường thẳng vuông góc.

Cách viết phương trình đường thẳng đi qua một điểm và song song với một mặt phẳng đã biết

Để viết phương trình của đường thẳng đi qua một điểm và song song với một mặt phẳng đã biết, ta thực hiện các bước sau:

Bước 1: Xác định điểm và mặt phẳng đã biết:

Xác định điểm: Đầu tiên, ta cần biết tọa độ của điểm mà đường thẳng đi qua. Gọi điểm này là Acó tọa độ ( x1,y1,z1)

Xác định mặt phẳng: Sau đó, ta cần biết phương trình mặt phẳng đã biết. Gọi phương trình mặt phẳng này là \(Ax + By + Cz + D= 0\)

Bước 2: Xác định vector chỉ phương của đường thẳng:

Vì đường thẳng cần đi qua điểm Avà song song với mặt phẳng đã biết, nên vector chỉ phương của đường thẳng cần tìm cũng phải song song với vector pháp tuyến của mặt phẳng đã biết.

Vector pháp tuyến của mặt phẳng đã biết có thể xác định bằng các hệ số A, B, C trong phương trình mặt phẳng

Bước 3: Viết phương trình đường thẳng

Với điểm A có tọa độ x1, y1, z1 và vector chỉ phương của đường thẳng, ta có thể viết phương trình đường thẳng như sau:

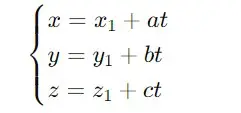
Trong đó (a, b, c) là vector chỉ phương của đường thẳng.

Bước 4:Rút gọn phương trình (nếu cần):

Nếu cần, ta có thể rút gọn phương trình bằng cách chia tỉ lệ cho một số nguyên dương.

Các dạng toán về phương trình đường thẳng trong không gian

Phương trình đường thẳng trong không gian là một chủ đề quan trọng, có nhiều ứng dụng thực tế. Hy vọng qua bài viết này, bạn đã có được những kiến thức nền tảng vững chắc để tiếp tục học tập và nghiên cứu các chủ đề toán học cao hơn.