Giải phương trình bậc 2 - Bí kíp làm chủ công thức Delta

Chào các bạn, trong thế giới đại số, giải phương trình bậc 2 là kỹ năng nền tảng "sống còn" cho bất kỳ ai muốn chinh phục toán học phổ thông. Dưới góc độ giảng viên, tôi nhận thấy nhiều bạn thường máy móc bấm máy tính mà quên mất bản chất logic đằng sau.  

Phương trình bậc 2 là gì? Dạng tổng quát và điều kiện xác định

Phương trình bậc 2 một ẩn là phương trình có dạng tổng quát:

$$ax^2 + bx + c = 0$$

Trong đó:

• $x$ là ẩn số.
• $a, b, c$ là các số thực cho trước (hệ số).
• Điều kiện tiên quyết: $a \neq 0$.

Rất nhiều bạn mất điểm đáng tiếc khi gặp bài toán chứa tham số $m$ (ví dụ: $(m-1)x^2 + 2x + 1 = 0$) mà quên xét trường hợp $a = 0$. Hãy nhớ: Nếu $a = 0$, phương trình sẽ "thoái hóa" thành phương trình bậc nhất, không còn là bậc 2 nữa!

Công thức nghiệm tổng quát và cách tính biệt thức Delta ($\Delta$)

Để giải một phương trình bậc 2 bất kỳ, chúng ta sử dụng biệt thức $\Delta$ (Delta). Đây chính là "linh hồn" quyết định số phận của các nghiệm số.

Công thức tính:

$$\Delta = b^2 - 4ac$$

Dựa vào giá trị của $\Delta$, chúng ta có 3 kịch bản xảy ra:

1. Nếu $\Delta > 0$: Phương trình có 2 nghiệm phân biệt:
   $$x_1 = \frac{-b + \sqrt{\Delta}}{2a}; \quad x_2 = \frac{-b - \sqrt{\Delta}}{2a}$$
2. Nếu $\Delta = 0$: Phương trình có nghiệm kép:
   $$x_1 = x_2 = -\frac{b}{2a}$$
3. Nếu $\Delta < 0$: Phương trình vô nghiệm (trên tập số thực $R$).

Công thức nghiệm thu gọn ($\Delta'$) – Giải pháp tối ưu cho hệ số $b$ chẵn

Một trong những mẹo giúp bạn tính toán nhanh và ít sai sót hơn chính là sử dụng công thức nghiệm thu gọn. Bạn nên dùng cách này khi hệ số $b$ là một số chẵn (tức là $b = 2b'$).

Công thức tính biệt thức thu gọn:

$$\Delta' = (b')^2 - ac$$

Các trường hợp nghiệm tương ứng:

• Nếu $\Delta' > 0$: Có 2 nghiệm phân biệt $x_{1,2} = \frac{-b' \pm \sqrt{\Delta'}}{a}$.
• Nếu $\Delta' = 0$: Có nghiệm kép $x = -\frac{b'}{a}$.
• Nếu $\Delta' < 0$: Phương trình vô nghiệm.

Việc dùng $\Delta'$ giúp các con số nhỏ đi đáng kể, giảm thiểu khả năng tính sai khi không có máy tính bỏ túi.

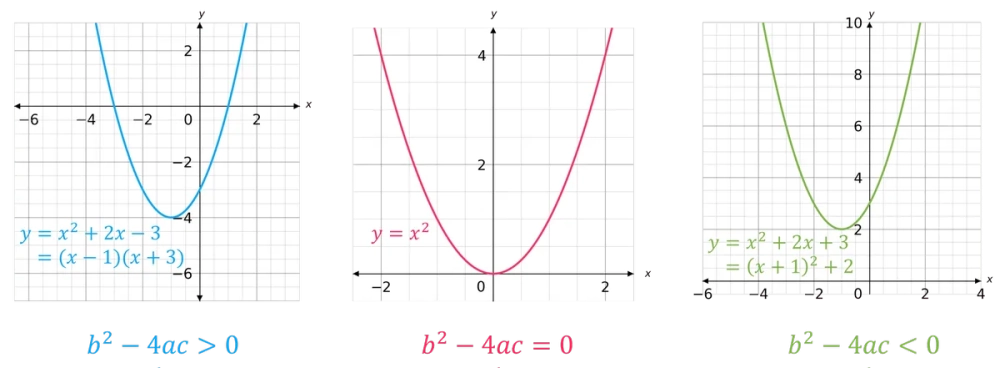
Mối liên hệ giữa đồ thị hàm số bậc 2 và nghiệm của phương trình

Dưới góc nhìn hình học, nghiệm của phương trình $ax^2 + bx + c = 0$ chính là hoành độ giao điểm của đồ thị hàm số bậc 2 (đường Parabol) $y = ax^2 + bx + c$ với trục hoành ($y = 0$).

• Khi $\Delta > 0$: Parabol cắt trục hoành tại 2 điểm riêng biệt.
• Khi $\Delta = 0$: Parabol tiếp xúc với trục hoành tại một điểm (đỉnh của Parabol).
• Khi $\Delta < 0$: Parabol nằm hoàn toàn phía trên hoặc phía dưới trục hoành, không có điểm chung nào.

Việc nắm vững công thức Delta là bước đệm để bạn học tiếp về Định lý Vi-ét và các ứng dụng nâng cao khác. Đừng chỉ học thuộc, hãy thử tự chứng minh công thức này bằng phương pháp tách bình phương một số hạng, bạn sẽ thấy toán học vô cùng thú vị!

>>> Xem ngay bài viết: 

• Tổng hợp công thức nghiệm của phương trình bậc hai
• Cách xây dựng phương trình hồi quy tuyến tính