Bất đẳng thức Cauchy - Kỹ thuật chọn điểm rơi và mẹo tìm Min/Max đỉnh cao
Khám phá kỹ thuật "chọn điểm rơi", mẹo tìm Min/Max và cách ghép cặp nghịch đảo trong bất đẳng thức Cauchy giúp học sinh chinh phục mọi bài toán cực trị.
Chào các bạn, trong thế giới của những con số và đại lượng, bất đẳng thức Cauchy (hay còn gọi là bất đẳng thức AM-GM) được ví như "vương trượng" giúp ta giải quyết các bài toán cực trị một cách thanh thoát. Tuy nhiên, không ít bạn học sinh cảm thấy bế tắc khi áp dụng máy móc mà không hiểu bản chất của "sự cân bằng".
Kỹ thuật "chọn điểm rơi" trong bất đẳng thức Cauchy
Sai lầm lớn nhất khi học bất đẳng thức là chỉ thuộc lòng công thức mà quên mất điều kiện xảy ra dấu đẳng thức. Kỹ thuật "chọn điểm rơi" chính là việc dự đoán giá trị của các biến số khi biểu thức đạt cực trị.
Dấu đẳng thức trong Cauchy cho $n$ số không âm $a_1, a_2, ..., a_n$ xảy ra khi và chỉ khi:
$$a_1 = a_2 = ... = a_n$$
Tại sao phải chọn điểm rơi?
Nếu bạn áp dụng Cauchy không đúng lúc, dấu đẳng thức sẽ không xảy ra, dẫn đến kết quả đánh giá bị sai hoàn toàn.
- Ví dụ: Cho $a \ge 2$, tìm giá trị nhỏ nhất của $A = a + \frac{1}{a}$.
Nếu bạn dùng Cauchy ngay: $a + \frac{1}{a} \ge 2\sqrt{a \cdot \frac{1}{a}} = 2$. Tuy nhiên, dấu "=" xảy ra khi $a = \frac{1}{a} \Rightarrow a = 1$ (vô lý vì $a \ge 2$). - Giải pháp: Ta dự đoán điểm rơi tại $a = 2$. Từ đó, ta tách $A$ thành các phần sao cho dấu "=" thỏa mãn tại $a = 2$.

Ứng dụng Cauchy để tìm giá trị nhỏ nhất (Min) của biểu thức
Để tìm giá trị nhỏ nhất (Min), chúng ta thường thực hiện đánh giá từ trung bình cộng sang trung bình nhân. Mục tiêu tối thượng là "triệt tiêu" được biến số để đưa về một hằng số.
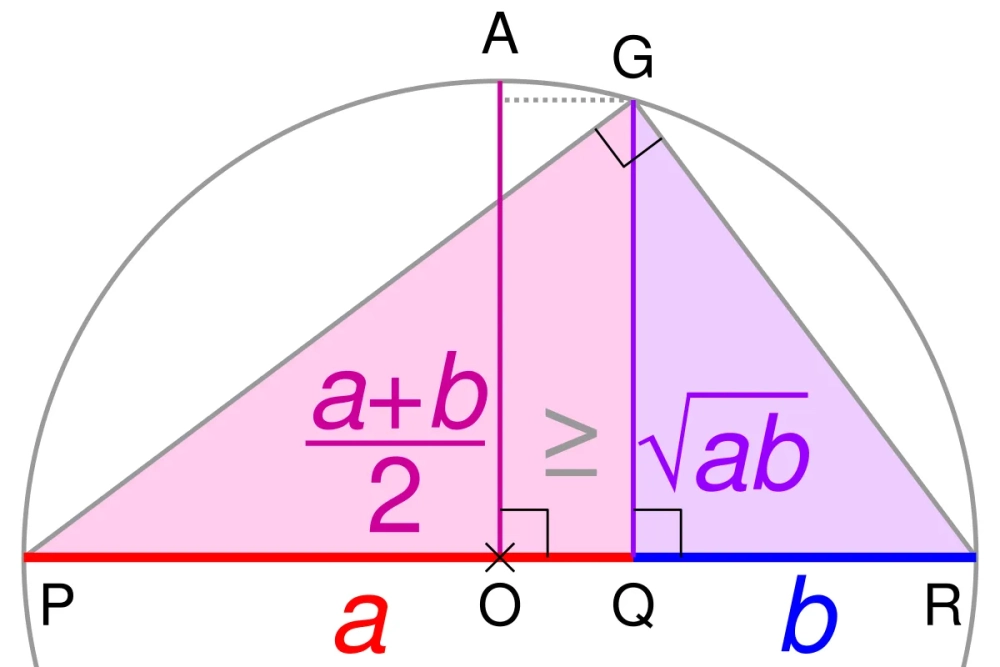
Công thức cơ bản cho hai số không âm $a, b$:
$$\frac{a + b}{2} \ge \sqrt{ab} \Rightarrow a + b \ge 2\sqrt{ab}$$
Khi muốn tìm Min của biểu thức dạng $f(x) + g(x)$, ta cần cấu trúc sao cho tích $f(x) \cdot g(x)$ là một hằng số.
Mẹo giải nhanh: Nếu biểu thức có chứa biến ở cả tử và mẫu, hãy quan sát xem có thể nhân thêm hằng số hoặc thêm bớt để khi nhân lại, các biến số bị "tự sát" (triệt tiêu lẫn nhau) hay không.
Cách tìm giá trị lớn nhất (Max) bằng phương pháp đánh giá ngược
Trái ngược với việc tìm Min, khi tìm giá trị lớn nhất (Max), ta cần chặn trên biểu thức. Chúng ta sẽ đánh giá từ trung bình nhân sang trung bình cộng.
$$\sqrt{ab} \le \frac{a + b}{2} \Rightarrow ab \le \left(\frac{a + b}{2}\right)^2$$
Kỹ thuật này cực kỳ hiệu quả đối với các bài toán có dạng tích của các biến mà tổng của chúng là một hằng số.
- Ví dụ: Cho $x + y = 10$, tìm Max của $P = x \cdot y$.
Áp dụng Cauchy: $xy \le \left(\frac{x+y}{2}\right)^2 = \left(\frac{10}{2}\right)^2 = 25$.
Phương pháp thêm bớt, ghép cặp nghịch đảo để áp dụng Cauchy hiệu quả
Đây là kỹ thuật "ảo thuật" nhất trong bất đẳng thức. Đôi khi, các biến số không nằm ở vị trí thuận lợi để triệt tiêu. Khi đó, ta cần thêm bớt hoặc ghép cặp.
- Ghép cặp nghịch đảo: Nếu có $x$, hãy tìm cách tạo ra $\frac{k}{x}$ để khi nhân chúng lại ta có một hằng số.
- Kỹ thuật tách hạng tử: Đối với các bài toán có điều kiện ràng buộc (như $a+b+c=k$), ta thường tách các số hạng để tận dụng giả thiết.
- Ví dụ điển hình: Cho $x > 1$, tìm Min của $P = x + \frac{4}{x-1}$.
- Ta thấy mẫu số là $x-1$, nhưng tử số chỉ là $x$.
- Thêm bớt: $P = (x-1) + \frac{4}{x-1} + 1$.
- Áp dụng Cauchy cho hai số đầu: $(x-1) + \frac{4}{x-1} \ge 2\sqrt{(x-1) \cdot \frac{4}{x-1}} = 4$.
- Vậy $P_{min} = 4 + 1 = 5$.

Bất đẳng thức Cauchy không chỉ là một công thức, nó là nghệ thuật của sự cân bằng. Chỉ khi bạn xác định đúng "điểm rơi", các đánh giá của bạn mới thực sự có giá trị và đưa đến đáp số đúng. Hãy luôn kiểm tra dấu đẳng thức ngay sau khi đặt bút viết dấu $\ge$.
>>> Đọc thêm:
Bài Viết Liên Quan
Tác giả Phương Mai – Người truyền lửa tại toanhoc.edu.vn. Với chuyên môn Toán học chuyên sâu, cô chia sẻ kiến thức tư duy logic và phương pháp giải toán sáng tạo giúp học sinh làm chủ mọi con số.







