Ma trận và Định thức - Toàn tập kiến thức từ cơ bản đến chuyên sâu

Chào các bạn, trong toán học hiện đại và đặc biệt là trong lĩnh vực trí tuệ nhân tạo hay xác suất thống kê, Ma trận và Định thức đóng vai trò như những "viên gạch" nền tảng. Dưới góc độ giảng viên, tôi thấy nhiều sinh viên thường bị choáng ngợp bởi những con số xếp hàng dài dằng dặc, nhưng thực tế, ma trận chỉ là một cách sắp xếp dữ liệu cực kỳ logic.  

Ma trận là gì? Các loại ma trận đặc biệt trong toán học

Về bản chất, một ma trận cấp $m \times n$ là một bảng chữ nhật gồm $m$ dòng và $n$ cột, chứa các số thực hoặc số phức. Chúng ta thường ký hiệu ma trận bằng các chữ cái in hoa như $A, B, C$.

Để việc tính toán trở nên đơn giản, bạn cần làm quen với các "nhân vật" đặc biệt sau:

• Ma trận vuông: Có số dòng bằng số cột ($m = n$). Đây là loại ma trận duy nhất có định thức.
• Ma trận đơn vị ($I$): Là ma trận vuông có các phần tử trên đường chéo chính bằng $1$, còn lại bằng $0$. Nó đóng vai trò như số $1$ trong phép nhân số thực.
• Ma trận không ($O$): Tất cả các phần tử đều bằng $0$.
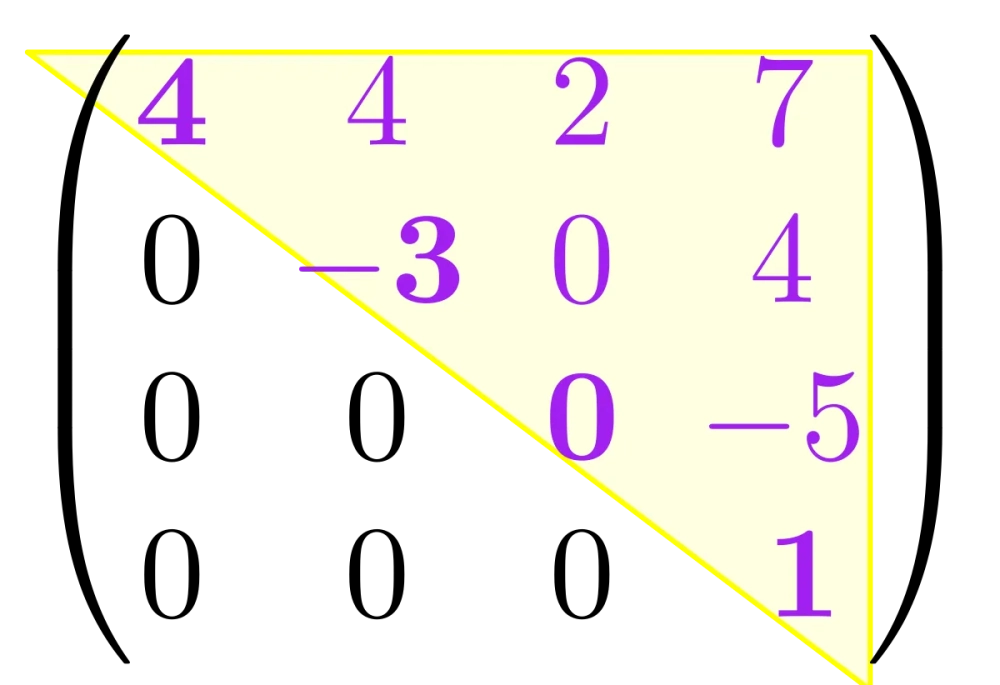
• Ma trận tam giác: Các phần tử nằm trên hoặc dưới đường chéo chính đều bằng $0$. Loại ma trận này cực kỳ "dễ tính" khi cần tìm định thức.

Các phép toán cơ bản trên ma trận 

Đây là phần dễ gây nhầm lẫn nhất nếu bạn không nắm vững điều kiện tiên quyết của mỗi phép toán.

• Phép cộng và trừ: Chỉ thực hiện được khi hai ma trận có cùng cấp. Bạn chỉ cần cộng/trừ các phần tử ở vị trí tương ứng.
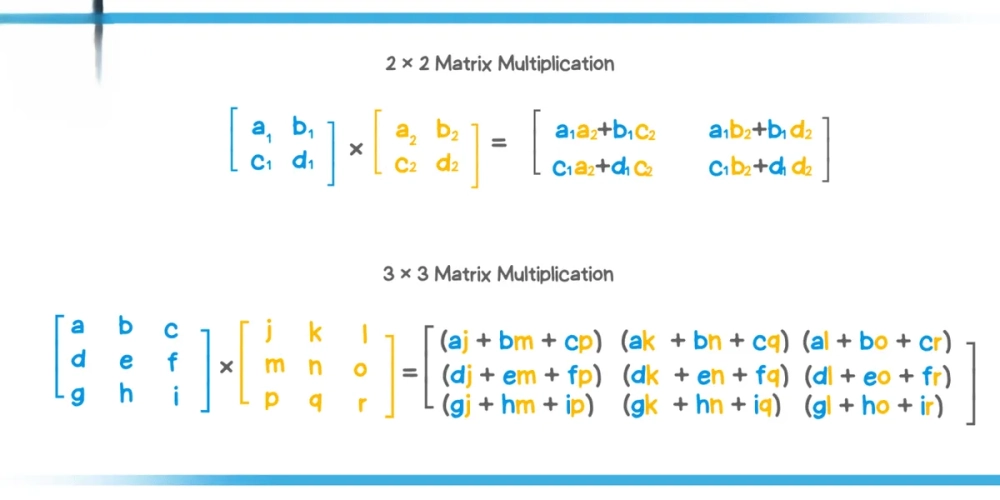
• Phép nhân (Ma trận với Ma trận): Đây là "bẫy" kinh điển. Để tính được $A \cdot B$, thì số cột của $A$ phải bằng số dòng của $B$.
• Công thức: $c_{ij} = \sum_{k=1}^{n} a_{ik} b_{kj}$ (Dòng nhân Cột).
• Lưu ý: Phép nhân ma trận không có tính chất giao hoán ($A \cdot B \neq B \cdot A$).
• Phép chuyển vị ($A^T$): Đơn giản là biến dòng thành cột và biến cột thành dòng.

Khi nhân hai ma trận, hãy dùng ngón tay trái rà theo dòng của ma trận $A$ và ngón tay phải rà theo cột của ma trận $B$. Điều này giúp bạn không bao giờ bị lệch vị trí các phần tử.

Định thức và các tính chất cốt lõi cần nhớ

Định thức, ký hiệu là $\det(A)$ hoặc $|A|$, là một giá trị số đặc trưng cho một ma trận vuông. Nó cho biết nhiều thông tin về "sức khỏe" của ma trận đó, chẳng hạn như ma trận có bị biến dạng hay không khi thực hiện các phép biến đổi không gian.

Các tính chất giúp bạn giải toán trắc nghiệm "thần tốc":

1. Nếu ma trận có một dòng (hoặc cột) toàn số $0$, thì $\det(A) = 0$.
2. Nếu hai dòng (hoặc cột) của ma trận tỉ lệ với nhau hoặc giống hệt nhau, thì $\det(A) = 0$.
3. $\det(A \cdot B) = \det(A) \cdot \det(B)$.
4. Khi đổi chỗ hai dòng cho nhau, định thức sẽ đổi dấu.

Mối liên hệ giữa định thức và sự tồn tại của ma trận nghịch đảo

Ma trận nghịch đảo, ký hiệu là $A^{-1}$, là ma trận sao cho $A \cdot A^{-1} = A^{-1} \cdot A = I$. Tuy nhiên, không phải ma trận vuông nào cũng có "người đồng hành" này.

Điều kiện cần và đủ: Ma trận vuông $A$ có nghịch đảo khi và chỉ khi nó là ma trận không suy biến, tức là:

$$\det(A) \neq 0$$

Nếu $\det(A) = 0$, ma trận đó được gọi là ma trận suy biến (singular matrix) và chúng ta không thể tìm được ma trận nghịch đảo của nó. Trong thực tế, việc tính $\det(A)$ là bước đầu tiên và quan trọng nhất trước khi bạn bắt tay vào tìm $A^{-1}$ bằng phương pháp ma trận phụ hợp hay biến đổi dòng sơ cấp Gauss-Jordan.

Ma trận và định thức không hề đáng sợ nếu bạn nắm chắc các quy tắc về "dòng" và "cột". Hãy luôn kiểm tra điều kiện cấp của ma trận trước khi thực hiện bất kỳ phép toán nào để tránh những sai sót đáng tiếc.