Mặt cầu ngoại tiếp - Cách xác định tâm và công thức giải nhanh
Hướng dẫn toàn tập về mặt cầu ngoại tiếp: điều kiện tồn tại, cách xác định tâm và công thức tính nhanh bán kính, diện tích, thể tích dành cho học sinh THPT.
Trong hình học không gian lớp 12, mặt cầu ngoại tiếp là một trong những chủ đề quan trọng nhất, xuất hiện dày đặc trong các đề thi tốt nghiệp THPT và đánh giá năng lực. Việc hiểu rõ bản chất "đồng cách" và nắm vững công thức tính nhanh bán kính sẽ giúp bạn giải quyết các câu hỏi trắc nghiệm chỉ trong vài giây.
Mặt cầu ngoại tiếp là gì? Định nghĩa và điều kiện tồn tại
Một mặt cầu được gọi là ngoại tiếp một khối đa diện nếu tất cả các đỉnh của đa diện đó đều nằm trên mặt cầu. Khi đó, khối đa diện được gọi là nội tiếp mặt cầu.
Không phải khối đa diện nào cũng có mặt cầu ngoại tiếp. Bạn cần ghi nhớ điều kiện tiên quyết này để tránh làm bài vô nghĩa:
- Đối với hình chóp: Một hình chóp có mặt cầu ngoại tiếp khi và chỉ khi đáy của nó là một đa giác nội tiếp đường tròn (ví dụ: đáy là tam giác, hình vuông, hình chữ nhật, hình thang cân).
- Đối với hình lăng trụ: Một hình lăng trụ có mặt cầu ngoại tiếp khi và chỉ khi nó là lăng trụ đứng và có đáy là đa giác nội tiếp đường tròn.
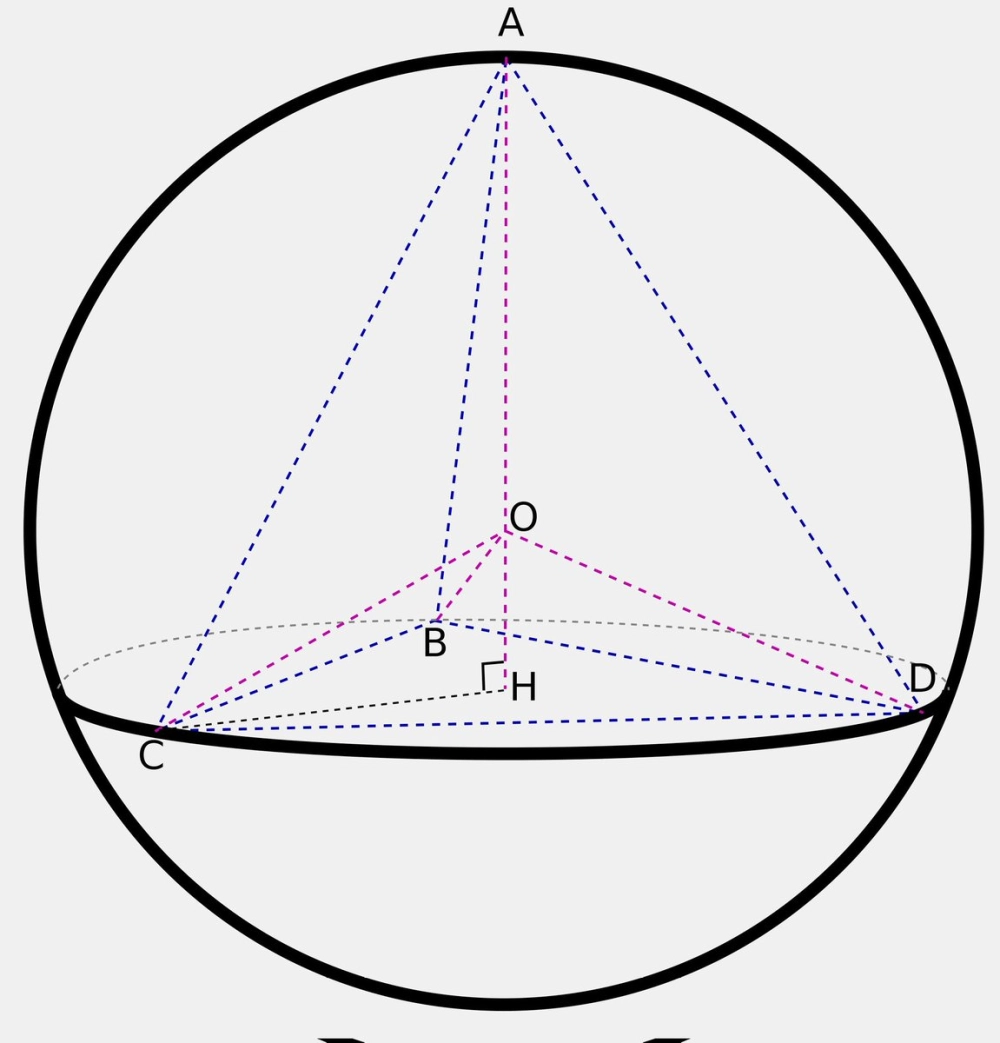
Cách xác định tâm mặt cầu ngoại tiếp khối đa diện
Tâm mặt cầu ngoại tiếp $I$ là điểm cách đều tất cả các đỉnh của khối đa diện. Để tìm $I$, chúng ta thường thực hiện theo quy trình "trục và mặt phẳng trung trực" như sau:
- Bước 1: Tìm trục của đáy ($\Delta$): Xác định tâm $O$ của đường tròn ngoại tiếp đa giác đáy. Đường thẳng $\Delta$ đi qua $O$ và vuông góc với mặt phẳng đáy được gọi là trục đường tròn đáy. Mọi điểm trên $\Delta$ đều cách đều các đỉnh của đáy.
- Bước 2: Tìm mặt phẳng trung trực (hoặc đường trung trực): Xét một cạnh bên (ví dụ $SA$). Dựng mặt phẳng trung trực $(P)$ của đoạn $SA$.
- Bước 3: Xác định tâm: Giao điểm $I = \Delta \cap (P)$ chính là tâm mặt cầu ngoại tiếp cần tìm.
Tổng hợp công thức tính bán kính ($R$) mặt cầu ngoại tiếp thường gặp
Để tối ưu thời gian làm bài trắc nghiệm, bạn nên thuộc lòng các công thức "vạn năng" cho các khối hình đặc biệt sau:
- Hình hộp chữ nhật (cạnh $a, b, c$):
$$R = \frac{\sqrt{a^2 + b^2 + c^2}}{2}$$ - Hình lập phương (cạnh $a$):
$$R = \frac{a\sqrt{3}}{2}$$ - Hình chóp có cạnh bên vuông góc với đáy (chiều cao $h$, bán kính đáy $R_d$):
$$R = \sqrt{R_d^2 + \left(\frac{h}{2}\right)^2}$$ - Tứ diện đều (cạnh $a$):
$$R = \frac{a\sqrt{6}}{4}$$
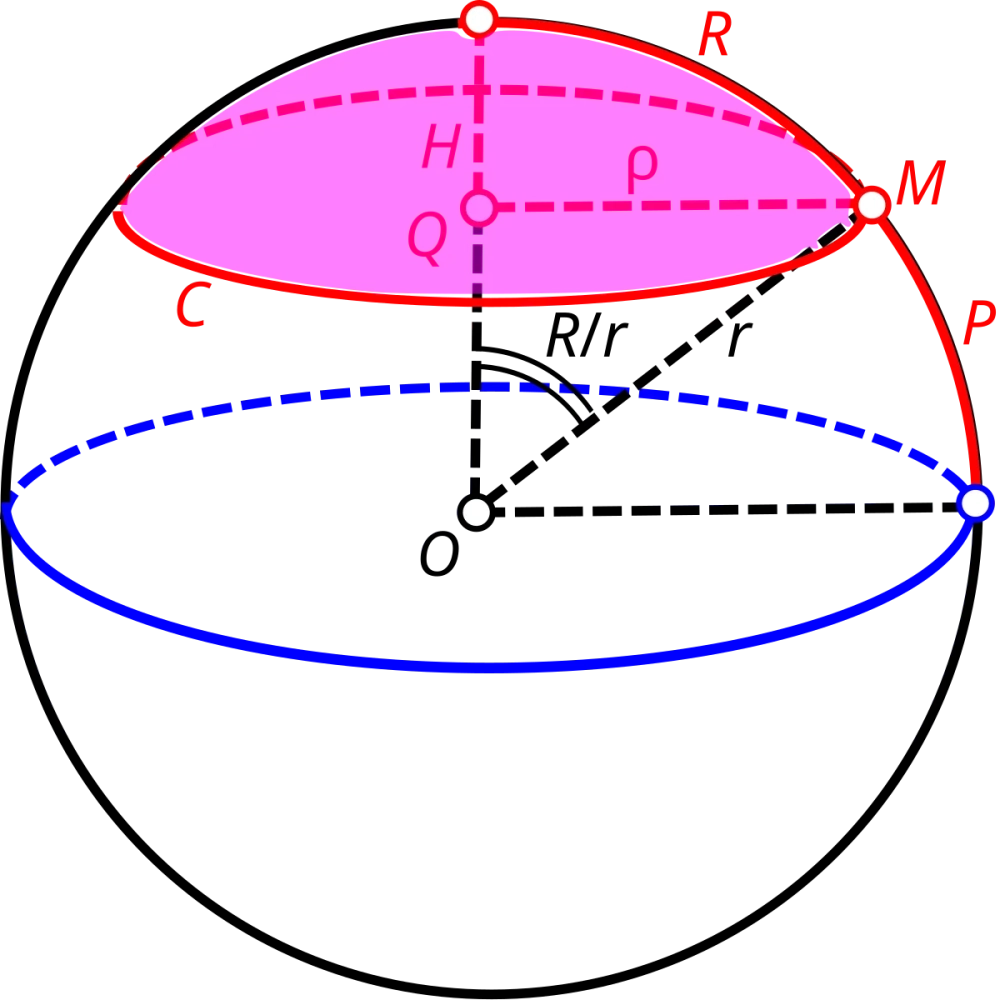
Công thức tính diện tích và thể tích mặt cầu ngoại tiếp
Sau khi đã xác định được bán kính $R$, việc tính toán các thông số còn lại trở nên cực kỳ đơn giản. Hãy đảm bảo bạn không nhầm lẫn giữa công thức diện tích ($R^2$) và thể tích ($R^3$):
- Diện tích mặt cầu ($S$):
$$S = 4\pi R^2$$ - Thể tích khối cầu ($V$):
$$V = \frac{4}{3}\pi R^3$$
Lưu ý lỗi sai: Học sinh thường quên số $4$ trong công thức diện tích hoặc quên lũy thừa $3$ trong công thức thể tích. Hãy nhớ rằng diện tích là đơn vị vuông ($^2$), còn thể tích là đơn vị khối ($^3$).
Khi gặp bài toán mặt cầu ngoại tiếp, hãy luôn đặt câu hỏi "Chân đường cao rơi vào đâu?". Nếu chân đường cao trùng với tâm đường tròn ngoại tiếp đáy (hình chóp đều), tâm mặt cầu chắc chắn nằm trên đường cao đó.
Làm chủ kiến thức về mặt cầu ngoại tiếp đòi hỏi bạn phải kết hợp nhuần nhuyễn giữa khả năng tưởng tượng hình học và kỹ năng tính toán đại số. Hãy bắt đầu bằng việc xác định loại hình chóp, sau đó áp dụng công thức tính $R$ tương ứng để đạt kết quả nhanh nhất. Đừng quên vẽ hình phác thảo trục đường tròn đáy để tránh nhầm lẫn vị trí tâm.
>>> Đọc nhiều hơn:
- Phương trình mặt cầu: Định nghĩa, công thức và ví dụ chi tiết
- Công thức tính diện tích mặt cầu và giải bài tập
Bài Viết Liên Quan
Tác giả Phương Mai – Người truyền lửa tại toanhoc.edu.vn. Với chuyên môn Toán học chuyên sâu, cô chia sẻ kiến thức tư duy logic và phương pháp giải toán sáng tạo giúp học sinh làm chủ mọi con số.







