Xác suất cổ điển - Quy trình giải nhanh và mẹo tránh bẫy

Chào các bạn, trong thế giới toán học, xác suất cổ điển là một trong những phần kiến thức "dễ ăn điểm" nhất nếu bạn nắm vững quy trình logic. Tuy nhiên, đây cũng là nơi "hố đen" của những sai sót trong khâu đếm không gian mẫu. 

Quy trình 3 bước giải bài toán xác suất cổ điển nhanh gọn

Để giải quyết một bài toán xác suất mà không bị rối, bạn cần tuân thủ nghiêm ngặt quy trình "Phễu ngược" sau đây:

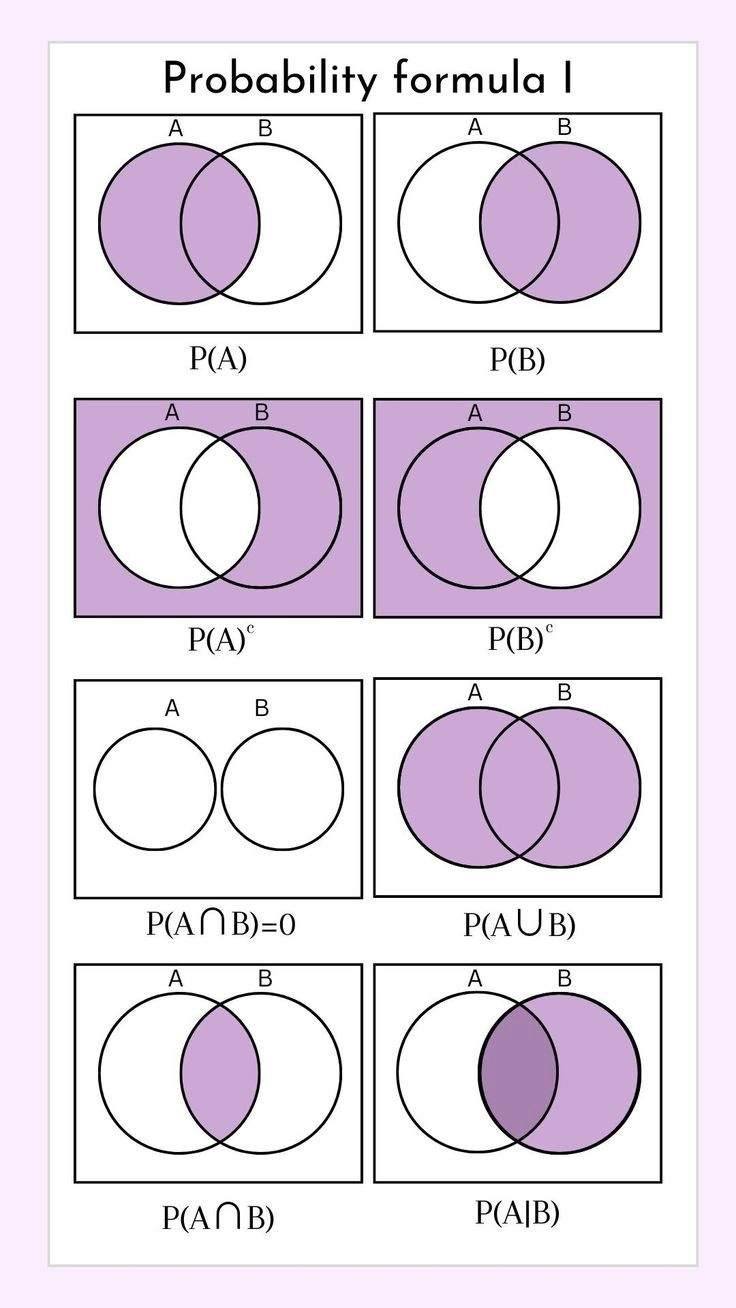
• Bước 1: Xác định không gian mẫu ($\Omega$): Đây là tập hợp tất cả các kết quả có thể xảy ra của phép thử. Hãy tính số phần tử của không gian mẫu $n(\Omega)$. Lưu ý: Đọc kỹ đề để xem có sự phân biệt thứ tự hay không.
• Bước 2: Xác định biến cố thuận lợi ($A$): Đếm số kết quả xảy ra thỏa mãn yêu cầu bài toán $n(A)$. Đây thường là bước khó nhất, đòi hỏi kỹ năng phân tích trường hợp.
• Bước 3: Lập tỉ số: Áp dụng định nghĩa xác suất cổ điển để đưa ra đáp án cuối cùng:
  $$P(A) = \frac{n(A)}{n(\Omega)}$$
  (Điều kiện: $0 \leq P(A) \leq 1$)

Ứng dụng tổ hợp và chỉnh hợp trong tính xác suất cổ điển

Khi các tập hợp trở nên quá lớn, việc liệt kê thủ công là không thể. Đây là lúc chúng ta cần đến sức mạnh của Đại số tổ hợp.

• Sử dụng Tổ hợp ($C_n^k$): Dùng khi bạn chọn một nhóm phần tử mà không quan tâm đến thứ tự. Ví dụ: Chọn 3 viên bi từ hộp 10 viên, chọn 2 học sinh đi trực nhật.
  $$C_n^k = \frac{n!}{k!(n-k)!}$$
• Sử dụng Chỉnh hợp ($A_n^k$): Dùng khi việc chọn có kèm theo việc sắp xếp thứ tự hoặc phân công chức vụ. Ví dụ: Chọn 3 bạn làm Lớp trưởng, Lớp phó, Bí thư; lấy lần lượt từng viên bi từ hộp.
  $$A_n^k = \frac{n!}{(n-k)!}$$

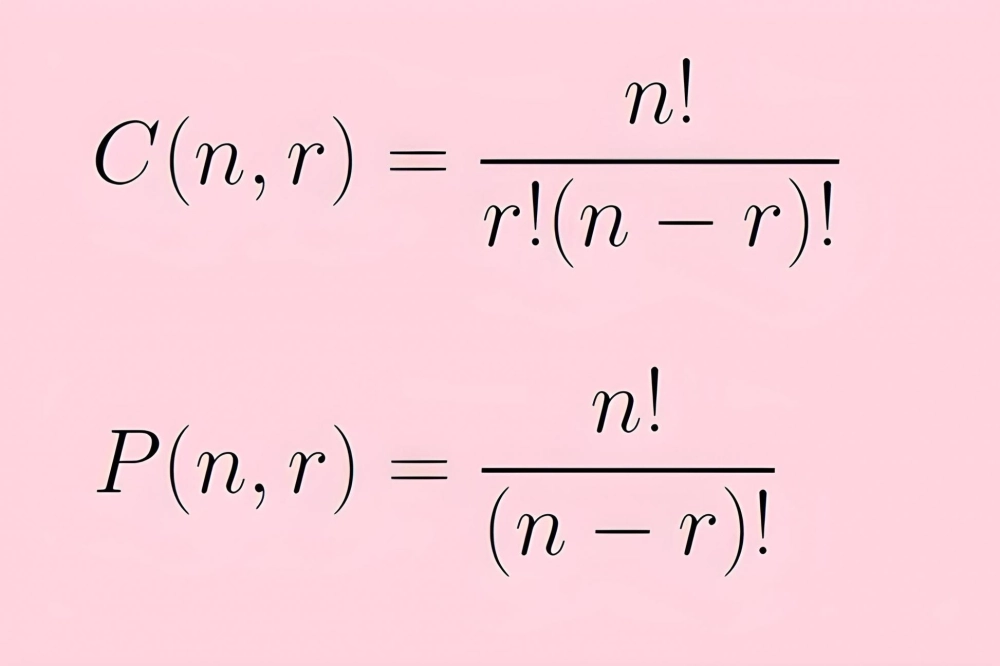
Tổng hợp các dạng bài tập xác suất cổ điển thường gặp trong đề thi

Dưới đây là các "đặc sản" luôn xuất hiện trong các đề thi THPT Quốc gia và đề thi đại học:

• Dạng con súc sắc: Thường là tung 2 con súc sắc đồng chất. Không gian mẫu là $6 \times 6 = 36$. Các bài toán thường hỏi về tổng số chấm, tích số chấm hoặc số chấm xuất hiện giống nhau.
• Dạng đồng xu: Tung $n$ lần đồng xu. Không gian mẫu là $2^n$. Bài toán thường yêu cầu tính xác suất xuất hiện $k$ mặt ngửa.
• Dạng bộ bài tú lơ khơ (52 lá): Yêu cầu tính xác suất rút được các lá bài cùng chất, cùng số hoặc các lá bài đặc biệt như Át (Ace), J, Q, K.
• Dạng hộp bi (Hộp kín): Bốc ngẫu nhiên các viên bi khác màu. Đây là dạng toán kiểm tra kỹ năng dùng quy tắc cộng và quy tắc nhân tốt nhất.

Những sai lầm kinh điển khiến bạn mất điểm khi tính xác suất

Ngay cả những học sinh giỏi cũng thường xuyên rơi vào "bẫy" cảm giác. Hãy lưu ý các điểm sau để không mất điểm đáng tiếc:

1. Nhầm lẫn giữa Tổ hợp và Chỉnh hợp: Đây là lỗi phổ biến nhất. Như đã nói ở trên, hãy luôn kiểm tra yếu tố "thứ tự".
2. Đếm trùng hoặc liệt kê thiếu: Đặc biệt là trong các bài toán chia trường hợp. Để khắc phục, hãy sử dụng sơ đồ cây hoặc bảng hệ thống.
3. Không xác định đúng phép thử: Nhiều bạn bắt tay vào đếm biến cố $A$ khi chưa định hình rõ không gian mẫu $\Omega$ là gì, dẫn đến việc mẫu số và tử số không tương thích về logic (ví dụ tử số có thứ tự nhưng mẫu số thì không).
4. Lỗi "ít nhất": Với các bài toán có từ "ít nhất một", hãy ưu tiên sử dụng biến cố đối ($\bar{A}$) để tính toán nhanh hơn: $P(A) = 1 - P(\bar{A})$.

Xác suất cổ điển không khó, cái khó là sự tỉ mỉ trong khâu đếm. Hãy luyện tập với quy trình 3 bước để tạo thành phản xạ tự nhiên.

>>> Có thể bạn quan tâm: 

• Phân tích phương sai trong thống kê

• Định nghĩa và tính chất của phân phối chuẩn