Lý thuyết và công thức tính chu vi hình thang
Chu vi hình thang là một khái niệm toán học quan trọng, được sử dụng để tính toán tổng độ dài của tất cả các cạnh của hình thang. Hiểu biết về chu vi hình thang đóng vai trò thiết
Chu vi hình thang là một khái niệm toán học quan trọng, được sử dụng để tính toán tổng độ dài của tất cả các cạnh của hình thang. Hiểu biết về chu vi hình thang đóng vai trò thiết yếu trong việc giải các bài toán liên quan đến hình thang, cũng như ứng dụng trong thực tế.
Khái niệm hình thang
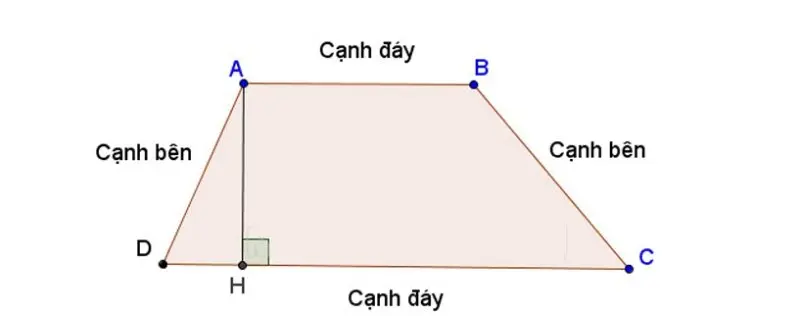
Hình thang là tứ giác lồi có hai cạnh đối diện song song.
Chu vi hình thang là tổng độ dài của bốn cạnh của hình thang.
Công thức tính chu vi hình thang
P = a + b + c + d
trong đó:
- P là chu vi hình thang
- a và b là độ dài hai đáy của hình thang
- c và d là độ dài hai cạnh bên của hình thang
Công thức tính chu vi hình thang cân
P = 2(a + b)
trong đó:
- P là chu vi hình thang cân
- a và b là độ dài hai đáy của hình thang cân
Lưu ý:
- Công thức trên áp dụng cho tất cả các loại hình thang (hình thang cân, hình thang vuông,…)
- Nếu hai cạnh bên của hình thang bằng nhau thì ta có thể sử dụng công thức sau để tính chu vi:
P = a + b + 2c
trong đó: c là độ dài cạnh bên
Các dạng bài tập và phương pháp giải về chu vi hình thang
Dạng 1: Cho độ dài các cạnh của hình thang, tính chu vi hình thang.
Phương pháp giải:
Áp dụng công thức tính chu vi hình thang:
P = a + b + c + d
trong đó:
- P là chu vi hình thang
- a và b là độ dài hai cạnh đáy
- c và d là độ dài hai cạnh bên
Ví dụ:
Cho hình thang ABCD có AB = 5cm, CD = 7cm, AD = 4cm và BC = 6cm. Chu vi hình thang ABCD là:
P = AB + BC + CD + DA = 5 + 6 + 7 + 4 = 22cm
Dạng 2: Cho chu vi hình thang và một số dữ kiện khác (độ dài một cạnh, hai cạnh,…) để tính độ dài các cạnh còn lại của hình thang.
Phương pháp giải:
Lập phương trình dựa vào công thức tính chu vi hình thang và các dữ kiện đề bài cho.
Giải phương trình để tìm độ dài các cạnh còn lại của hình thang.
Ví dụ:
Cho hình thang ABCD có chu vi là 34cm và AB = 8cm. Tính độ dài cạnh CD.
Giải:
Gọi độ dài cạnh CD là x.
Theo công thức tính chu vi hình thang, ta có:
P = AB + BC + CD + DA = 8 + x + x + 8 = 34
Suy ra: 2x = 18
Vậy: x = 9
Độ dài cạnh CD là 9cm.
Dạng 3: Vận dụng tính chất của hình thang (hình thang cân, hình thang vuông,…) để giải bài tập.
Phương pháp giải:
- Sử dụng các tính chất của hình thang (hình thang cân, hình thang vuông,…) để biến đổi bài toán về dạng đơn giản hơn.
- Áp dụng công thức tính chu vi hình thang để giải bài toán.
Ví dụ:
Cho hình thang cân ABCD có AB = 8cm, BC = 6cm và AD = 5cm. Tính chu vi hình thang ABCD.
Giải:
Vì hình thang ABCD là hình thang cân nên AB = CD = 8cm.
Chu vi hình thang ABCD là:
P = AB + BC + CD + DA = 8 + 6 + 8 + 5 = 27cm
Bài tập về chu vi hình thang có lời giải
Bài 1: Cho hình thang ABCD có AB = 5cm, CD = 7cm, AD = 4cm và BC = 6cm. Tính chu vi hình thang ABCD.
Giải:
Chu vi hình thang ABCD là:
P = AB + BC + CD + DA = 5 + 6 + 7 + 4 = 22cm
Bài 2: Cho hình thang ABCD có chu vi là 34cm và AB = 8cm. Tính độ dài cạnh CD.
Giải:
Gọi độ dài cạnh CD là x.
Theo công thức tính chu vi hình thang, ta có:
P = AB + BC + CD + DA = 8 + x + x + 8 = 34
Suy ra: 2x = 18
Vậy: x = 9
Độ dài cạnh CD là 9cm.
Bài 3: Cho hình thang cân ABCD có AB = 8cm, BC = 6cm và AD = 5cm. Tính chu vi hình thang ABCD.
Giải:
Vì hình thang ABCD là hình thang cân nên AB = CD = 8cm.
Chu vi hình thang ABCD là:
P = AB + BC + CD + DA = 8 + 6 + 8 + 5 = 27cm
Bài tập trắc nghiệm
Câu 1: Cho hình thang ABCD có AB = 5cm, CD = 9cm, AD = 4cm và BC = 6cm. Chu vi hình thang ABCD là:
A. 24cm
B. 26cm
C. 28cm
D. 30cm
Câu 2: Cho hình thang ABCD có chu vi là 28cm và AB = 6cm. Tính độ dài cạnh CD.
A. 4cm
B. 5cm
C. 6cm
D. 7cm
Câu 3: Cho hình thang cân ABCD có AB = 5cm, BC = 3cm và AD = 4cm. Chu vi hình thang ABCD là:
A. 16cm
B. 18cm
C. 20cm
D. 22cm
Câu 4: Cho hình thang ABCD có AB // CD, AB = 8cm, CD = 10cm, AC = 13cm. Tính độ dài cạnh BD.
A. 11cm
B. 12cm
C. 13cm
D. 14cm
Câu 5: Cho hình thang ABCD có AB // CD, AB = 4cm, CD = 6cm, BD = 3cm. Tính độ dài cạnh AC.
A. 7cm
B. 8cm
C. 9cm
D. 10cm
Tóm lại, chu vi hình thang là một công thức đơn giản nhưng hữu ích trong việc tính toán độ dài của hình thang. Việc nắm vững công thức và cách tính chu vi hình thang sẽ giúp bạn giải quyết các bài toán liên quan một cách hiệu quả và chính xác.
Chúc bạn học tốt với toanhoc.edu.vn
Bài Viết Liên Quan
Với niềm đam mê mãnh liệt đối với toán học, tôi luôn mong muốn truyền tải kiến thức và khơi gợi niềm yêu thích môn học này cho thế hệ trẻ. Tôi luôn tận tâm trong công việc giảng dạy, sử dụng phương pháp giảng dạy sáng tạo và hiệu quả để giúp học sinh tiếp thu kiến thức một cách dễ dàng và hứng thú. Với những thành tựu xuất sắc trong lĩnh vực toán học, tôi đã nhận được nhiều giải thưởng danh giá và được cộng đồng khoa học đánh giá cao. Tôi là nguồn cảm hứng và tấm gương sáng cho các thế hệ học sinh và sinh viên yêu thích toán học.