Vẽ đoạn thẳng cho biết độ dài là một kỹ năng cơ bản trong môn Toán lớp 6. Kỹ năng này giúp học sinh vẽ được các đoạn thẳng có độ dài chính xác theo yêu cầu.
Cách vẽ đoạn thẳng cho biết độ dài
Bước 1:
Chọn hai điểm A và B trên giấy.
Đo độ dài đoạn thẳng AB bằng thước kẻ.
Bước 2:
Vẽ một đường thẳng đi qua hai điểm A và B.
Bước 3:
Đánh dấu điểm C trên đường thẳng sao cho AC = độ dài đã cho.
Một số lưu ý:
- Khi vẽ đoạn thẳng, cần đảm bảo rằng hai điểm A và B nằm trên cùng một đường thẳng.
- Sử dụng thước đo chính xác để đảm bảo độ dài đoạn thẳng được vẽ đúng.
- Nối hai điểm A và C bằng một đường thẳng nét đậm.
Vẽ đoạn thẳng trên tia
Trên tia Ox để vẽ đoạn thẳng OM có độ dài bằng a ta làm như sau:
Mút O đã biết. Ta vẽ mút M như sau:
+ Đặt cạnh của thước nằm trên tia Ox sao cho vạch số 0 của thước trùng với gốc O
+ Vạch số a của thước sẽ cho ta điểm M
Đoạn thẳng OM là đoạn thẳng phải vẽ
Nhận xét: Trên tia Ox bao giờ cũng vẽ được một và chỉ một điểm m sao cho OM = a (đơn vị dài)
Cách vẽ đoạn thẳng CD bằng đoạn AB cho trước
Vẽ một tia Cy bất kì. Khi đó, ta đã biết mút C của đoạn CD. Ta vẽ mút D như sau:
+ Đặt compa sao cho một mũi nhọn trùng với mút A, mũi kia trùng với mút B của đoạn thẳng AB cho trước.
+ Giữ độ mở của compa không đổi, đặt compa sao cho một mũi nhọn trùng với gốc C của tia Cy, mũi kia nằm trên tia sẽ cho ta mút D và CD là đoạn thẳng phải vẽ.
Dấu hiệu nhận biết một điểm nằm giữa hai điểm khác
Trên tia Ox có hai điểm M và N, OM = a, ON = B, a < b thì điểm M nằm giữa hai điểm O và N.
Khi đó: ON = ON + MN
Bài tập vận dụng có lời giải chi tiết
Bài 1: Trên tia Ox, vẽ hai đoạn thẳng OM và ON sao cho OM = 3cm, ON = 6cm. Tính MN, so sánh OM và MN.
Giải:
Trên tia Ox ta có 2 điểm M, N mà OM < ON (3<6) nên điểm M nằm giữa hai điểm O và N.
Suy ra OM + MN = ON;
MN = ON – OM = 6 – 3 = 3(cm).
Vậy OM = MN = 3 (cm).
Bài 2: Trên tia Ox, vẽ ba đoạn thẳng OA, OB, OC sao cho OA = 2cm , OB = 5cm, OC = 8 cm. So sánh BC và BA.
Giải:
Ta có:
OC = 8cm; OB = 5 cm
=> OB < OC (5cm < 8 cm)
Do đó điểm B nằm giữa O và C, ta có
OB + BC = OC
=> 5 + BC = 8
=> BC = 8 – 5 = 3 (cm)
Ta có:
OA = 2cm; OB = 5cm
=> OA < OB (2cm < 5cm)
Do đó điểm A nằm giữa hai điểm O và B, ta có
OA + AB = OB
=> 2 + AB = 5
=> AB = 5 – 2 = 3 (cm)
Vậy AB = BC (=3cm)
Bài 3: Gọi A, B là hai điểm trên tia Ox. Biết OA= 8cm, AB= 2cm. Tình OB. Bài toán có mấy đáp số.
Giải:
Có hai trường hợp xảy ra:
Trường hợp 1: Điểm B và O nằm cùng phía với A
Do điểm B và O nằm cùng phía với A nên điểm B nằm giữa hai điểm A và O
Ta có: AB + BO = AO
=> 2 + OB = 8
=> OB = 8 – 2 = 6 (cm)
Vậy: OB = 6 (cm)
Trường hợp 2: Điểm B và O nằm khác phía đối với điểm A
Do điểm B và điểm O nằm về 2 phía đối với điểm A nên điểm A nằm giữa 2 điểm B và O.
Ta có OA + AB = OB
=> OB = 8 + 2 = 10 (cm)
Vậy OB = 10 (cm)
Kết luận: Bài toán có hai đáp số là 6 cm và 10 cm.
Bài 4: Cho đoạn thẳng AB dài 4 cm. Trên tia AB lấy điểm C sao cho AC =1 cm.
a) Tính CB
b) Lấy điểm D thuộc tia đối của tia BC sao cho BD=2cm. Tính CD.
Giải:
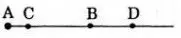
a) Trên tia AB có hai điểm C, B mà AC< AB (1cm<4cm) nên C nằm giữa hai điểm A và B.
Ta có:
AC+ CB = AB
⇒ 1+ CB = 4
⇒ CB = 3(cm)
b) Điểm D thuộc tia đối của tia BC nên điểm B nằm giữa C và D.
Ta có: CD = CB + BD = 3 + 2 = 5(cm)
Bài 5: Đoạn thẳng AC dài 5cm. Điểm B nằm giữa A và C sao cho BC= 3cm.
a) Tính AB.
b) Trên tia đối của tia BA lấy điểm D sao cho BD= 5cm. so sánh AB và CD.
Giải:
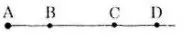
a) Điểm B nằm giữa A và C nên AB + BC = AC;
=> AB = AC – BC = 5 – 3 = 2 (cm).
b) Hai tia BC và BD trùng nhau (vì đều là tia đối của tia BA). Trên tia BC có BC< BD (3<5) nên C nằm giữa B và D.
Suy ra BC + CD = BD
=> CD = BD – BC = 5 – 3 = 2(cm).
Vậy AB = CD (= 2cm).
Với việc nắm vững kiến thức về vẽ đoạn thẳng, học sinh sẽ có nền tảng vững chắc để tiếp tục học tập các chủ đề hình học tiếp theo.
Chúc bạn học tốt với toanhoc.edu.vn
