Giá trị lượng giác của một cung - Tổng hợp công thức quan trọng

Trong toán học, lượng giác là một khái niệm quan trọng trong hình học và đặc biệt là trong lượng giác học. Lượng giác của một cung trong một đường tròn là một trong những khái niệm cơ bản mà học sinh lớp 10 thường được giới thiệu. Khám phá và hiểu biết về giá trị của lượng giác không chỉ giúp chúng ta hiểu sâu hơn về hình học mà còn áp dụng vào nhiều lĩnh vực khác trong toán học.

Giá trị lượng giác của một cung là gì?

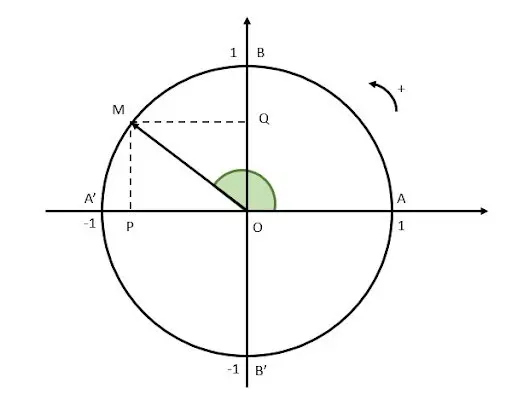
Trên đường tròn lượng giác cho cung có số đo α, tung độ y của điểm M được gọi là sin của α và kí hiệu là sinα.

Cung lượng giác: là phần của đường tròn giới hạn bởi hai điểm M và N trên đường tròn.

Góc lượng giác: là góc tạo bởi hai tia OM và ON, trong đó O là tâm đường tròn.

Đơn vị đo cung và góc lượng giác:

• Độ (°): 1 vòng tròn đầy có số đo 360°.
• Radian (rad): 1 vòng tròn đầy có số đo 2π rad.

Hệ quả của giá trị lượng giác của một cung

Tính tuần hoàn

• \(Sin(α + 2πk) = Sinα, ∀k ∈ Z\)
• \(Cos(α + 2πk) = Cosα, ∀k ∈ Z\)

• \(Tan(α + πk) = Tanα, ∀k ∈ Z\)
• \(Cot(α + πk) = Cotα, ∀k ∈ Z\)

Tính chẵn lẻ

• \(Sin(-α) = -Sinα.\)
• \(Cos(-α) = Cosα.\)
• \(Tan(-α) = -Tanα.\)
• \(Cot(-α) = -Cotα.\)

Công thức cộng

• \(Sin(α + β) = SinαCosβ + CosαSinβ.\)
• \(Cos(α + β) = CosαCosβ – SinαSinβ.\)
• \(Tan(α + β) = (Tanα + Tanβ)/(1 – TanαTanβ).\)
• \(Cot(α + β) = (CotαCotβ – 1)/(Cotα + Cotβ).\)

Công thức nhân đôi

• \(Sin2α = 2SinαCosα.\)
• \(Cos2α = Cos^2α – Sin^2α = 2Cos^2α – 1 = 1 – 2Sin^2α.\)
• \(Tan2α = Sin^2α/(Cos^2α) = (1 – Cos^2α)/Cos^2α.\)
• \(Cot2α = Cos^2α/Sin^2α = (1 – Sin^2α)/Sin^2α.\)

Hệ quả khác

• Công thức biến đổi:
  • \(Sinα + Sinβ = 2Sin((α + β)/2)Cos((α – β)/2).\)
  • \(Sinα – Sinβ = 2Cos((α + β)/2)Sin((α – β)/2).\)
  • \(Cosα + Cosβ = 2Cos((α + β)/2)Cos((α – β)/2).\)
  • \(Cosα – Cosβ = -2Sin((α + β)/2)Sin((α – β)/2).\)
• Công thức cộng và trừ tang:
  • \(Tanα + Tanβ = Sin(α + β)/CosαCosβ.\)
  • \(Tanα – Tanβ = Sin(α – β)/CosαCosβ.\)
• Công thức cộng và trừ cotang:
  • \(Cotα + Cotβ = Cos(α + β)/SinαSinβ.\)
  • \(Cotα – Cotβ = -Cos(α – β)/SinαSinβ.\)

Quan hệ giữa các giá trị lượng giác

Công thức lượng giác cơ bản

\(\[
\sin^2 \alpha + \cos^2 \alpha = 1
\]

\[
\tan \alpha = \frac{\sin \alpha}{\cos \alpha}, \quad \alpha \neq \frac{\pi}{2} + k\pi, \quad k \in \mathbb{Z}
\]

\[
\cot \alpha = \frac{\cos \alpha}{\sin \alpha}, \quad \alpha \neq k\pi, \quad k \in \mathbb{Z}
\]

\[
\tan \alpha \cdot \cot \alpha = 1, \quad \alpha \neq \frac{k\pi}{2}, \quad k \in \mathbb{Z}
\]

\[
1 + \tan^2 \alpha = \frac{1}{\cos^2 \alpha}, \quad \alpha \neq \frac{\pi}{2} + k\pi, \quad k \in \mathbb{Z}
\]

\[
1 + \cot^2 \alpha = \frac{1}{\sin^2 \alpha}, \quad \alpha \neq k\pi, \quad k \in \mathbb{Z}
\]\)

Giá trị lượng giác của các cung có liên quan đặc biệt

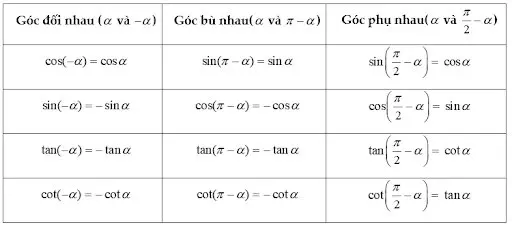
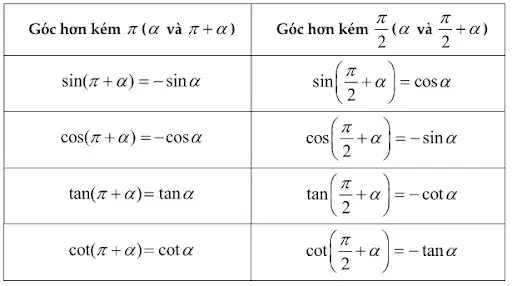
Chú ý: Để nhớ nhanh các công thức trên ta nhớ câu: ” cos – đối, sin – bù, phụ – chéo, hơn kém  tang côtang, hơn kém 2  chéo sin”. Với nguyên tắc nhắc đến giá trị nào thì nó bằng còn không nhắc thì đối.

Các dạng toán giá trị lượng giác của một cung

Tính giá trị lượng giác của một cung khi biết số đo của cung

Ví dụ:

• Tính sinα, cosα, tanα, cotα biết α = 30°.
• Tính sin(α + 180°), cos(α + 90°), tan(α – 90°), cot(α + 270°) biết α = 45°.

Tìm cung có giá trị lượng giác cho trước

Ví dụ:

• Tìm α (0° ≤ α ≤ 360°) biết sinα = 0,5.
• Tìm α (0° ≤ α ≤ 360°) biết cosα = -0,8.

Chứng minh đẳng thức lượng giác

Ví dụ:

• Chứng minh \(sin^2α + cos^2α = 1.\)
• Chứng minh \(tanα + cotα = cos^2α/sinα.\)

Bài tập có lời giải

Cho \(\frac{\pi}{2} < \alpha < \pi\). Xác định dấu của các biểu thức sau:

1. a) \(\sin\left(\frac{\pi}{2} + \alpha\right)\)
2. b) \(\tan\left(\frac{3\pi}{2} – \alpha\right)\)
3. c) \(\cos\left(-\frac{\pi}{2} + \alpha\right) \cdot \tan(\pi – \alpha)\)
4. d) \(\sin\left(\frac{14\pi}{9}\right) \cdot \cot(\pi + \alpha)\)

Lời giải

1. a) Ta có \(\frac{\pi}{2} < \alpha < \pi \Rightarrow -\frac{\pi}{2} < \frac{\pi}{2} + \alpha < \frac{3\pi}{2} – \frac{\pi}{2} < \sin\left(\frac{\pi}{2} + \alpha\right) < 0\)
2. b) Ta có \(-\frac{\pi}{2} < -\alpha < -\frac{\pi}{2} \Rightarrow 0 < \frac{3\pi}{2} – \alpha < \pi – \frac{\pi}{2} \Rightarrow \tan\left(\frac{3\pi}{2} – \alpha\right) < 0\)
3. c) Ta có \(\frac{\pi}{2} < \alpha < \pi \Rightarrow 0 < -\frac{\pi}{2} + \alpha < \frac{\pi}{2} \Rightarrow \cos\left(-\frac{\pi}{2} + \alpha\right) > 0\)

Và \(0 < \pi – \alpha < \frac{\pi}{2} \Rightarrow \tan(\pi + \alpha) > 0\)

Vậy \(\cos\left(-\frac{\pi}{2} + \alpha\right) \cdot \tan(\pi – \alpha) > 0\)

1. d) Ta có \(\frac{3\pi}{2} < \frac{14\pi}{9} < 2\pi \Rightarrow \sin\left(\frac{14\pi}{9}\right) < 0\)

\(\frac{\pi}{2} < \alpha < \pi \Rightarrow \frac{3\pi}{2} < \pi + \alpha < 2\pi$ suy ra $\cot(\pi + \alpha) < 0\)

Vậy \(\sin\left(\frac{14\pi}{9}\right) \cdot \cot(\pi + \alpha) > 0\)

Bài tập trắc nghiệm bài giá trị lượng giác của một cung 

Câu 1: Cho cung α có số đo 120°. Giá trị cosα là:

1. √3/2 B. -√3/2 C. 1/2 D. -1/2

Câu 2: Cho cung α có số đo 300°. Giá trị sinα là:

1. 1/2 B. -1/2 C. √3/2 D. -√3/2

Câu 3: Cho tanα = 3. Giá trị cotα là:

1. 1/3 B. -1/3 C. 3 D. -3

Câu 4: Cho sinα = √2/2. Giá trị cosα là:

1. √2/2 B. -√2/2 C. 1/2 D. -1/2

Câu 5: Cho α và β là hai cung có cùng số đo. Giá trị sinα + cosβ là:

1. 0 B. 1 C. -1 D. √2

Câu 6: Cho α và β là hai cung có cùng số đo. Giá trị tanα – cotβ là:

1. 0 B. 1 C. -1 D. √2

Câu 7: Chọn khẳng định sai:

1. sin(-α) = -sinα B. cos(-α) = cosα C. tan(-α) = tanα D. cot(-α) = cotα

Câu 8: Chọn khẳng định đúng:

1. sin(α + π) = sinα B. cos(α + π) = cosα C. tan(α + π) = tanα D. cot(α + π) = cotα

Câu 9: Chọn khẳng định đúng:

1. sin(α + 2π) = sinα B. cos(α + 2π) = cosα C. tan(α + 2π) = tanα D. cot(α + 2π) = cotα

Câu 10: Chọn khẳng định đúng:

1. sin(α + π/2) = cosα B. cos(α + π/2) = -sinα C. tan(α + π/2) = cotα D. cot(α + π/2) = tanα

Đáp án:

1. A
2. D
3. A
4. A
5. A
6. D
7. C
8. B
9. A
10. A

Giải thích:

• Sử dụng định nghĩa, hệ thức lượng giác và giá trị lượng giác của các cung đặc biệt để giải các câu hỏi.
• Lưu ý các tính chất chẵn lẻ, tuần hoàn của giá trị lượng giác.

Bài viết này đã cung cấp cho bạn kiến thức nền tảng về giá trị lượng giác của một cung. 

Chúc bạn học tốt