Diện tích xung quanh của hình lăng trụ đứng là một chủ đề quan trọng trong chương trình Toán lớp 8. Bài viết này sẽ cung cấp cho bạn đầy đủ kiến thức về diện tích xung quanh của hình lăng trụ đứng, bao gồm định nghĩa, công thức tính, các dạng toán thường gặp và bài tập minh họa.
Hình lăng trụ đứng là gì?
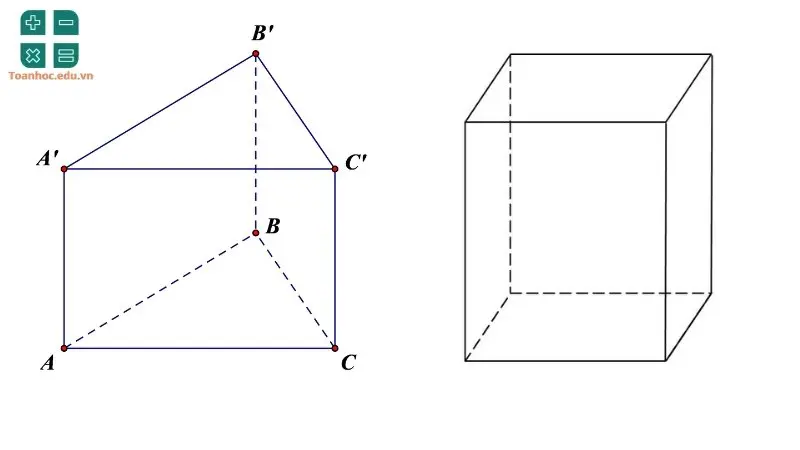
Hình lăng trụ đứng có hai đáy là những đa giác, các mặt bên là những hình chữ nhật.
Các mặt phẳng chứa đáy của hình lăng trụ đứng là các mặt phẳng song song, các mặt bên vuông góc với hai mặt phẳng đáy, các cạnh bên vuông góc với hai mặt phẳng đáy. Độ dài một cạnh bên gọi là chiều cao.
Hình lăng trụ đứng có đáy là hình bình hành gọi là hình hộp đứng.
Diện tích xung quanh của hình lăng trụ đứng
Diện tích xung quanh của hình lăng trụ đứng là tổng diện tích của các mặt bên.
Công thức:
S_xq = Chu vi đáy x Chiều cao
\(S_{xq} = C_d.h\)
trong đó:
S_xq là diện tích xung quanh
C_d là chu vi đáy
h là chiều cao
Ví dụ:
Cho hình lăng trụ đứng tam giác ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, AB = 3cm, AC = 4cm, AA’ = 5cm.
Tính diện tích xung quanh của hình lăng trụ đứng.
Chu vi đáy ABC là:
C_d = AB + AC + BC = 3cm + 4cm + 5cm = 12cm
Diện tích xung quanh của hình lăng trụ đứng là:
\(S_{xq} = C_d.h\) = 12cm x 5cm = 60cm²
Các dạng toán thường gặp về diện tích xung quanh của hình lăng trụ đứng
Dạng 1: Tính diện tích xung quanh của hình lăng trụ đứng khi biết chu vi đáy và chiều cao.
Ví dụ:
Cho hình lăng trụ đứng tam giác ABC.A’B’C’ có đáy ABC là tam giác đều với cạnh AB = 4cm, AA’ = 5cm. Diện tích xung quanh của hình lăng trụ là:
Sxq = Chu vi đáy x Chiều cao = (AB + AC + BC) x AA’ = (4cm + 4cm + 4cm) x 5cm = 60cm²
Dạng 2: Tính chu vi đáy hoặc chiều cao khi biết diện tích xung quanh và một trong hai đại lượng kia.
Ví dụ:
Một hình lăng trụ đứng tam giác có diện tích xung quanh là 90cm² và chiều cao là 10cm. Chu vi đáy của hình lăng trụ là bao nhiêu?
Chu vi đáy = Diện tích xung quanh / Chiều cao = 90cm² / 10cm = 9cm
Dạng 3: Vận dụng tính diện tích xung quanh vào giải bài toán thực tế.
Ví dụ:
Một hộp gỗ hình lăng trụ đứng tứ giác có đáy là hình chữ nhật với chiều dài 5cm, chiều rộng 4cm, chiều cao của hộp là 6cm. Người ta muốn sơn toàn bộ mặt ngoài của hộp gỗ. Diện tích phần cần sơn là bao nhiêu?
Diện tích xung quanh của hộp gỗ là:
Sxq = Chu vi đáy x Chiều cao = (5cm + 4cm + 5cm + 4cm) x 6cm = 108cm²
Diện tích phần cần sơn là:
108cm² + 2 x (5cm x 4cm) = 148cm²
Bài tập có lời giải trong sách giáo khoa
Bài 1 (SGK Toán 8, tập 2, trang 111)
Cho hình lăng trụ đứng tam giác ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, AB = 6cm, AC = 8cm, AA’ = 10cm.
a) Tính diện tích xung quanh của hình lăng trụ.
b) Tính diện tích toàn phần của hình lăng trụ.
Lời giải:
a) Diện tích xung quanh của hình lăng trụ là:
Sxq = Chu vi đáy x Chiều cao = (AB + AC + BC) x AA’ = (6cm + 8cm + 10cm) x 10cm = 240cm²
b) Diện tích hai mặt đáy là:
\(S_{\text{đáy}} = 2 \times \left(\frac{1}{2} \times AB \times AC\right) = 2 \times \left(\frac{1}{2} \times 6 \, \text{cm} \times 8 \, \text{cm}\right) = 48 \, \text{cm}^2\)Diện tích toàn phần của hình lăng trụ là:
Stp = Sxq + 2 x Sđáy = 240cm² + 2 x 48cm² = 336cm²
Bài 2 (SGK Toán 8, tập 2, trang 111)
Một hình lăng trụ đứng tứ giác ABCD.EFGH có đáy ABCD là hình chữ nhật với AB = 5cm, BC = 4cm, chiều cao AA’ = 6cm.
a) Tính diện tích xung quanh của hình lăng trụ.
b) Tính diện tích toàn phần của hình lăng trụ.
Lời giải:
a) Diện tích xung quanh của hình lăng trụ là:
Sxq = Chu vi đáy x Chiều cao = (AB + BC + CD + DA) x AA’ = (5cm + 4cm + 5cm + 4cm) x 6cm = 108cm²
b) Diện tích hai mặt đáy là:
Sđáy = 2 x (AB x BC) = 2 x (5cm x 4cm) = 40cm²
Diện tích toàn phần của hình lăng trụ là:
Stp = Sxq + 2 x Sđáy = 108cm² + 2 x 40cm² = 188cm²
Bài viết đã cung cấp cho bạn đầy đủ kiến thức về diện tích xung quanh của hình lăng trụ đứng. Hy vọng những thông tin này hữu ích cho bạn và giúp bạn giải quyết tốt các bài toán liên quan đến diện tích xung quanh của hình lăng trụ đứng.
Chúc bạn học tốt với toanhoc.edu.vn
