Thể tích khối lập phương là một khái niệm quan trọng trong toán học, được ứng dụng trong nhiều lĩnh vực như xây dựng, cơ khí, kiến trúc… Bài viết này sẽ giới thiệu về khái niệm thể tích khối lập phương, công thức tính thể tích và một số ứng dụng của nó.
Lý thuyết khối lập phương
Khối lập phương là một hình đa diện có 6 mặt, 8 đỉnh và 12 cạnh bằng nhau. Các mặt của khối lập phương là những hình vuông.
Thể tích của khối lập phương là thể tích của phần không gian được giới hạn bởi 6 mặt của khối lập phương.
Công thức tính thể tích khối lập phương
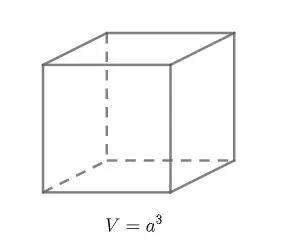
V = a³
trong đó:
V là thể tích của khối lập phương.
a là độ dài cạnh của khối lập phương.
Ví dụ:
Cho một khối lập phương có cạnh a = 3cm. Thể tích của khối lập phương là:
V = a³ = 3³ = 27 cm³
Tính thể tích khối lập phương dựa vào diện tích một mặt
V = S.h
trong đó:
V là thể tích của khối lập phương.
S là diện tích một mặt của khối lập phương.
h là độ dài đường cao của khối lập phương (bằng độ dài cạnh của khối lập phương).
Tính thể tích khối lập phương dựa vào diện tích đáy
V = B.h
trong đó:
V là thể tích của khối lập phương.
B là diện tích đáy của khối lập phương.
h là chiều cao của khối lập phương (bằng độ dài cạnh của khối lập phương).
Các dạng bài tập về thể tích khối lập phương
Dạng 1: Tính thể tích khối lập phương khi biết độ dài cạnh.
Ví dụ:
Cho một khối lập phương có cạnh là 5cm. Tính thể tích của khối lập phương đó.
Bài giải:
Thể tích của khối lập phương là:
V = a³ = 5³ = 125 cm³
Dạng 2: Tính độ dài cạnh của khối lập phương khi biết thể tích.
Ví dụ:
Một khối lập phương có thể tích là 216 cm³. Tính độ dài cạnh của khối lập phương đó.
Bài giải:
Gọi cạnh của khối lập phương là a.
Ta có: V = a³ = 216 cm³
⇔ a³ = 6³
⇔ a = 6 cm
Dạng 3: Tính diện tích toàn phần của khối lập phương khi biết thể tích.
Ví dụ:
Một khối lập phương có thể tích là 64 cm³. Tính diện tích toàn phần của khối lập phương đó.
Bài giải:
Gọi cạnh của khối lập phương là a.
Ta có: V = a³ = 64 cm³
⇔ a³ = 4³
⇔ a = 4 cm
Diện tích toàn phần của khối lập phương là:
S = 6a² = 6.4² = 96 cm²
Dạng 4: Tính các đại lượng liên quan khác của khối lập phương (chiều cao, đường chéo…)
Ví dụ:
Cho một khối lập phương có cạnh là 3cm. Tính đường chéo của khối lập phương đó.
Bài giải:
Gọi cạnh của khối lập phương là a và đường chéo của khối lập phương là d.
Ta có: d² = a² + a² + a²
⇔ d² = 3a²
⇔ d = a√3
⇔ d = 3√3 cm
Ngoài ra, còn có một số dạng bài tập nâng cao về thể tích khối lập phương như:
Tính thể tích của một khối đa diện được ghép bởi các khối lập phương.
Tính thể tích của một phần của khối lập phương.
Bài tập về thể tích khối lập phương
Bài 1:
Cho một khối lập phương có cạnh là 4cm. Tính thể tích của khối lập phương đó.
Bài 2:
Một khối lập phương có thể tích là 27 cm³. Tính độ dài cạnh của khối lập phương đó.
Bài 3:
Một khối lập phương có diện tích toàn phần là 96 cm². Tính thể tích của khối lập phương đó.
Bài 4:
Cho một khối lập phương có cạnh là 5cm. Tính đường chéo của khối lập phương đó.
Bài 5:
Một khối gỗ hình lập phương có cạnh là 3cm. Người ta cắt đi một phần khối gỗ hình lập phương theo một mặt phẳng vuông góc với một cạnh, cách đỉnh 1cm. Tính thể tích phần gỗ còn lại.
Hướng dẫn giải bài tập
Bài 1:
Lời giải:
Thể tích của khối lập phương là:
V = a³ = 4³ = 64 cm³
Bài 2:
Lời giải:
Gọi cạnh của khối lập phương là a.
Ta có: V = a³ = 27 cm³
⇔ a³ = 3³
⇔ a = 3 cm
Bài 3:
Lời giải:
Gọi cạnh của khối lập phương là a.
Ta có: S = 6a² = 96 cm²
⇔ a² = 16 cm²
⇔ a = 4 cm
Thể tích của khối lập phương là:
V = a³ = 4³ = 64 cm³
Bài 4:
Lời giải:
Gọi cạnh của khối lập phương là a và đường chéo của khối lập phương là d.
Ta có: d² = a² + a² + a²
⇔ d² = 3a²
⇔ d = a√3
⇔ d = 5√3 cm
Bài 5:
Lời giải:
Phần gỗ còn lại có dạng hình hộp chữ nhật với kích thước:
Chiều dài: 3cm – 1cm = 2cm
Chiều rộng: 3cm
Chiều cao: 3cm
Thể tích phần gỗ còn lại là:
V = lwh = 2.3.3 = 18 cm³
Bài tập trắc nghiệm về thể tích khối lập phương có đáp án
Câu 1:
Cho một khối lập phương có cạnh a = 5cm. Thể tích của khối lập phương là:
A. 125 cm³
B. 250 cm³
C. 375 cm³
D. 500 cm³
Câu 2:
Một khối lập phương có thể tích là 216 cm³. Độ dài cạnh của khối lập phương là:
A. 4 cm
B. 5 cm
C. 6 cm
D. 7 cm
Câu 3:
Cho một khối lập phương có cạnh a. Diện tích toàn phần của khối lập phương là:
A. 6a²
B. 4a²
C. 8a²
D. 12a²
Câu 4:
Một khối lập phương có diện tích toàn phần là 384 cm². Độ dài cạnh của khối lập phương là:
A. 4 cm
B. 5 cm
C. 6 cm
D. 7 cm
Câu 5:
Cho một khối lập phương có cạnh a. Thể tích của khối lập phương tăng gấp 8 lần khi cạnh a tăng lên:
A. 2 lần
B. 3 lần
C. 4 lần
D. 5 lần
Câu 6:
Một khối lập phương có thể tích là 64 cm³. Cạnh của khối lập phương sau khi tăng gấp đôi là:
A. 4 cm
B. 5 cm
C. 6 cm
D. 7 cm
Câu 7:
Cho một khối lập phương có cạnh a. Đường chéo của một mặt của khối lập phương là:
A. a√2
B. a√3
C. a√4
D. a√5
Câu 8:
Một khối lập phương có đường chéo của một mặt là 6√2 cm. Cạnh của khối lập phương là:
A. 4 cm
B. 5 cm
C. 6 cm
D. 7 cm
Câu 9:
Cho một khối lập phương có cạnh a. Đường chéo của khối lập phương là:
A. a√3
B. a√2
C. a√4
D. a√5
Câu 10:
Một khối lập phương có đường chéo là 10√3 cm. Cạnh của khối lập phương là:
A. 4 cm
B. 5 cm
C. 6 cm
D. 7 cm
Đáp án:
- A
- A
- A
- B
- C
- B
- A
- B
- A
- B
Như vậy, bài viết này đã giới thiệu về khái niệm thể tích khối lập phương, công thức tính thể tích và một số ứng dụng của nó. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức bổ ích về thể tích khối lập phương.
Chúc bạn học tốt với toanhoc.edu.vn
