Lý thuyết và công thức thể tích hình hộp chữ nhật

Thể tích hình hộp chữ nhậtlà một hình khối quen thuộc trong đời sống, được ứng dụng trong nhiều lĩnh vực như xây dựng, kiến trúc, cơ khí,… Hiểu rõ về thể tích của hình hộp chữ nhật là điều cần thiết để giải quyết các bài toán liên quan đến hình khối này.

Hình hộp chữ nhật và thể tích hình hộp chữ nhật

Hình hộp chữ nhật là hình có 6 mặt, 8 đỉnh và 12 cạnh. Các mặt đối diện của hình hộp chữ nhật bằng nhau và vuông góc với nhau.

Thể tích hình hộp chữ nhật là lượng không gian được giới hạn bởi 6 mặt của hình hộp chữ nhật.

Công thức tính thể tích hình hộp chữ nhật

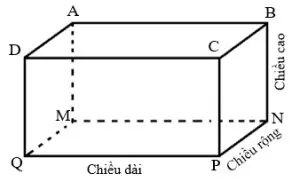
V = a × b × c

Trong đó:

V là thể tích hình hộp chữ nhật (cm³)

a, b, c là ba kích thước của hình hộp chữ nhật (cm)

Ví dụ:

Cho một hình hộp chữ nhật có chiều dài a = 5 cm, chiều rộng b = 4 cm và chiều cao c = 3 cm. Thể tích của hình hộp chữ nhật là:

V = a × b × c = 5 × 4 × 3 = 60 cm³

Đơn vị đo thể tích hình hộp chữ nhật

Đơn vị cơ bản: cm³

Đơn vị khác: dm³, m³, lít

Các dạng bài tập và phương pháp giải bài tập thể tích hình hộp chữ nhật

Dạng 1: Cho ba kích thước của hình hộp chữ nhật, tính thể tích của hình hộp chữ nhật.

Phương pháp giải:

Áp dụng công thức V = a × b × c, trong đó a, b, c là ba kích thước của hình hộp chữ nhật.

Đơn vị đo của V phải phù hợp với đơn vị đo của a, b, c.

Ví dụ:

Cho một hình hộp chữ nhật có chiều dài a = 5 cm, chiều rộng b = 4 cm và chiều cao c = 3 cm. Tính thể tích của hình hộp chữ nhật.

Giải:

Thể tích của hình hộp chữ nhật là:

V = a × b × c = 5 × 4 × 3 = 60 cm³

Dạng 2: Cho diện tích xung quanh hoặc diện tích toàn phần của hình hộp chữ nhật và một kích thước, tính thể tích của hình hộp chữ nhật.

Phương pháp giải:

Bước 1: Tính chu vi đáy của hình hộp chữ nhật.

Bước 2: Tính hai kích thước còn lại của hình hộp chữ nhật.

Bước 3: Tính thể tích của hình hộp chữ nhật.

Ví dụ:

Một hình hộp chữ nhật có diện tích xung quanh Sxq = 250 cm² và chiều cao h = 5 cm. Tính chu vi đáy và thể tích của hình hộp chữ nhật.

Giải:

Bước 1: Chu vi đáy của hình hộp chữ nhật là:

C = Sxq/h = 250/5 = 50 cm

Bước 2: Gọi chiều dài và chiều rộng của hình hộp chữ nhật lần lượt là a và b. Ta có:

2a + 2b = 50

Bước 3: Tính a và b. Ví dụ, ta chọn a = 20 cm, b = 10 cm.

Bước 4: Tính thể tích của hình hộp chữ nhật:

V = a × b × c = 20 × 10 × 5 = 1000 cm³

Dạng 3: Cho các dữ liệu liên quan đến thể tích của hình hộp chữ nhật, tìm kích thước của hình hộp chữ nhật.

Phương pháp giải:

Bước 1: Lập phương trình liên hệ giữa các dữ liệu và kích thước của hình hộp chữ nhật.

Bước 2: Giải phương trình để tìm kích thước của hình hộp chữ nhật.

Ví dụ:

Một bể nước dạng hình hộp chữ nhật có chiều dài gấp đôi chiều rộng và chiều cao là 1,5 m. Bể chứa được 1800 lít nước. Tính kích thước của bể nước.

Giải:

Bước 1: Gọi chiều rộng của bể nước là x (m). Ta có:

Chiều dài của bể nước là 2x (m).

Thể tích của bể nước là: V = x × 2x × 1,5 = 3x² (m³).

Bước 2: Đổi 1800 lít sang đơn vị m³:

1800 lít = 1800 dm³ = 1,8 m³.

Bước 3: Lập phương trình:

3x² = 1,8

Bước 4: Giải phương trình:

x² = 0,6

x = √0,6 ≈ 0,775

Bước 5: Tính kích thước của bể nước:

Chiều rộng: x ≈ 0,775 m

Chiều dài: 2x ≈ 1,55 m

Chiều cao: 1,5 m

Bài tập có lời giải về thể tích hình hộp chữ nhật

Bài tập 1: Một hình hộp chữ nhật có chiều dài a = 6 cm, chiều rộng b = 5 cm và chiều cao c = 4 cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình hộp chữ nhật.

Lời giải:

Diện tích xung quanh:

Sxq = 2h(a + b) = 2 × 4 × (6 + 5) = 88 cm²

Diện tích toàn phần:

Stp = 2(ab + ac + bc) = 2(6 × 5 + 6 × 4 + 5 × 4) = 154 cm²

Thể tích:

V = a × b × c = 6 × 5 × 4 = 120 cm³

Bài tập 2: Một hình hộp chữ nhật có diện tích xung quanh Sxq = 250 cm² và chiều cao h = 5 cm. Tính chu vi đáy và thể tích của hình hộp chữ nhật.

Lời giải:

Chu vi đáy:

C = Sxq/h = 250/5 = 50 cm

Nửa chu vi đáy:

C/2 = 50/2 = 25 cm

Gọi chiều dài và chiều rộng của hình hộp chữ nhật lần lượt là a và b:

a + b = 25

Ta có thể chọn a = 15 cm và b = 10 cm.
Thể tích của hình hộp chữ nhật:
V = a × b × c = 15 × 10 × 5 = 750 cm³

Bài tập 3: Một bể nước dạng hình hộp chữ nhật có chiều dài gấp đôi chiều rộng và chiều cao là 1,5 m. Bể chứa được 1800 lít nước. Tính kích thước của bể nước.

Lời giải:

Gọi chiều rộng của bể nước là x (m).
Chiều dài của bể nước là 2x (m).
Thể tích của bể nước:
V = x × 2x × 1,5 = 3x² (m³)

Đổi 1800 lít sang đơn vị m³:

1800 lít = 1800 dm³ = 1,8 m³

Lập phương trình:

3x² = 1,8

Giải phương trình:

x² = 0,6

x = √0,6 ≈ 0,775

Kích thước của bể nước:

Chiều rộng: x ≈ 0,775 m

Chiều dài: 2x ≈ 1,55 m

Chiều cao: 1,5 m

Bài tập tự luận về thể tích hình hộp chữ nhật

Bài tập 1: Một hình hộp chữ nhật có chiều dài 8 cm, chiều rộng 5 cm và chiều cao 7 cm. Tính:

Diện tích xung quanh

Diện tích toàn phần

Thể tích

Bài tập 2: Một hình hộp chữ nhật có diện tích xung quanh là 376 cm² và chiều cao là 8 cm. Tính:

Chu vi đáy

Diện tích đáy

Thể tích

Bài tập 3: Một bể nước dạng hình hộp chữ nhật có chiều dài 2 m, chiều rộng 1,5 m và chiều cao 1 m. Bể chứa đầy nước. Người ta mở vòi cho nước chảy ra, mỗi phút chảy được 20 lít. Sau 45 phút, lượng nước còn lại trong bể chiếm 2/5 thể tích bể. Hỏi lúc đầu bể chứa bao nhiêu lít nước?

Bài tập 4: Một hộp đựng quà có dạng hình hộp chữ nhật với kích thước đáy là 20 cm x 15 cm và chiều cao là 12 cm. Người ta muốn dán giấy màu xung quanh và bên trong hộp quà (trừ mặt đáy). Tính diện tích giấy màu cần dùng.

Bài tập 5: Một khối gỗ hình hộp chữ nhật có chiều dài 1,2 m, chiều rộng 8 dm và chiều cao 60 cm. Người ta cắt đi một khối gỗ hình hộp chữ nhật nhỏ hơn có chiều dài 60 cm, chiều rộng 4 dm và chiều cao 30 cm. Tính thể tích phần gỗ còn lại.

Bài tập trắc nghiệm về thể tích hình hộp chữ nhật

Câu 1:Một hình hộp chữ nhật có chiều dài 8 cm, chiều rộng 5 cm và chiều cao 7 cm. Thể tích của hình hộp chữ nhật là:

A. 280 cm³

B. 290 cm³

C. 300 cm³

D. 310 cm³

Câu 2:Một hình hộp chữ nhật có diện tích xung quanh là 376 cm² và chiều cao là 8 cm. Chu vi đáy của hình hộp chữ nhật là:

A. 47 cm

B. 48 cm

C. 49 cm

D. 50 cm

Câu 3:Một bể nước dạng hình hộp chữ nhật có chiều dài 2 m, chiều rộng 1,5 m và chiều cao 1 m. Bể chứa đầy nước. Người ta mở vòi cho nước chảy ra, mỗi phút chảy được 20 lít. Sau 45 phút, lượng nước còn lại trong bể chiếm 2/5 thể tích bể. Lúc đầu bể chứa bao nhiêu lít nước?

A. 2400 lít

B. 2500 lít

C. 2600 lít

D. 2700 lít

Câu 4:Một hộp đựng quà có dạng hình hộp chữ nhật với kích thước đáy là 20 cm x 15 cm và chiều cao là 12 cm. Người ta muốn dán giấy màu xung quanh và bên trong hộp quà (trừ mặt đáy). Diện tích giấy màu cần dùng là:

A. 900 cm²

B. 950 cm²

C. 1000 cm²

D. 1050 cm²

Câu 5:Một khối gỗ hình hộp chữ nhật có chiều dài 1,2 m, chiều rộng 8 dm và chiều cao 60 cm. Người ta cắt đi một khối gỗ hình hộp chữ nhật nhỏ hơn có chiều dài 60 cm, chiều rộng 4 dm và chiều cao 30 cm. Tính thể tích phần gỗ còn lại.

A. 43200 cm³

B. 43300 cm³

C. 43400 cm³

D. 43500 cm³

Câu 6:Một hình hộp chữ nhật có diện tích toàn phần là 600 cm² và chiều cao là 10 cm. Chu vi đáy của hình hộp chữ nhật là:

A. 30 cm

B. 32 cm

C. 34 cm

36 cm

Câu 7:Một bể cá dạng hình hộp chữ nhật có chiều dài 1 m, chiều rộng 70 cm và chiều cao 60 cm. Mực nước trong bể cao 30 cm. Người ta cho vào bể một hòn đá thì thể tích tăng 14000 cm³. Hỏi mực nước trong bể lúc này cao bao nhiêu?

A. 40 cm

B. 42 cm

C. 44 cm

D. 46 cm

Câu 8:Một chiếc hộp hình lập phương không có nắp được sơn cả mặt trong và mặt ngoài. Diện tích phải sơn tổng cộng là 1440 cm². Tính thể tích của hình lập phương đó.

A. 512 cm³

B. 518 cm³

C. 524 cm³

D. 530 cm³

Câu 9:Một hình hộp chữ nhật có chiều dài 5 cm, chiều rộng 4 cm và chiều cao 3 cm. Thể tích của một hình lập phương có cạnh bằng trung bình cộng ba kích thước của hình hộp chữ nhật là:

A. 64 cm³

B. 68 cm³

C. 72 cm³

D. 76 cm³

Câu 10:Một khối kim loại hình hộp chữ nhật có chiều dài 9 cm, chiều rộng 5 cm, chiều cao 11 cm. Khối kim loại đó nặng 1,98 kg. Hỏi 1 cm³ kim loại đó nặng bao nhiêu gam?

A. 6,5 gam

B. 6,6 gam

C. 6,7 gam

D. 6,8 gam

Hy vọng bài viết này đã cung cấp cho các bạn những kiến thức cần thiết về thể tích hình hộp chữ nhật.