Lý thuyết hình thang - Toán học lớp 8

Hình thang là một tứ giác có một cặp cạnh đối song song. Hình thang có nhiều dạng khác nhau như hình thang vuông, hình thang cân,… Hình thang được ứng dụng trong nhiều lĩnh vực như kiến trúc, xây dựng, thiết kế,…Đây là một chủ đề quan trọng trong chương trình Toán học lớp 8, được học ở phần Hình học.

Định nghĩa hình thang 

Hình thang là một loại hình tứ giác có ít nhất một cặp cạnh đối song song với nhau. Các cạnh song song này được gọi là các đáy của hình thang, trong khi hai cạnh còn lại, không nhất thiết phải song song, được gọi là các cạnh bên. Hình thang là một trong những dạng cơ bản của hình tứ giác và có một số tính chất đặc biệt liên quan đến cấu trúc và góc của nó.

Phân loại hình thang

Hình thang có thể được phân loại dựa trên các tính chất của cạnh và góc thành các loại sau:

Hình thang thường (Hình thang đơn giản):

• Định nghĩa: Hình thang thường là hình tứ giác có một cặp cạnh đối song song, được gọi là cạnh đáy, trong khi cặp cạnh còn lại không song song.
• Tính chất: Trong hình thang thường, không có tính chất đặc biệt nào về độ dài cạnh hay góc ngoài việc có một cặp cạnh song song.

Hình thang cân:

• Định nghĩa: Hình thang cân là hình thang mà hai cạnh bên không song song có độ dài bằng nhau.
• Tính chất: Trong hình thang cân, các góc kề một đáy bằng nhau. Điều này cũng có nghĩa là các góc kề đáy còn lại cũng bằng nhau. Đường chéo trong hình thang cân có độ dài bằng nhau.

Hình thang vuông:

• Định nghĩa: Hình thang vuông là hình thang có ít nhất một góc vuông. Trong hình thang vuông, thường có một hoặc hai góc tại chân cạnh bên là góc vuông.
• Tính chất: Hình thang vuông kết hợp tính chất của hình thang với tính chất của các góc vuông, làm cho việc tính toán diện tích và chu vi trở nên dễ dàng hơn trong một số trường hợp.

Mỗi loại hình thang có những ứng dụng và tính chất riêng biệt, phù hợp với nhu cầu và mục đích sử dụng khác nhau trong thực tế và hình học.

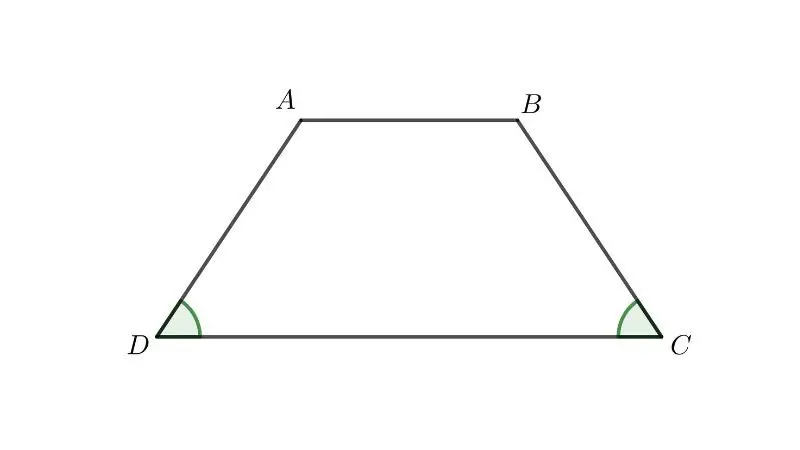
Tính chất hình thang

Hình thang là một loại hình tứ giác với ít nhất một cặp cạnh đối song song. Tính chất của hình thang bao gồm những điểm chính sau đây:

Cạnh đáy: Hình thang có ít nhất một cặp cạnh đối song song, được gọi là cạnh đáy. Trong trường hợp cả hai cặp cạnh đối đều song song, hình thang trở thành một hình bình hành.

Cạnh bên: Hai cạnh không song song của hình thang được gọi là cạnh bên.

Góc: Trong hình thang, các góc ở cùng một phía của một cạnh bên không nhất thiết phải bằng nhau, trừ khi đó là hình thang cân.

Đường chéo: Đường chéo của hình thang nối hai đỉnh đối diện và không nhất thiết phải bằng nhau hoặc vuông góc.

Đường trung bình: Đường trung bình của hình thang là đoạn thẳng nối trung điểm của hai cạnh bên. Đặc tính quan trọng của đường trung bình là nó song song với hai cạnh đáy và có độ dài bằng nửa tổng độ dài của hai cạnh đáy.

Tính chất riêng của hình thang cân:

• Hình thang cân có hai cạnh bên bằng nhau.
• Các góc kề một cạnh đáy của hình thang cân là bằng nhau.
• Đường chéo của hình thang cân bằng nhau và chia nhau làm đôi tại điểm chúng cắt nhau.

Hình thang là một hình học cơ bản nhưng linh hoạt, được ứng dụng rộng rãi trong nhiều lĩnh vực như kiến trúc, kỹ thuật và thiết kế đồ họa.

Công thức tính hình thang

Công thức tính chu vi hình thang:

C = AB + BC + CD + DA

Trong đó:

• C là chu vi hình thang
• AB, BC, CD, DA lần lượt là độ dài các cạnh của hình thang

Công thức tính diện tích hình thang:

S = (AB + CD) . \(\frac{h}{2}\)

Trong đó:

• S là diện tích hình thang
• AB, CD lần lượt là độ dài hai đáy của hình thang
• h là chiều cao của hình thang

Ngoài ra, còn có một số công thức tính đặc biệt cho các dạng hình thang riêng biệt:

• Hình thang vuông:

Diện tích: 

\(S = \frac{(AB + CD) \cdot h}{2}\) (h là độ dài cạnh góc vuông)

• Hình thang cân:

Diện tích: 

\(S = \frac{(AB + CD) \cdot h}{2}\)(h là độ dài đường trung bình)

• Hình bình hành:

Diện tích:   S=AB.h (h là độ dài đường cao)

• Hình thoi:

Diện tích: 

\(S = \frac{AC \cdot BD}{2}\) (AC và BD là hai đường chéo)

• Hình chữ nhật:

Diện tích:  S=AB.BC (AB và BC là hai cạnh kề nhau)

• Hình vuông:

Diện tích: S=\(a^2\)  (a là độ dài cạnh hình vuông)

Ví dụ:

Cho hình thang ABCD có AB // CD, AB = 5 cm, CD = 7 cm, h = 4 cm.

Chu vi hình thang ABCD là: 

C=AB+BC+CD+DA=5+BC+7+DA

Diện tích hình thang ABCD là: 

\(S = \frac{(AB + CD) \cdot h}{2} = \frac{(5 + 7) \cdot 4}{2} = 24 \, \text{cm}^2\)

Qua bài học này, chúng ta đã tìm hiểu về các tính chất của hình thang. Hiểu rõ các tính chất này sẽ giúp chúng ta giải các bài toán liên quan đến hình thang một cách dễ dàng hơn.