Hình lăng trụ đứng là một hình không gian quan trọng trong chương trình Toán lớp 8. Hình lăng trụ đứng có nhiều ứng dụng trong các lĩnh vực như xây dựng, sản xuất, vận chuyển. Bài viết này sẽ trình bày một số kiến thức cơ bản về hình lăng trụ đứng, bao gồm định nghĩa, tính chất, diện tích và thể tích.
Định nghĩa hình lăng trụ đứng
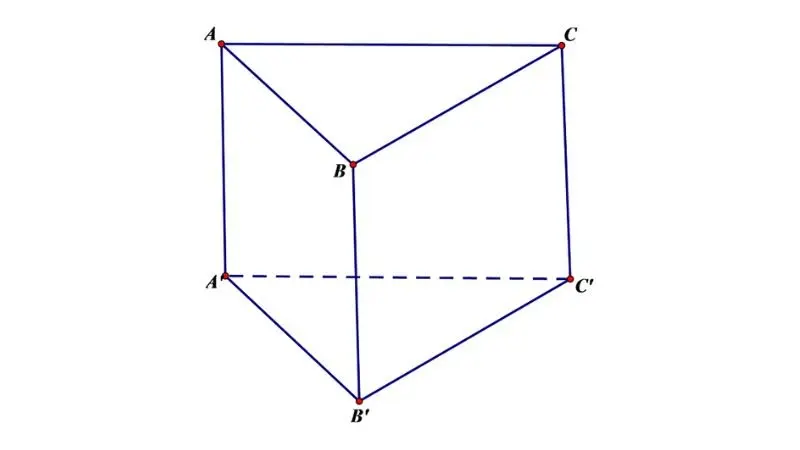
Hình lăng trụ đứng là một loại hình hộp trong không gian ba chiều. Nó được tạo thành từ một hình đáy (thường là một hình chữ nhật) và các hình chữ nhật hay hình vuông thẳng đứng (hình mặt bên) nối liền với mỗi cạnh của hình đáy và vuông góc với mặt đáy. Các cạnh của các hình mặt bên này đều có độ dài bằng nhau.
Đặc điểm chính của hình lăng trụ đứng là đối xứng quanh trục đứng của nó, có nghĩa là các hình mặt bên đều song song và cùng kích thước. Đối với một hình lăng trụ đứng có hình đáy là một hình chữ nhật, đối diện của mỗi cặp hình mặt bên là nhau và có diện tích bằng nhau.
Hình lăng trụ đứng thường được sử dụng trong nhiều lĩnh vực, bao gồm kiến trúc, công nghệ, và toán học ứng dụng. Trong kiến trúc, chúng thường được sử dụng để tạo ra các cột hoặc các phần của các tòa nhà. Trong công nghệ, chúng có thể xuất hiện dưới dạng các ống, cột hoặc các cấu trúc trụ. Trong toán học, các tính chất của hình lăng trụ đứng thường được nghiên cứu trong hình học không gian.
Các yếu tố liên quan đến hình lăng trụ đứng
Có một số yếu tố quan trọng liên quan đến hình lăng trụ đứng:
Hình đáy: Đây là hình dạng của mặt phẳng nằm dưới của hình lăng trụ đứng. Thường là một hình chữ nhật, nhưng cũng có thể là một hình vuông hoặc một hình đa giác.
Cạnh của hình đáy: Đây là các cạnh của hình đáy, xác định kích thước và hình dạng của hình lăng trụ đứng.
Chiều cao: Đây là đoạn thẳng vuông góc với mặt đáy và nối mỗi điểm trên mặt đỉnh của hình lăng trụ đứng với mặt đáy. Chiều cao này có thể khác nhau cho các hình lăng trụ khác nhau.
Các mặt bên: Các hình mặt bên của hình lăng trụ đứng là các hình chữ nhật hoặc hình vuông nằm giữa mặt đáy và mặt đỉnh và vuông góc với mặt đáy.
Mặt đỉnh: Đây là mặt phẳng nằm ở trên cùng của hình lăng trụ đứng. Thường là một hình chữ nhật có kích thước giống với hình đáy của lăng trụ.
Đường chéo: Đây là đoạn thẳng nối hai điểm trên hai mặt đỉnh của hình lăng trụ đứng không kề nhau. Đường chéo này cũng là đường cao của hình lăng trụ đứng.
Thể tích: Thể tích của hình lăng trụ đứng là khối lượng không gian mà nó chiếm. Thể tích này có thể được tính bằng cách nhân diện tích của mặt đáy với chiều cao của hình lăng trụ đứng.
Diện tích toàn phần: Diện tích toàn phần của hình lăng trụ đứng bao gồm tổng diện tích của tất cả các mặt của nó, bao gồm diện tích của mặt đáy, mặt đỉnh và các mặt bên.
Những yếu tố này đóng vai trò quan trọng trong việc tính toán và mô tả các thuộc tính của hình lăng trụ đứng trong các bài toán hình học và trong các ứng dụng thực tế.
Phân loại hình lăng trụ đứng
Hình lăng trụ đứng được phân loại dựa trên hình dạng của đáy:
Hình lăng trụ đứng tam giác:
Có hai đáy là tam giác bằng nhau và nằm trên hai mặt phẳng song song.
Các mặt bên là những hình chữ nhật.
Ví dụ: hộp bút, hộp sữa,…
Hình lăng trụ đứng tứ giác:
Có hai đáy là tứ giác bằng nhau và nằm trên hai mặt phẳng song song.
Các mặt bên là những hình chữ nhật.
Ví dụ: tủ sách, hộp đựng,…
Hình lăng trụ đứng n – giác:
Có hai đáy là n – giác bằng nhau và nằm trên hai mặt phẳng song song.
Các mặt bên là những hình chữ nhật.
Ví dụ: lăng trụ đứng ngũ giác, lăng trụ đứng lục giác,…
Ngoài ra, ta còn có thể phân loại hình lăng trụ đứng dựa trên:
Góc giữa hai cạnh bên kề nhau:
Hình lăng trụ đứng vuông: góc giữa hai cạnh bên kề nhau bằng \(90^\circ\).
Hình lăng trụ đứng xiên: góc giữa hai cạnh bên kề nhau không bằng \(90^\circ\).
Độ dài các cạnh bên:
Hình lăng trụ đứng đều: tất cả các cạnh bên bằng nhau.
Hình lăng trụ đứng không đều: một số cạnh bên có thể bằng nhau, nhưng không phải tất cả.
Lưu ý:
Hình hộp chữ nhật là một trường hợp đặc biệt của hình lăng trụ đứng tứ giác, trong đó tất cả các cạnh bằng nhau.
Hình lăng trụ đứng tam giác đều là một trường hợp đặc biệt của hình lăng trụ đứng tam giác, trong đó đáy là tam giác đều.
Tính chất
Các cạnh bên song song và bằng nhau.
Góc giữa hai cạnh bên kề nhau bằng \(90^\circ\).
Diện tích hai đáy bằng nhau.
Mặt phẳng chứa hai cạnh đáy song song với mặt phẳng chứa hai cạnh bên.
Các đường chéo của mặt đáy cắt nhau tại trung điểm mỗi đường.
Hai đường chéo AC và BD của hình lăng trụ đứng ABCD.EFGH cắt nhau tại I.
I là trung điểm của mỗi đường chéo.
AI = BI = CI = DI.
Hình lăng trụ đứng có thể chia thành ba phần:
Hai hình chóp bằng nhau.
Một hình lăng trụ có hai đáy là hai hình chóp cụt.
Diện tích xung quanh của hình lăng trụ đứng bằng chu vi đáy nhân với chiều cao.
Diện tích toàn phần của hình lăng trụ đứng bằng diện tích xung quanh cộng với diện tích hai đáy.
Thể tích của hình lăng trụ đứng bằng diện tích đáy nhân với chiều cao.
Hình lăng trụ đứng có thể được biến đổi thành hình lăng trụ đứng khác bằng cách thay đổi vị trí các mặt bên.
Hình lăng trụ đứng có thể được cắt bởi một mặt phẳng song song với hai đáy để tạo thành hai hình lăng trụ đứng khác.
Hình lăng trụ đứng có thể được cắt bởi một mặt phẳng không song song với hai đáy để tạo thành một hình chóp và một hình lăng trụ đứng khác.
Công thức tính hình lăng trụ đứng
Diện tích xung quanh: Sxq = chu vi đáy x chiều cao
Diện tích toàn phần: Stp = Sxq + 2Sđáy
Thể tích: V = Sđáy x chiều cao
Một số công thức liên quan:
Chu vi đáy n – giác: Cn = a.n
a là độ dài cạnh đáy
Diện tích tam giác:
\(S = \frac{a \times h}{2}\)a là độ dài cạnh đáy
h là chiều cao tương ứng với cạnh đáy a
Diện tích tứ giác:
\(S = \frac{a \times b \times \sin C}{2}\)a, b là độ dài hai cạnh kề nhau
C là góc giữa hai cạnh a và b
Ví dụ:
Cho hình lăng trụ đứng ABC.DEFGH có AB = 5cm, BC = 6cm, CC’ = 7cm.
Tính diện tích xung quanh: Sxq = chu vi đáy x chiều cao = (5 + 6 + 5 + 6) x 7 = 196 (cm²)
Tính diện tích toàn phần: Stp = Sxq + 2Sđáy = 196 + 2.(5.6) = 226 (cm²)
Tính thể tích: V = Sđáy x chiều cao = (5.6) x 7 = 210 (cm³)
Bài tập về hình lăng trụ đứng
Bài 1: Cho hình lăng trụ đứng ABC.DEFGH có AB = 5cm, BC = 6cm, CC’ = 7cm. Tính:
a) Diện tích xung quanh của hình lăng trụ đứng.
b) Diện tích toàn phần của hình lăng trụ đứng.
c) Thể tích của hình lăng trụ đứng.
Lời giải:
a) Diện tích xung quanh của hình lăng trụ đứng là:
Sxq = chu vi đáy x chiều cao = (AB + BC + CD + DA) x CC’ = (5 + 6 + 5 + 6) x 7 = 196 (cm²)
b) Diện tích toàn phần của hình lăng trụ đứng là:
Stp = Sxq + 2Sđáy = 196 + 2.(AB x BC) = 196 + 2.(5 x 6) = 226 (cm²)
c) Thể tích của hình lăng trụ đứng là:
V = Sđáy x chiều cao = (AB x BC) x CC’ = (5 x 6) x 7 = 210 (cm³)
Bài 2: Cho hình lăng trụ đứng tam giác ABC.A’B’C’ có đáy là tam giác vuông tại A, AB = 3cm, AC = 4cm, chiều cao AA’ = 5cm. Tính:
a) Diện tích xung quanh của hình lăng trụ đứng.
b) Diện tích toàn phần của hình lăng trụ đứng.
c) Thể tích của hình lăng trụ đứng.
Lời giải:
a) Diện tích xung quanh của hình lăng trụ đứng là:
Sxq = chu vi đáy x chiều cao = (AB + AC + BC) x AA’ = (3 + 4 + 5) x 5 = 60 (cm²)
b) Diện tích toàn phần của hình lăng trụ đứng là:
$$S_{tp} = S_{xq} + 2S_{đáy} = 60 + 2 \left( \frac{1}{2} \times AB \times AC \right) = 60 + 2 \left( \frac{1}{2} \times 3 \times 4 \right) = 72 \, \text{cm}^2$$
c) Thể tích của hình lăng trụ đứng là:
$$V = \left( \frac{1}{2} \times AB \times AC \right) \times AA’ = \left( \frac{1}{2} \times 3 \times 4 \right) \times 5 = 30 \, \text{cm}^3$$
Bài 3: Một hình lăng trụ đứng tứ giác có đáy là hình chữ nhật ABCD với AB = 4cm, BC = 6cm, chiều cao của hình lăng trụ là 8cm. Tính:
a) Diện tích xung quanh của hình lăng trụ đứng.
b) Diện tích toàn phần của hình lăng trụ đứng.
c) Thể tích của hình lăng trụ đứng.
Lời giải:
a) Diện tích xung quanh của hình lăng trụ đứng là:
Sxq = chu vi đáy x chiều cao = (AB + BC + CD + DA) x CC’ = (4 + 6 + 6 + 4) x 8 = 160 (cm²)
b) Diện tích toàn phần của hình lăng trụ đứng là:
Stp = Sxq + 2Sđáy = 160 + 2.(AB x BC) = 160 + 2.(4 x 6) = 208 (cm²)
c) Thể tích của hình lăng trụ đứng là:
V = Sđáy x chiều cao = (AB x BC) x CC’ = (4 x 6) x 8 = 192 (cm³)
Tóm lại, hình lăng trụ đứng là một hình học không gian quan trọng trong chương trình Toán lớp 8. Việc nắm vững kiến thức về hình lăng trụ đứng sẽ giúp bạn giải quyết các bài toán liên quan đến hình lăng trụ đứng một cách hiệu quả và chính xác.
