Hình hộp chữ nhật là một hình học không gian quan trọng trong chương trình Toán lớp 8. Hình hộp chữ nhật có nhiều ứng dụng trong các lĩnh vực như xây dựng, sản xuất, vận chuyển. Bài viết này sẽ trình bày một số kiến thức cơ bản về hình hộp chữ nhật, bao gồm định nghĩa, tính chất, diện tích và thể tích.
Định nghĩa hình hộp chữ nhật
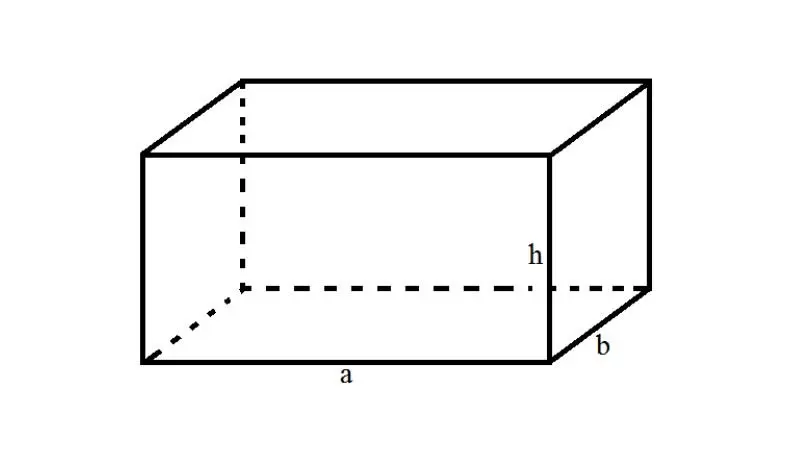
Hình hộp chữ nhật, còn được gọi là hộp chữ nhật, là một đa diện có sáu mặt, trong đó bốn mặt là hình chữ nhật và hai mặt là hình vuông. Các cạnh kề của hình chữ nhật có chiều dài bằng nhau và các góc giữa chúng là góc vuông.
Hình hộp chữ nhật có các phần tử sau:
Cạnh đáy: Đây là hình chữ nhật có độ dài và chiều rộng được xác định. Đây thường được xem là mặt dưới của hộp chữ nhật.
Chiều cao: Chiều cao của hộp chữ nhật là đoạn thẳng vuông góc với mặt đáy và nối từ mặt đỉnh của hộp chữ nhật đến mặt đáy.
Các cạnh bên: Đây là các cạnh của hình chữ nhật nằm giữa cạnh đáy và mặt đỉnh của hộp chữ nhật.
Mặt đỉnh: Đây là hình chữ nhật có kích thước giống với cạnh đáy của hộp chữ nhật và thường được xem như mặt trên của hộp chữ nhật.
Hình hộp chữ nhật là một trong những hình dạng phổ biến và quan trọng trong hình học không gian. Nó được sử dụng trong nhiều lĩnh vực, từ kiến trúc đến công nghệ và kỹ thuật.
Các yếu tố liên quan đến hình hộp chữ nhật
Có một số yếu tố quan trọng liên quan đến hình hộp chữ nhật, bao gồm:
Kích thước của các cạnh: Đây là các đoạn thẳng xác định độ dài và chiều rộng của hình chữ nhật. Kích thước này có thể ảnh hưởng đến diện tích và thể tích của hình hộp chữ nhật.
Diện tích của các mặt: Hình hộp chữ nhật có sáu mặt, bao gồm hai mặt đáy và đỉnh, cùng với bốn mặt bên. Diện tích của mỗi mặt có thể được tính để đo lường diện tích của hình hộp chữ nhật.
Thể tích: Thể tích của hình hộp chữ nhật là khối lượng không gian mà nó chiếm. Thể tích này có thể được tính bằng cách nhân diện tích của mặt đáy với chiều cao của hộp chữ nhật.
Chu vi của các cạnh: Chu vi của các cạnh của hình chữ nhật là tổng độ dài của tất cả các cạnh. Chu vi này có thể được sử dụng để tính toán chiều dài dây cần thiết để bao quanh hình hộp chữ nhật.
Đường chéo: Đường chéo của hình hộp chữ nhật là đoạn thẳng nối hai đỉnh không kề nhau của hình chữ nhật. Chiều dài của đường chéo có thể được tính bằng định lý Pythagoras.
Góc giữa các mặt: Các góc giữa các mặt của hình hộp chữ nhật là góc tạo bởi hai mặt gần nhau. Trong hình hộp chữ nhật, tất cả các góc này đều là góc vuông.
Những yếu tố này đóng vai trò quan trọng trong việc tính toán và mô tả các thuộc tính của hình hộp chữ nhật trong các bài toán hình học và trong các ứng dụng thực tế.
Tính chất của hình hộp chữ nhật
Tính chất của hình hộp chữ nhật bao gồm:
Các cạnh đối diện bằng nhau:
AB = CD, EF = GH
BC = AE, FG = HD
Các cạnh bên song song và bằng nhau:
AD // BC, EF // GH
AB // CD, EG // FH
Góc giữa hai cạnh bên kề nhau bằng \(90^\circ\):
(AB, AD) =\(90^\circ\), (BC, BF) = \(90^\circ\)
(EF, EG) = \(90^\circ\), (GH, GD) = \(90^\circ\)
Đường chéo:
Hình hộp chữ nhật có 4 đường chéo:
AC, BD, CE: là các đường chéo chính.
AF, BG, CH, DE: là các đường chéo phụ.
Tính chất:
Hai đường chéo chính cắt nhau tại trung điểm mỗi đường.
Bốn đường chéo phụ bằng nhau.
Công thức tính hình hộp chữ nhật
Diện tích:
Diện tích xung quanh:
Sxq = 2h(a + b)
Với a, b là độ dài hai cạnh đáy và h là chiều cao.
Diện tích toàn phần:
Stp = 2(ab + ah + bh)
Với a, b là độ dài hai cạnh đáy và h là chiều cao.
Thể tích:
V = abc
Với a, b, c là độ dài ba cạnh của hình hộp chữ nhật.
Chu vi đáy:
C = 2(a + b)
Với a, b là độ dài hai cạnh đáy.
Đường chéo:
$$d = \sqrt{a^2 + b^2 + c^2}$$
Với a, b, c là độ dài ba cạnh của hình hộp chữ nhật.
Ví dụ:
Cho hình hộp chữ nhật ABCD.EFGH có AB = 5cm, BC = 6cm, CC’ = 7cm.
Tính diện tích xung quanh: Sxq = 2h(a + b) = 2.7(5 + 6) = 154 (cm²)
Tính diện tích toàn phần: Stp = 2(ab + ah + bh) = 2(5.6 + 5.7 + 6.7) = 224 (cm²)
Tính thể tích: V = abc = 5.6.7 = 210 (cm³)
Bài tập về hình hộp chữ nhật
Bài 1: Một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 4cm và chiều cao 3cm. Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật đó.
Lời giải:
Diện tích xung quanh:
Sxq = 2h(a + b) = 2.3(5 + 4) = 54 (cm²)
Diện tích toàn phần:
Stp = 2(ab + ah + bh) = 2(5.4 + 5.3 + 4.3) = 110 (cm²)
Bài 2: Một hình hộp chữ nhật có thể tích 300cm³, chiều dài 15cm và chiều rộng 5cm. Tính chiều cao của hình hộp chữ nhật đó.
Lời giải:
Chiều cao của hình hộp chữ nhật là:
h = V / (ab) = 300 / (15.5) = 4 (cm)
Bài 3: Một hình hộp chữ nhật có diện tích xung quanh là 216cm² và chiều cao 6cm. Tính chu vi đáy của hình hộp chữ nhật đó.
Lời giải:
Nửa chu vi đáy của hình hộp chữ nhật là:
\(\frac{C}{2} = \frac{S_{xq}}{h} = \frac{216}{6} = 36 \, \text{cm}\)Chu vi đáy của hình hộp chữ nhật là:
\(C = 2 \times \left(\frac{C}{2}\right) = 2 \times 36 = 72 \, \text{cm}\)Bài 4: Một hình hộp chữ nhật có diện tích toàn phần là 420cm² và chiều cao 5cm. Tính diện tích một mặt đáy của hình hộp chữ nhật đó.
Lời giải:
Chu vi đáy của hình hộp chữ nhật là:
\(C = \frac{S_{tp}}{2h} = \frac{420}{2 \times 5} = 42 \, \text{cm}\)Nửa chu vi đáy của hình hộp chữ nhật là:
\(\frac{C}{2} = \frac{42}{2} = 21 \, \text{cm}\)Diện tích một mặt đáy của hình hộp chữ nhật là:
\(S = \frac{a + b}{2} = \frac{21}{2} = 10.5 \, \text{cm}^2\)Bài 5: Một hình hộp chữ nhật có chiều dài 8cm, chiều rộng 5cm và chiều cao 4cm. Một hình lập phương có cạnh bằng trung bình cộng ba kích thước của hình hộp chữ nhật. Tính diện tích toàn phần của hình lập phương đó.
Lời giải:
Trung bình cộng ba kích thước của hình hộp chữ nhật là:
\(\frac{8 + 5 + 4}{3} = 5.67 \, \text{cm}\)Cạnh của hình lập phương là:
a = 5,67 cm
Diện tích toàn phần của hình lập phương là:
\(S_{tp} = 6a^2 = 6 \times (5.67)^2 = 193.42 \, \text{cm}^2\)Tóm lại, hình hộp chữ nhật là một hình học không gian quan trọng trong chương trình Toán lớp 8. Việc nắm vững kiến thức về hình hộp chữ nhật sẽ giúp bạn giải quyết các bài toán liên quan đến hình hộp chữ nhật một cách hiệu quả và chính xác.Ngoài ra, bạn có thể tham khảo thêm các tài liệu khác để nâng cao kiến thức và kỹ năng giải bài tập về hình hộp chữ nhật.
