Trong chương trình toán học lớp 8, chúng ta đã được học về hình bình hành. Hình bình hành là một tứ giác có nhiều tính chất đặc biệt và ứng dụng rộng rãi trong thực tế.
Định nghĩa hình bình hành
Hình bình hành là một loại hình tứ giác đặc biệt trong hình học phẳng, nơi các cặp cạnh đối diện của nó không chỉ bằng nhau về độ dài mà còn song song với nhau. Cụ thể, hình bình hành có các đặc điểm và tính chất sau:
Đặc điểm:
- Các cạnh đối song song: Mỗi cạnh của hình bình hành song song với cạnh đối diện của nó.
- Các cạnh đối bằng nhau: Mỗi cạnh của hình bình hành có độ dài bằng với cạnh đối diện của nó.
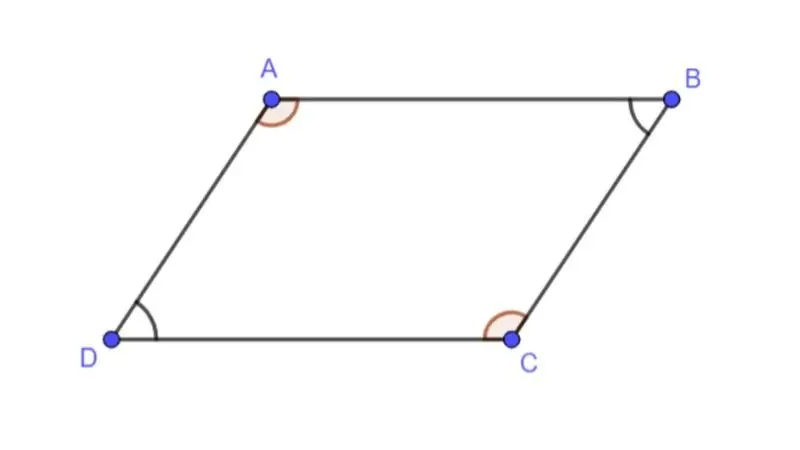
- Các góc đối bằng nhau: Các góc tạo bởi các cạnh kề của hình bình hành không nhất thiết phải là góc vuông, nhưng mỗi góc sẽ bằng với góc đối diện của nó.
Dấu hiệu nhận biết hình bình hành
Để nhận biết một hình tứ giác là hình bình hành, bạn có thể dựa vào các dấu hiệu sau đây:
Các cặp cạnh đối song song: Nếu hai cặp cạnh đối diện của tứ giác song song với nhau, tứ giác đó là hình bình hành.
Các cặp cạnh đối bằng nhau: Nếu hai cặp cạnh đối diện của tứ giác bằng nhau về độ dài, tứ giác đó là hình bình hành.
Các góc đối bằng nhau: Nếu mỗi góc của tứ giác bằng với góc đối diện của nó, tứ giác đó là hình bình hành.
Đường chéo chia nhau làm đôi tại trung điểm: Nếu một đường chéo của tứ giác chia đường chéo còn lại làm đôi tại trung điểm, tứ giác đó là hình bình hành.
Một góc và hai cạnh kề song song với hai cạnh đối: Nếu tứ giác có một góc, mà hai cạnh tạo thành góc đó song song và bằng nhau với hai cạnh đối diện, thì tứ giác đó là hình bình hành.
Các đường chéo tạo ra tam giác bằng nhau: Nếu các đường chéo của tứ giác chia nó thành hai cặp tam giác bằng nhau, tứ giác đó là hình bình hành.
Những dấu hiệu này giúp xác định một cách chính xác khi một tứ giác là hình bình hành, giúp giải quyết các bài toán hình học liên quan một cách dễ dàng hơn.
Tính chất hình bình hành
Hình bình hành là một dạng tứ giác đặc biệt với những tính chất sau:
Các cặp cạnh đối song song: Các cạnh đối diện trong hình bình hành song song với nhau.
Các cặp cạnh đối bằng nhau: Các cạnh đối diện trong hình bình hành có độ dài bằng nhau.
Các góc đối bằng nhau: Trong một hình bình hành, mỗi góc sẽ bằng với góc đối diện của nó.
Tổng hai góc kề bằng 180 độ: Tổng số đo của hai góc kề nhau trong hình bình hành là 180 độ.
Đường chéo chia nhau làm đôi: Hai đường chéo của hình bình hành cắt nhau tại trung điểm của mỗi đường, do đó chia mỗi đường chéo thành hai phần bằng nhau.
Tam giác đối xứng: Mỗi đường chéo chia hình bình hành thành hai tam giác đồng dạng và bằng nhau.
Tính chất phản chiếu: Hình bình hành có tính chất phản chiếu qua trục được tạo bởi trung điểm của hai đường chéo.
Những tính chất này giúp hình bình hành có những đặc điểm và ứng dụng độc đáo trong hình học và các bài toán liên quan.
Công thức tính hình bình hành
Diện tích:
Diện tích của hình bình hành được tính bằng công thức:
Diện tích = đáy x chiều cao
trong đó, “đáy” là độ dài của một cạnh (thường được chọn là cạnh dưới cùng), và “chiều cao” là khoảng cách vuông góc từ cạnh đáy đến cạnh đối diện.
Chu vi:
Chu vi của hình bình hành được tính bằng công thức:
Chu vi=2×(đáy + cạnh bên )
với “đáy” là độ dài của một cạnh đáy, và “cạnh bên” là độ dài của một cạnh bên.
Độ dài đường chéo:
Để tính độ dài của đường chéo, bạn có thể sử dụng định lý cosin trong trường hợp biết độ dài của hai cạnh và góc giữa chúng:
\(d^2 = a^2 + b^2 – 2ab \cos(\theta)\)trong đó d là độ dài đường chéo, a và b là độ dài của hai cạnh, và θ là góc giữa hai cạnh đó.
Góc của hình bình hành có thể được xác định thông qua việc biết một góc và sử dụng tính chất tổng hai góc kề bằng \(180^\circ\), hoặc thông qua tính chất đối xứng và song song của các cạnh.
Lưu ý rằng, trong một số trường hợp, bạn có thể cần sử dụng các phương pháp hình học bổ sung hoặc áp dụng các định lý hình học để giải quyết các bài toán phức tạp hơn liên quan đến hình bình hành.
Dạng bài tập liên quan đến hình bình hành
Ví dụ 1:
Cho tứ giác ABCD có AB // CD và AB = CD. Chứng minh rằng tứ giác ABCD là hình bình hành.
Lời giải:
- Vì AB // CD và AB = CD nên tứ giác ABCD có hai cặp cạnh đối song song và bằng nhau.
- Vậy tứ giác ABCD là hình bình hành.
Ví dụ 2:
Cho hình bình hành ABCD, biết AB = 6 cm, BC = 8 cm, chiều cao AH = 5 cm. Tính diện tích hình bình hành ABCD.
Lời giải:
- Diện tích hình bình hành ABCD bằng tích của độ dài đáy AB và chiều cao AH:
S = AB x h = 6 x 5 = 30 \(\text{cm}^2\)
Ví dụ 3:
Cho hình bình hành ABCD, M là điểm nằm trên cạnh AD. Nối BM cắt CD tại N. Chứng minh rằng MN = AM.
Lời giải:
- Xét hai tam giác AMN và BMN, ta có:
- AM = BM (vì M là trung điểm của AB)
- ∠AMN=∠BMN (vì hai góc đối của hình bình hành ABCD)
- MN là cạnh chung
- Vậy
- △AMN=△BMN (c.g.c)
- Suy ra MN = AM (hai cạnh tương ứng)
Tóm lại, hình bình hành là một tứ giác có nhiều tính chất đặc biệt và ứng dụng rộng rãi trong thực tế. Việc nắm vững các tính chất của hình bình hành sẽ giúp chúng ta giải quyết các bài toán liên quan một cách dễ dàng và hiệu quả.
