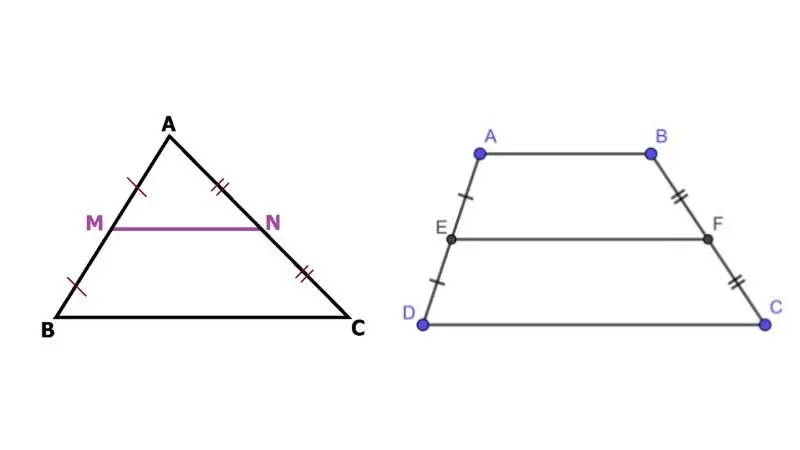
Đường trung bình của tam giác và hình thang - Toán lớp 8
Bài viết cung cấp đầy đủ kiến thức về Đường trung bình của Tam giác và Hình thang Lớp 8, bao gồm định nghĩa, tính chất, dấu hiệu nhận biết, cách vẽ hình, các dạng bài tập thường gặp và phương pháp giải chi tiết.
Đường trung bình là một khái niệm quan trọng trong môn Toán học, đặc biệt là trong các bài toán về tam giác và hình thang.Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.Bài học này sẽ giúp chúng ta tìm hiểu chi tiết hơn về đường trung bình tam giác và hình thang.
Đường trung bình của tam giác
Định nghĩa
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Ví dụ: Trong tam giác ABC, đường trung bình DE nối trung điểm D của AB và trung điểm E của AC.
Có hai cách để định nghĩa đường trung bình của tam giác:
Cách 1: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Cách 2: Cho tam giác ABC, đường thẳng đi qua trung điểm D của cạnh AB và song song với cạnh BC cắt AC tại E thì DE là đường trung bình của tam giác ABC.
Tính chất
Đường trung bình của tam giác là một đoạn thẳng nối trung điểm của hai cạnh của tam giác, và nó mang các tính chất đặc biệt sau:
Song song với cạnh thứ ba: Đường trung bình trong một tam giác luôn song song với cạnh thứ ba, tức là cạnh không được nối bởi đường trung bình.
Chiều dài bằng một nửa cạnh thứ ba: Đường trung bình của tam giác có độ dài bằng một nửa độ dài của cạnh thứ ba, cạnh mà nó song song với.
Chia tam giác thành hai phần: Đường trung bình tạo ra một tam giác nhỏ hơn trên nửa tam giác ban đầu, và tam giác nhỏ hơn này đồng dạng với tam giác ban đầu. Kết quả là, tam giác ban đầu được chia thành hai phần có diện tích bằng nhau.
Giao điểm của ba đường trung bình: Ba đường trung bình của một tam giác cắt nhau tại một điểm, được gọi là trọng tâm của tam giác. Trọng tâm này chia mỗi đường trung bình thành hai đoạn thẳng, trong đó đoạn thẳng nằm gần đỉnh của tam giác dài gấp đôi đoạn thẳng nằm gần cạnh đối diện.
Đồng dạng với tam giác gốc: Tam giác được tạo bởi ba đường trung bình trong tam giác ban đầu đồng dạng với tam giác gốc.
Các tính chất này không chỉ là cơ sở cho nhiều bài toán và chứng minh trong hình học mà còn giúp hiểu rõ hơn về cấu trúc và tỉ lệ trong các tam giác.
Chứng minh
Dạng 1: Chứng minh đường thẳng đi qua hai điểm là đường trung bình của tam giác.
Cách giải:
- Bước 1: Chứng minh hai điểm đó là trung điểm của hai cạnh của tam giác.
- Bước 2: Chứng minh đường thẳng đi qua hai điểm đó song song với cạnh thứ ba của tam giác.
Ví dụ:
Cho tam giác ABC, M và N lần lượt là trung điểm của AB và AC. Chứng minh MN // BC.
Giải:
- Ta có: M là trung điểm của AB (gt)
- N là trung điểm của AC (gt)
- => MN là đường trung bình của tam giác ABC (định nghĩa)
- => MN // BC (tính chất)
Dạng 2: Tính độ dài đường trung bình của tam giác.
Cách giải:
- Bước 1: Áp dụng tính chất đường trung bình của tam giác để tính độ dài đường trung bình.
- Bước 2: Thay các giá trị đã biết vào để tính.
Ví dụ:
Cho tam giác ABC có BC = 8cm. Tính độ dài đường trung bình MN của tam giác ABC.
Giải:
- MN // BC (tính chất)
- MN = \(\frac{1}{2}\) BC = \(\frac{1}{2}\) * 8 = 4cm (tính chất)
Dạng 3: Vận dụng tính chất đường trung bình để giải bài toán.
Cách giải:
- Bước 1: Xác định các yếu tố liên quan đến đường trung bình của tam giác.
- Bước 2: Áp dụng tính chất đường trung bình để giải bài toán.
Ví dụ:
Cho tam giác ABC có M và N lần lượt là trung điểm của AB và AC. Gọi I là trung điểm của MN. Chứng minh AI đi qua trung điểm BC.
Giải:
- MN // BC (tính chất)
- I là trung điểm của MN (gt)
- => AI // BC (tính chất)
- Gọi G là trung điểm của BC.
- Ta có: AI // BC, MN // BC
- => AI // MN
- I là trung điểm của MN (gt)
- => G là trung điểm của AI (định lí Ta-lét)
Đường trung bình của hình thang
Định nghĩa
Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
Có hai cách để định nghĩa đường trung bình của hình thang:
Cách 1: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
Cách 2: Cho hình thang ABCD, đường thẳng đi qua trung điểm E của cạnh AB và song song với hai đáy AD và BC cắt CD tại F thì EF là đường trung bình của hình thang ABCD.
Chú ý:
- Đường trung bình của hình thang không đi qua bất kỳ đỉnh nào của hình thang.
- Đường trung bình của hình thang chia hình thang thành hai hình thang con có diện tích bằng nhau.
Tính chất đường trung bình của hình thang
Đường trung bình của hình thang có hai tính chất quan trọng:
Đường trung bình song song với hai đáy của hình thang.
Chứng minh:
Xét hình thang ABCD, ta có:
-
- EF // AB // CD (tính chất đường trung bình)
- => EF // BC
Độ dài đường trung bình bằng nửa tổng độ dài hai đáy của hình thang.
Chứng minh:
Xét hình thang ABCD, ta có:
-
- EF // AB // CD (tính chất đường trung bình)
- EF = \(\frac{1}{2}\) (AB + CD) (tính chất đường trung bình)
Ngoài ra, đường trung bình của hình thang còn có một số tính chất khác như:
Đường trung bình chia hình thang thành hai hình thang con có diện tích bằng nhau.
Đường trung bình của hình thang cân đi qua trọng tâm của hình thang.
Ứng dụng: Tính chất đường trung bình của hình thang được ứng dụng để giải các bài toán liên quan đến tính diện tích, chu vi, tính độ dài các cạnh,… của hình thang.
Ví dụ:
- Cho hình thang ABCD có AB = 4cm, CD = 8cm. Tính độ dài đường trung bình MN của hình thang ABCD.
- Cho hình thang ABCD có AB = 4cm, CD = 8cm. Tính diện tích hình thang ABCD.
Hiểu rõ về tính chất đường trung bình của hình thang sẽ giúp bạn giải quyết các bài toán liên quan một cách hiệu quả và chính xác.
Chứng minh đường trung bình hình thang
Dạng 1: Chứng minh đoạn thẳng nối hai điểm là đường trung bình của hình thang.
Cách giải:
Bước 1: Chứng minh hai điểm đó là trung điểm của hai cạnh bên của hình thang.
Bước 2: Chứng minh đoạn thẳng nối hai điểm đó song song với hai đáy của hình thang.
Ví dụ:
Cho hình thang ABCD, M và N lần lượt là trung điểm của AD và BC. Chứng minh MN // AB // CD.
Giải:
- Ta có: M là trung điểm của AD (gt)
- N là trung điểm của BC (gt)
- => MN là đường trung bình của hình thang ABCD (định nghĩa)
- => MN // AB // CD (tính chất)
Dạng 2: Chứng minh tứ giác là hình thang và tính độ dài đường trung bình của hình thang.
Cách giải:
Bước 1: Chứng minh tứ giác là hình thang.
Bước 2: Áp dụng tính chất đường trung bình của hình thang để tính độ dài đường trung bình.
Ví dụ:
Cho tứ giác ABCD có AB // CD. Gọi E và F lần lượt là trung điểm của AD và BC. Chứng minh tứ giác ABEF là hình thang và tính độ dài EF.
Giải:
- Ta có: AB // CD (gt)
- E và F lần lượt là trung điểm của AD và BC (gt)
- => EF là đường trung bình của hình thang ABCD (định nghĩa)
- => EF // AB // CD (tính chất)
- => Tứ giác ABEF là hình thang (dấu hiệu nhận biết)
- EF = \(\frac{1}{2}\) (AB + CD) (tính chất)
Dạng 3: Vận dụng tính chất đường trung bình để giải bài toán.
Cách giải:
Bước 1: Xác định các yếu tố liên quan đến đường trung bình của hình thang.
Bước 2: Áp dụng tính chất đường trung bình để giải bài toán.
Ví dụ:
Cho hình thang ABCD có AB = 4cm, CD = 8cm. Gọi E và F lần lượt là trung điểm của AD và BC. Tính diện tích hình thang ABEF.
Giải:
- AB // CD (gt)
- E và F lần lượt là trung điểm của AD và BC (gt)
- => EF là đường trung bình của hình thang ABCD (định nghĩa)
- EF = \(\frac{1}{2}\) (AB + CD) = \(\frac{1}{2}\) * (4 + 8) = 6cm (tính chất)
- Diện tích hình thang ABEF = \(\frac{1}{2}\) * (EF + AB) * h = \(\frac{1}{2}\) * (6 + 4) * h (công thức tính diện tích hình thang)
Ngoài ra, bạn có thể tham khảo thêm các bài tập về chứng minh đường trung bình hình thang trong sách giáo khoa Toán lớp 8 và các sách bài tập Toán lớp 8.
Qua bài học này, chúng ta đã tìm hiểu về đường trung bình của tam giác và hình thang. Hiểu rõ về định nghĩa và tính chất của đường trung bình sẽ giúp bạn giải quyết các bài toán một cách hiệu quả và chính xác.Hy vọng bài học này đã cung cấp cho bạn những kiến thức bổ ích về đường trung bình của tam giác và hình thang.