Đối xứng tâm là một chủ đề quan trọng trong chương trình toán học lớp 8. Phép biến hình này có nhiều ứng dụng trong thực tế và giúp chúng ta giải quyết các bài toán một cách hiệu quả.
Định nghĩa đối xứng tâm
Phép đối xứng tâm là phép biến hình biến mỗi điểm M khác điểm O thành điểm M’ sao cho O là trung điểm của đoạn thẳng MM’.
Nói cách khác:
- Cho điểm O, phép biến hình biến điểm O thành chính nó, biến mỗi điểm M khác O thành M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứng tâm O.
- Điểm O được gọi là tâm đối xứng của phép biến hình.
Đặc điểm tính chất đối xứng tâm
Điểm cố định:
- Điểm O (gọi là tâm đối xứng) là điểm cố định duy nhất của phép đối xứng tâm.
- Nghĩa là: qua phép đối xứng tâm O, điểm O sẽ biến thành chính nó.
Hình ảnh của đường thẳng:
- Hình ảnh của một đường thẳng qua phép đối xứng tâm là đường thẳng song song với đường thẳng đó.
- Nghĩa là: qua phép đối xứng tâm O, đường thẳng d sẽ biến thành đường thẳng d’ song song với d.
Hình ảnh của đoạn thẳng:
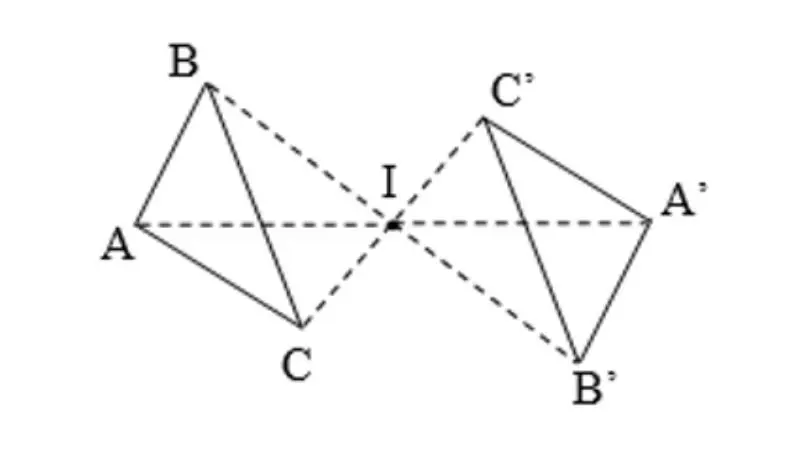
- Hình ảnh của một đoạn thẳng qua phép đối xứng tâm là đoạn thẳng bằng nó và đối xứng với nó qua tâm đối xứng.
- Nghĩa là: qua phép đối xứng tâm O, đoạn thẳng AB sẽ biến thành đoạn thẳng A’B’ bằng AB và đối xứng với AB qua O.
Hình ảnh của góc:
Hình ảnh của một góc qua phép đối xứng tâm là góc bằng nó và đối xứng với nó qua tâm đối xứng.
Nghĩa là: qua phép đối xứng tâm O, góc ∠AOB sẽ biến thành góc
∠A′OB′ bằng ∠AOB và đối xứng với ∠AOB qua O.
Hình ảnh của hình:
- Hình ảnh của một hình qua phép đối xứng tâm là hình đối xứng với hình đó qua tâm đối xứng.
- Nghĩa là: qua phép đối xứng tâm O, hình H sẽ biến thành hình H’ đối xứng với H qua O.
Ví dụ:
Hình ảnh của điểm A qua phép đối xứng tâm O là điểm A’ sao cho O là trung điểm của AA’.
Hình ảnh của đường thẳng d qua phép đối xứng tâm O là đường thẳng d’ song song với d.
Hình ảnh của đoạn thẳng AB qua phép đối xứng tâm O là đoạn thẳng A’B’ bằng AB và đối xứng với AB qua O.
Hình ảnh của góc ∠AOB qua phép đối xứng tâm O là góc ∠A′OB′ bằng ∠AOB và đối xứng với ∠AOB qua O.
Hình ảnh của hình vuông ABCD qua phép đối xứng tâm O là hình vuông A’B’C’D’ đối xứng với ABCD qua O.
Các ứng dụng của đối xứng tâm
Các ứng dụng của đối xứng tâm:
Đối xứng tâm được ứng dụng rộng rãi trong nhiều lĩnh vực như kiến trúc, nghệ thuật, khoa học kỹ thuật.
Kiến trúc: Phép đối xứng tâm được sử dụng để tạo ra các công trình có tính thẩm mỹ cao như nhà thờ, đền đài…
Ví dụ:
Nhà thờ Đức Bà Paris (Pháp): Mặt tiền nhà thờ có kiến trúc đối xứng tâm qua trục dọc.
Đền Taj Mahal (Ấn Độ): Mặt tiền đền có kiến trúc đối xứng tâm qua trục dọc.
Nghệ thuật:
Phép đối xứng tâm được sử dụng để tạo ra các tác phẩm nghệ thuật có tính cân đối và hài hòa như tranh vẽ, tượng điêu khắc…
Ví dụ:
Bức tranh “Thiếu nữ bên hoa huệ” của Leonardo da Vinci: Bức tranh có bố cục đối xứng tâm qua trục dọc.
Tượng điêu khắc “Laocoon và các con trai” của Hy Lạp: Tượng có bố cục đối xứng tâm qua trục dọc.
Khoa học kỹ thuật:
Phép đối xứng tâm được sử dụng trong các lĩnh vực như thiết kế máy móc, chế tạo dụng cụ…
Ví dụ:
Cánh quạt: Cánh quạt có thiết kế đối xứng tâm để tạo sự cân bằng khi quay.
Kính lúp: Kính lúp có thiết kế đối xứng tâm để giúp nhìn rõ các vật nhỏ.
Một số ứng dụng khác:
Phép đối xứng tâm được sử dụng trong các lĩnh vực như thời trang, đồ họa, thiết kế nội thất…
Ví dụ:
Trang phục: Nhiều trang phục có thiết kế đối xứng tâm để tạo sự thanh lịch và sang trọng.
Logo: Nhiều logo có thiết kế đối xứng tâm để tạo sự ấn tượng và dễ nhớ.
Tóm lại, đối xứng tâm là một phép biến hình quan trọng trong toán học và có nhiều ứng dụng trong thực tế. Việc nắm vững các tính chất của phép đối xứng tâm sẽ giúp chúng ta giải quyết các bài toán liên quan một cách dễ dàng và hiệu quả.
