Tổng hợp công thức diện tích xung quanh và thể tích của hình trụ
Diện tích xung quanh và thể tích của hình trụ là một chủ đề quan trọng trong chương trình Toán lớp 9. Nắm vững cách tính diện tích xung quanh và thể tích của hình trụ
Diện tích xung quanh và thể tích của hình trụ là một chủ đề quan trọng trong chương trình Toán lớp 9. Nắm vững cách tính diện tích xung quanh và thể tích của hình trụ sẽ giúp bạn giải quyết các bài toán liên quan đến hình trụ một cách hiệu quả và chính xác
Hình trụ là gì?
Là hình có hai đáy là hình tròn bằng nhau và nằm trên hai mặt phẳng song song.
Mặt phẳng đi qua trục và cắt hai đáy theo hai dây cung song song là mặt cắt trụ.
Đường sinh là đoạn thẳng vuông góc với hai đáy.
Chiều cao là khoảng cách giữa hai đáy.
Công thức diện tích xung quanh của hình trụ
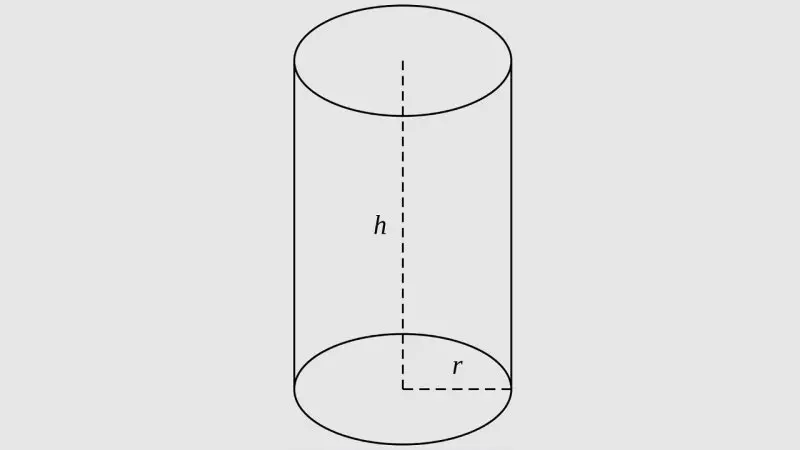
Công thức
$$Sxq = 2πRh$$
Sxq: Diện tích xung quanh của hình trụ.
π: Số Pi (π ≈ 3,14).
R: Bán kính đáy của hình trụ.
h: Chiều cao của hình trụ.
Giải thích công thức
2πRh: Chu vi đáy hình trụ * Chiều cao hình trụ.
Thể tích xung quanh của hình trụ
Định nghĩa
Thể tích của hình trụ là thể tích của phần không gian được giới hạn bởi mặt xung quanh và hai đáy của hình trụ.
Công thức
$$V = πR²h$$
V: Thể tích của hình trụ.
π: Số Pi (π ≈ 3,14).
R: Bán kính đáy của hình trụ.
h: Chiều cao của hình trụ.
Giải thích công thức
πR²: Diện tích đáy hình trụ * Chiều cao hình trụ.
Các dạng toán thường gặp
Dạng 1: Tính diện tích xung quanh, thể tích của hình trụ khi biết bán kính đáy và chiều cao.
Ví dụ:
Cho hình trụ có bán kính đáy R = 5cm, chiều cao h = 10cm.
a) Tính diện tích xung quanh của hình trụ.
b) Tính thể tích của hình trụ.
Lời giải:
a) Diện tích xung quanh của hình trụ là:
Sxq = 2πRh = 2 x 3,14 x 5 x 10 = 314cm²
b) Thể tích của hình trụ là:
V = πR²h = 3,14 x 5² x 10 = 785cm³
Dạng 2: Tính bán kính đáy, chiều cao khi biết diện tích xung quanh, thể tích và một trong hai đại lượng kia.
Ví dụ:
Một hình trụ có diện tích xung quanh là 94,2cm², chiều cao h = 5cm. Tính bán kính đáy của hình trụ.
Một hình trụ có thể tích là 1570cm³, chiều cao h = 10cm. Tính bán kính đáy của hình trụ.
Lời giải:
Bán kính đáy của hình trụ là:
\(R = \frac{S \times q}{2\pi h} = \frac{94.2 \, \text{cm}^2}{2 \times 3.14 \times 5 \, \text{cm}} = 3 \, \text{cm}\)
Bán kính đáy của hình trụ là:
\(R = \sqrt{\frac{V}{\pi h}} = \sqrt{\frac{1570 \, \text{cm}^3}{3.14 \times 10 \, \text{cm}}} = 6 \, \text{cm}\)
Dạng 3: Vận dụng tính diện tích xung quanh, thể tích vào giải bài toán thực tế.
Ví dụ:
Một cái thùng phuy hình trụ có bán kính đáy R = 30cm, chiều cao h = 60cm. Người ta đổ đầy nước vào thùng. Hỏi thùng chứa được bao nhiêu lít nước?
Lời giải:
Thể tích nước thùng chứa được là:
V = πR²h = 3,14 x 30² x 60 = 169560cm³ = 169,56 lít
Giải bài tập sách giáo khoa Toán lớp 9 – Diện tích xung quanh và thể tích của hình trụ
Bài 40:
Một hình chóp tứ giác đều có độ dài cạnh bên bằng 25cm, đáy là hình vuông cạnh 4cm.
a) Tính diện tích xung quanh của hình chóp.
b) Tính diện tích toàn phần của hình chóp.
Lời giải:
a) Diện tích xung quanh của hình chóp là:
Sxq = p x d = 4 x 25 = 100cm²
b) Diện tích đáy của hình chóp là:
Sđáy = a² = 4² = 16cm²
Diện tích toàn phần của hình chóp là:
S = Sxq + Sđáy = 100cm² + 16cm² = 116cm²
Bài 41:
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, trung đoạn SO = h.
a) Chứng minh rằng SO vuông góc với mặt phẳng (ABCD).
b) Tính diện tích xung quanh của hình chóp theo a và h.
Lời giải:
a) Ta có:
SO là trung đoạn của hình chóp tứ giác đều.
Mặt phẳng (ABCD) là mặt phẳng đáy.
Vì vậy, SO vuông góc với mặt phẳng (ABCD).
b) Diện tích xung quanh của hình chóp là:
Sxq = p x d = 4 x a/2 x h = 2ah
Bài 42:
Tính độ dài đường cao của hình chóp tứ giác đều với các kích thước cho trên hình vẽ:
[Hình vẽ]
Lời giải:
Gọi O là trung điểm của AB.
Ta có:
SO là trung đoạn của hình chóp tứ giác đều.
SO vuông góc với mặt phẳng (ABCD).
SA là cạnh bên của hình chóp.
AO là đường trung tuyến của tam giác SAC vuông tại A.
Áp dụng định lí Py-ta-go vào tam giác vuông SAC, ta có:
SA² = SC² – AC² = 10² – 4² = 84
Áp dụng định lí Py-ta-go vào tam giác vuông SAO, ta có:
SO² = SA² – AO² = 84 – 2² = 80
Suy ra SO = √80 = 4√5cm.
Vậy độ dài đường cao của hình chóp là 4√5cm.
Bài 43:
Tính diện tích xung quanh, diện tích toàn phần của các hình chóp tứ giác đều sau đây:
a) Hình chóp có độ dài cạnh bên là 5cm, cạnh đáy là 4cm.
b) Hình chóp có độ dài đường cao là 6cm, cạnh đáy là 4cm.
Lời giải:
a) Diện tích xung quanh của hình chóp là:
Sxq = p x d = 4 x 5 = 20cm²
Diện tích đáy của hình chóp là:
Sđáy = a² = 4² = 16cm²
Diện tích toàn phần của hình chóp là:
S = Sxq + Sđáy = 20cm² + 16cm² = 36cm²
b) Diện tích xung quanh của hình chóp là:
Sxq = p x d = 4 x 6/2 x 4 = 24cm²
Diện tích đáy của hình chóp là:
Sđáy = a² = 4² = 16cm²
Diện tích toàn phần của hình chóp là:
S = Sxq + Sđáy = 24cm² + 16cm² = 40cm²
Bài viết đã cung cấp cho bạn đầy đủ kiến thức về diện tích xung quanh và thể tích của hình trụ. Hy vọng những thông tin này hữu ích cho bạn và giúp bạn giải quyết tốt các bài toán liên quan đến diện tích xung quanh và thể tích của hình trụ.
Chúc bạn học tốt với toanhoc.edu.vn
Bài Viết Liên Quan
Với niềm đam mê mãnh liệt đối với toán học, tôi luôn mong muốn truyền tải kiến thức và khơi gợi niềm yêu thích môn học này cho thế hệ trẻ. Tôi luôn tận tâm trong công việc giảng dạy, sử dụng phương pháp giảng dạy sáng tạo và hiệu quả để giúp học sinh tiếp thu kiến thức một cách dễ dàng và hứng thú. Với những thành tựu xuất sắc trong lĩnh vực toán học, tôi đã nhận được nhiều giải thưởng danh giá và được cộng đồng khoa học đánh giá cao. Tôi là nguồn cảm hứng và tấm gương sáng cho các thế hệ học sinh và sinh viên yêu thích toán học.









