Kỳ thi tuyển sinh lớp 10 là một sự kiện quan trọng trong cuộc đời mỗi học sinh. Bài viết này sẽ trình bày hướng dẫn giải chi tiết đề thi tuyển sinh lớp 10 môn toán 2023-2024, giúp các em ôn tập và củng cố kiến thức, đồng thời rút ra kinh nghiệm cho kỳ thi sắp tới của mình.
Đề thi tuyển sinh lớp 10 THPT năm học 2023-2024 Hà Nội
Giải chi tiết
Câu I
1) Tính giá trị của biểu thức A khi \(x=9\).
Thay \(x=9\) vào biểu thức A, ta được:
\begin{align*}
A &= \frac{9 + 2}{\sqrt{9}} \\
&= \frac{11}{3}
\end{align*}
2)
\begin{align*}
B &= \frac{2\sqrt{x}-3}{\sqrt{x}-1} + \frac{3-\sqrt{x}}{x-1} \\
&= \frac{2\sqrt{x}-3}{\sqrt{x}-1} + \frac{3-\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)} \\
&= \frac{2\sqrt{x}(\sqrt{x}+1)-3(\sqrt{x}+1)+3-\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)} \\
&= \frac{2x+2\sqrt{x}-3\sqrt{x}-3+3-\sqrt{x}}{x-1} \\
&= \frac{2x-\sqrt{x}}{x-1} \\
&= \frac{\sqrt{x}(2\sqrt{x}-1)}{\sqrt{x}(\sqrt{x}+1)} \\
&= \frac{2\sqrt{x}-1}{\sqrt{x}+1}
\end{align*}
3) Tìm tất cả giá trị của x để A.B = 4.
\begin{align*}
A.B &= 4 \\
\Rightarrow \frac{x+2}{\sqrt{x}} \cdot \frac{2\sqrt{x}}{\sqrt{x}+1} &= 4 \\
\Rightarrow \frac{2(x+2)}{\sqrt{x}+1} &= 4 \\
\Rightarrow x+2 &= 2(\sqrt{x}+1) \\
\Rightarrow x+2 &= 2\sqrt{x}+2 \\
\Rightarrow x &= 2\sqrt{x} \\
\Rightarrow x^2 &= 4x \\
\Rightarrow x(x-4) &= 0 \\
\Rightarrow x=0 \text{ hoặc } x=4
\end{align*}
Tuy nhiên, x>0 nên x=4 là nghiệm duy nhất.
Vậy x=4.
Câu II
1) Gọi số sản phẩm mà phân xưởng phải làm mỗi ngày theo kế hoạch là \( x \) (sản phẩm).
Theo đề bài, ta có hệ phương trình:
\begin{align*}
3x &= 900 \\
(x + 15)(3 – 1) &= 900 – 3x
\end{align*}
Giải hệ phương trình, ta được:
\begin{align*}
x &= 300 \\
x + 15 &= 100
\end{align*}
Vậy theo kế hoạch, mỗi ngày phân xưởng phải làm 300 sản phẩm.
2) Thể tích của khối gỗ dạng hình trụ được tính theo công thức \( V = \pi r^2 h \).
\[
V = \pi r^2 h = 3.14 \cdot 30^2 \cdot 120 = 339120 \text{ cm}^3
\]
Vậy thể tích của khối gỗ là 339120 cm\(^3\).
\(V = \pi r^2 h = 3.14 \cdot 30^2 \cdot 120 = 339120 \text{ cm}^3\)
Vậy thể tích của khối gỗ là 339120 cm\(^3\).
Câu III (2,5 điểm)
1) Gọi số sản phẩm mà phân xưởng phải làm mỗi ngày theo kế hoạch là \( x \) (sản phẩm).
Theo đề bài, ta có hệ phương trình:
\begin{align*}
3x &= 900 \\
(x + 15)(3 – 1) &= 900 – 3x
\end{align*}
Giải hệ phương trình, ta được:
\begin{align*}
x &= 300 \\
x + 15 &= 315
\end{align*}
Vậy theo kế hoạch, mỗi ngày phân xưởng phải làm 300 sản phẩm.
2) Thể tích của khối gỗ dạng hình trụ được tính theo công thức \( V = \pi r^2 h \).
\[
V = \pi r^2 h = 3.14 \cdot 30^2 \cdot 120 = 339120 \text{ cm}^3
\]
Vậy thể tích của khối gỗ là 339120 cm\(^3\).
Câu IV
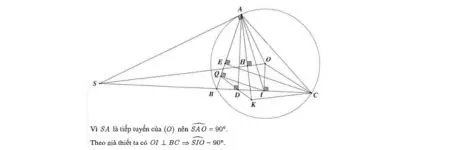
Xét tứ giác \(SAOI\) có \(\angle SAO + \angle SIO = 180^\circ\), mà hai góc \(SAO\) và \(SIO\) là hai góc đối nhau nên tứ giác \(SAOI\) là tứ giác nội tiếp.
Ta có \(\triangle OAH\) vuông tại \(H\) nên \(\angle OAH = 90^\circ – \angle HOA\).
Ta có \(\triangle IAD\) vuông tại \(D\) nên \(\angle IAD = 90^\circ – \angle DIA\).
Vì \(\angle HOA = \angle DIA\) (hai góc nội tiếp cùng chắn cung \(SA\) của đường tròn ngoại tiếp tứ giác \(SAOI\) nên \(\angle OAH = \angle IAD\).
Ta có \(QI\), \(QI\) làn lượt là trung đẳng các đoạn thẳng \(BE\), \(BC\) \(\Rightarrow QI\) là đường trung bình của \(\triangle BEC\) \(\Rightarrow QI \parallel EC\).
Vì \(EC \perp AB\) và \(QI \parallel EC\) nên \(QI \perp AB\), do đó \(\angle BQI = 90^\circ\).
Xét \(\triangle BDA\) và \(\triangle BQA\) cùng có chung \(ABC\), mà khác \(BDA = BQI = 90^\circ\).
Suy ra \(\triangle BDA \cong \triangle BQA\) (g.c.g).
\(\Rightarrow \frac{BA}{BI} = \frac{BD}{BQ} \Rightarrow BA \cdot BQ = BD \cdot BI\).
Ta có \(\angle AQI = \angle ADI = 90^\circ\) nên tứ giác \(AQDI\) là tứ giác nội tiếp.
Suy ra \(\angle KDC = \angle BAI\). (1)
Xét \(\triangle BAD\) vuông tại \(D\) có \(\angle BAD = 90^\circ – \angle ABC\). (2a)
Xét \(\triangle OAC\) có \(OA = OC = R\)). Suy ra \(\triangle OAC\) cân tại đỉnh \(O\).
Suy ra \(\angle OAC = 90^\circ – \frac{1}{2} \angle AOC\). (2b)
Trong đường tròn (O), ta có \(\angle ABC = \frac{1}{2} \angle AOC\) (tính chất góc nội tiếp và góc ở tâm cùng chắn cung \(AC\)).
Từ (2a), (2b) và (2c) suy ra \(\angle BAD = \angle OAC\).
Theo chứng minh ý 2, có \(\angle IAD = \angle OAH\).
Suy ra \(\angle BAD + \angle IAD = \angle OAC + \angle OAH \Rightarrow \angle BAI = \angle KAC\). (2)
Từ (1) và (2) suy ra \(\angle KDC = \angle KAC\).
Xét tứ giác \(ADKC\) có \(\angle KDC = \angle KAC\), mà hai đỉnh \(A\), \(D\) kề nhau, suy ra tứ giác \(ADKC\) là tứ giác nội tiếp.
Suy ra \(\angle AKC = \angle ADC \Rightarrow \angle AKC = 90^\circ \Rightarrow CK \perp AH\).
Ta có \(SO \parallel AH\) và \(CK \perp AH\) nên \(CK \parallel SO\).
Câu V:
Do \( a > 0 \), \( b > 0 \) nên bất đẳng thức được chứng minh tương đương với
\[ a^2(a^2 + b^2) + ab(a + b) + b^2(a^2 + b^2) \geq 4ab(a + b) \]
\[ \Leftrightarrow a^4 + b^4 + a^3b + ab^3 + 5a^2b^2 + b^4 + a^4 + ab \geq 4ab + 4ab(a + b) \]
\[ \Leftrightarrow a^4 + 5a^2b^2 + a^3b + ab^3 + 5a^2b^2 + b^4 + a^4 + ab \geq 4ab(a + b + 1) \]
\[ \Leftrightarrow a^4 + 5a^2b^2 + a^3b + ab^3 + 5a^2b^2 + b^4 + a^4 + ab \geq 4ab(a + b + 1) \quad (\text{vì } a > 0). \]
Do \( a > 0 \), \( b > 0 \) và \( a + b \geq 2\sqrt{ab} \) nên \( a + b + 1 \geq 2\sqrt{ab} + 1. \)
Suy ra \( 4ab(a + b + 1) \geq 4ab(2\sqrt{ab} + 1) \) (đpcm).
Chúc các bạn ôn tập hiệu quả và đạt kết quả cao trong kỳ thi THPT quốc gia !
