Chu vi hình chữ nhật là một khái niệm quan trọng trong chương trình Toán lớp 3. Hiểu rõ về chu vi hình chữ nhật sẽ giúp học sinh giải quyết được nhiều bài toán liên quan đến hình chữ nhật và các hình khác.
Chu vi hình chữ nhật là gì?
Chu vi hình chữ nhật là tổng độ dài của bốn cạnh của hình chữ nhật.
Công thức tính chu vi hình chữ nhật
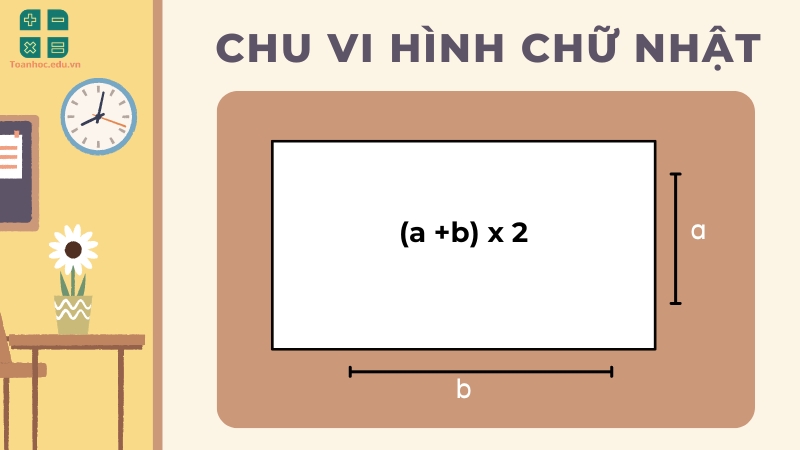
Công thức chu vi hình chữ nhật
$$P = (a + b) x 2$$
trong đó:
P là chu vi hình chữ nhật
a là chiều dài hình chữ nhật
b là chiều rộng hình chữ nhật
Ví dụ:
Một hình chữ nhật có chiều dài 5cm, chiều rộng 3cm. Chu vi hình chữ nhật là:
P = (5 + 3) x 2 = 16 (cm)
Đơn vị đo chu vi
Đơn vị đo chu vi thường dùng là:
Xăng-ti-mét (cm)
Mét (m)
Ki-lô-mét (km)
Cách tính nửa chu vi hình chữ nhật
Nửa chu vi hình chữ nhật bằng tổng chiều dài và chiều rộng, bằng 1/2 chu vi hình chữ nhật.
Công thức: C = \(\frac{P}{2}\) = a + b
Trong đó:
C là nửa chu vi hình chữ nhật (đơn vị độ dài m, cm, mm,…)
P là chu vi hình chữ nhật (đơn vị độ dài m, cm, mm,…)
a là chiều dài hình chữ nhật (đơn vị độ dài m, cm, mm,…)
b là chiều rộng hình chữ nhật (đơn vị độ dài m, cm, mm,…)
Một số dạng bài tập tính chu vi hình chữ nhật:
Dạng 1: Tính chu vi hình chữ nhật khi biết chiều dài và chiều rộng.
Ví dụ:
Một hình chữ nhật có chiều dài 5cm, chiều rộng 3cm. Chu vi hình chữ nhật đó là:
P = (5 + 3) x 2 = 16 (cm)
Dạng 2: Tìm chiều dài hoặc chiều rộng khi biết chu vi và một cạnh của hình chữ nhật.
Ví dụ:
Một hình chữ nhật có chu vi là 32cm và chiều rộng là 8cm. Tính chiều dài của hình chữ nhật đó.
Giải:
Chiều dài hình chữ nhật = \(\frac{Chu vi – 2 x chiều rộng} {2}\)
Chiều dài hình chữ nhật = (32 – 2 x 8) / 2 = 8 (cm)
Dạng 3: So sánh chu vi hai hình chữ nhật.
Ví dụ:
So sánh chu vi hai hình chữ nhật có chiều dài lần lượt là 4cm và 6cm, chiều rộng lần lượt là 3cm và 5cm.
Giải:
Chu vi hình chữ nhật 1 = (4 + 3) x 2 = 14 (cm)
Chu vi hình chữ nhật 2 = (6 + 5) x 2 = 22 (cm)
Chu vi hình chữ nhật 2 > Chu vi hình chữ nhật 1 (22 cm > 14 cm)
Dạng 4: Vẽ hình chữ nhật theo chu vi cho trước.
Ví dụ:
Vẽ hình chữ nhật có chu vi là 28cm và chiều rộng là 5cm.
Giải:
Nửa chu vi hình chữ nhật = \(\frac{Chu vi} {2} = \frac{28}{2} = 14\) (cm)
Chiều dài hình chữ nhật = Nửa chu vi – Chiều rộng = 14 – 5 = 9 (cm)
Vẽ hình chữ nhật có chiều dài 9cm, chiều rộng 5cm.
Bài tập sách giáo khoa
Bài 1:
a) Vẽ hình chữ nhật ABCD có chiều dài 6cm, chiều rộng 4cm.
b) Nối hai đỉnh đối diện A và C, B và D.
c) Em nhận xét gì về hai hình tam giác ABC và ADC?
d) Chu vi hình chữ nhật ABCD bằng bao nhiêu xăng-ti-mét?
Bài 2:
Một mảnh bìa hình chữ nhật có chiều dài 8cm, chiều rộng 5cm. Chu vi mảnh bìa hình chữ nhật bằng bao nhiêu xăng-ti-mét?
Bài 3:
Ghép bốn tấm bìa hình vuông cạnh 2cm thành một hình chữ nhật. Tính chu vi hình chữ nhật đó.
Bài 4:
Vẽ hình chữ nhật ABCD có chiều dài 6cm, chiều rộng 4cm. Vẽ hai đường chéo AC và BD cắt nhau tại E. So sánh chu vi hình chữ nhật ABCD với chu vi tam giác ABE.
Gợi ý giải bài tập
Bài 1:
a) Vẽ hình chữ nhật ABCD có chiều dài 6cm, chiều rộng 4cm.
b) Nối hai đỉnh đối diện A và C, B và D.
c) Hai hình tam giác ABC và ADC bằng nhau.
d) Chu vi hình chữ nhật ABCD = (chiều dài + chiều rộng) x 2 = (6 + 4) x 2 = 20 (cm).
Bài 2:
Chu vi mảnh bìa hình chữ nhật = (chiều dài + chiều rộng) x 2 = (8 + 5) x 2 = 26 (cm).
Bài 3:
Chu vi hình chữ nhật = (chiều dài + chiều rộng) x 2 = (4 x 2 + 2 x 2) x 2 = 16 (cm).
Bài 4:
Chu vi hình chữ nhật ABCD = (chiều dài + chiều rộng) x 2 = (6 + 4) x 2 = 20 (cm).
Chu vi tam giác ABE = \(\frac{1}{2}\) x cạnh x 4 = \(\frac{1}{2}\) x 6 x 4 = 12 (cm).
Chu vi hình chữ nhật ABCD > chu vi tam giác ABE (20 cm > 12 cm).
Chu vi hình chữ nhật là một kiến thức toán học cơ bản mà học sinh lớp 3 cần nắm vững. Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích về chu vi hình chữ nhật.








