Trong hình học, việc nghiên cứu về vị trí tương đối của hai đường tròn là một chủ đề quan trọng và hấp dẫn. Khi hai đường tròn tương tác với nhau, chúng có thể có nhiều vị trí tương đối khác nhau, từ việc không giao nhau cho đến việc đồng tâm.
Sự hiểu biết về các vị trí này không chỉ mở ra cánh cửa cho sự khám phá trong lĩnh vực hình học mà còn cung cấp cơ sở cho việc giải quyết nhiều bài toán thực tế. Hãy cùng khám phá chi tiết về vị trí tương đối của hai đường tròn trong bài viết dưới đây.
Định nghĩa chung vị trí tương đối của hai đường tròn
Vị trí tương đối của hai đường tròn là cách mà chúng tương tác và đặt vị trí đối với nhau trong mặt phẳng hoặc không gian ba chiều. Có nhiều trường hợp khác nhau mà hai đường tròn có thể xuất hiện, từ việc không giao nhau cho đến việc đồng tâm.
Hai đường tròn không giao nhau
Hai đường tròn không giao nhau là hai đường tròn không có điểm chung nào. Tức là, không có điểm nào trong mặt phẳng mà khoảng cách từ điểm đó đến hai tâm của hai đường tròn đều lớn hơn tổng của hai bán kính.
Điều này có thể diễn ra trong các trường hợp sau:
Đường tròn nằm ngoài: Một đường tròn nằm hoàn toàn bên ngoài đường tròn kia và cả hai có bán kính khác nhau và không có điểm chung.
Đường tròn nằm trong: Một đường tròn nằm hoàn toàn bên trong đường tròn kia và cả hai có bán kính khác nhau và không có điểm chung.
Đường tròn đồng tâm: Hai đường tròn có cùng tâm, nhưng có bán kính khác nhau. Trong trường hợp này, không có điểm nào nằm trong vùng giao của hai đường tròn.
Trong tất cả các trường hợp này, vị trí tương đối của hai đường tròn không giao nhau, và điều này có thể được xác định bằng cách so sánh khoảng cách giữa hai tâm với tổng của hai bán kính.
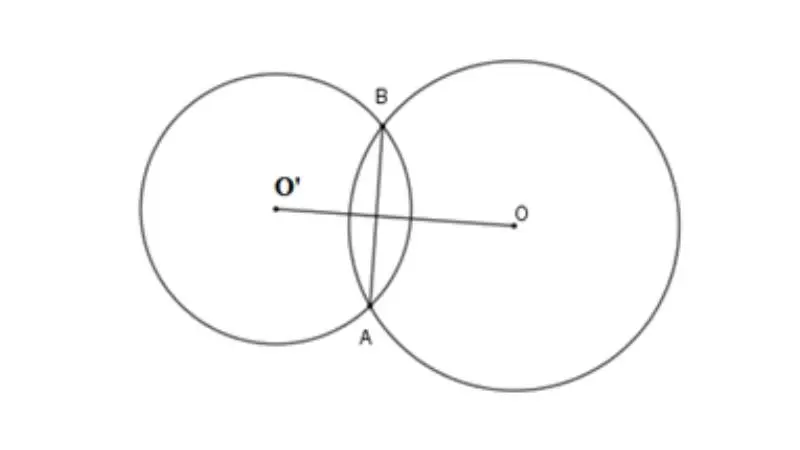
Hai đường tròn giao nhau
Hai đường tròn giao nhau khi có ít nhất một điểm nằm trên cả hai đường tròn. Tức là, tồn tại ít nhất một điểm thuộc cả hai đường tròn đồng thời.
Trong trường hợp hai đường tròn giao nhau, có một số điểm cần xem xét:
Số điểm giao nhau: Số điểm giao nhau của hai đường tròn có thể là một, hai hoặc nhiều hơn tùy thuộc vào vị trí tương đối của chúng.
Tọa độ các điểm giao nhau: Điểm hoặc các điểm giao nhau của hai đường tròn có thể có tọa độ được xác định thông qua giải hệ phương trình của hai đường tròn.
Tính chất hình học: Khi hai đường tròn giao nhau, chúng tạo ra các điểm chung và tạo thành một vùng giao của chúng trong mặt phẳng. Các tính chất hình học của vùng giao này có thể được nghiên cứu để giải quyết các bài toán liên quan.
Tóm lại, khi hai đường tròn giao nhau, điều quan trọng là xác định số lượng và tọa độ của các điểm giao nhau cũng như nghiên cứu các tính chất hình học của vùng giao của chúng.
Hai đường tròn tiếp xúc ngoài
Hai đường tròn tiếp xúc ngoài khi chúng chỉ chạm nhau tại một điểm duy nhất, và không có điểm nào thuộc cả hai đường tròn. Điểm tiếp xúc này là điểm duy nhất mà khoảng cách từ tâm của mỗi đường tròn đến điểm đó bằng tổng của hai bán kính.
Trong trường hợp hai đường tròn tiếp xúc ngoài, một số điều quan trọng cần lưu ý:
Số điểm tiếp xúc: Chỉ có một điểm tiếp xúc ngoài duy nhất giữa hai đường tròn.
Tọa độ của điểm tiếp xúc: Tọa độ của điểm tiếp xúc ngoài có thể được xác định bằng cách giải hệ phương trình của hai đường tròn.
Tính chất hình học: Khi hai đường tròn tiếp xúc ngoài, chúng tạo ra một đường chung qua điểm tiếp xúc, làm cho đường này là một đường tiếp tuyến chung của cả hai đường tròn.
Khoảng cách giữa tâm: Khoảng cách giữa tâm của hai đường tròn là tổng của hai bán kính. Điều này làm cho hai đường tròn không cắt nhau và chỉ tiếp xúc tại điểm tiếp xúc duy nhất.
Hai đường tròn tiếp xúc trong
Hai đường tròn tiếp xúc trong khi chúng chỉ chạm nhau tại một điểm duy nhất, và một trong hai đường tròn nằm hoàn toàn bên trong đường tròn kia. Điểm tiếp xúc này là điểm duy nhất mà khoảng cách từ tâm của đường tròn lớn hơn bán kính của đường tròn kia trừ đi bán kính của chính nó.
Trong trường hợp hai đường tròn tiếp xúc trong, một số điều quan trọng cần lưu ý:
Số điểm tiếp xúc: Chỉ có một điểm tiếp xúc trong duy nhất giữa hai đường tròn.
Tọa độ của điểm tiếp xúc: Tọa độ của điểm tiếp xúc trong có thể được xác định bằng cách giải hệ phương trình của hai đường tròn.
Tính chất hình học: Khi hai đường tròn tiếp xúc trong, đường tròn nằm bên trong sẽ là một phần của đường tròn lớn hơn. Điểm tiếp xúc nằm trong vùng bên trong đường tròn lớn hơn.
Khoảng cách giữa tâm: Khoảng cách giữa tâm của hai đường tròn là hiệu của bán kính của đường tròn lớn trừ đi bán kính của đường tròn nhỏ.
Tóm lại, khi hai đường tròn tiếp xúc trong, điều quan trọng là xác định vị trí của điểm tiếp xúc và các tính chất hình học của vùng bên trong đường tròn lớn hơn.
Nhìn chung việc nghiên cứu về vị trí tương đối của hai đường tròn không chỉ là một chủ đề hấp dẫn trong hình học mà còn mang lại những ứng dụng quan trọng trong thực tế. Hiểu biết sâu hơn về các vị trí này giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các đường tròn và làm cho việc giải quyết các bài toán hình học trở nên dễ dàng hơn. Đồng thời, sự hiểu biết này cũng mở ra cánh cửa cho nhiều hướng nghiên cứu mới trong tương lai.
