Lý thuyết về cung chứa góc - Toán lớp 9

Cung chứa góc là một phần của đường tròn được giới hạn bởi hai điểm A và B trên đường tròn, trong đó hai điểm A và B tạo thành một góc. Hiểu rõ về cung chứa góc giúp học sinh giải quyết nhiều dạng toán liên quan đến đường tròn như tính độ dài cung, diện tích hình quạt, …

Định nghĩa cung chứa góc

Cung chứa góc là phần của đường tròn giới hạn bởi hai điểm A và B trên đường tròn, trong đó hai điểm A và B tạo thành một góc.

Có hai cách định nghĩa cung chứa góc:

Cách 1:

Cho đường tròn (O) và hai điểm A, B trên đường tròn.

Góc \(\angle AOB\) là góc nội tiếp chắn cung \(\stackrel{\frown}{AB}\).

Cung chứa \(\angle AOB\) là phần của đường tròn giới hạn bởi hai điểm A và B, bao gồm cả hai điểm A và B.

Cách 2:

Cho đường tròn (O) và hai điểm A, B trên đường tròn.

Nối A và B, ta được đoạn thẳng AB.

Cung chứa \(\angle AOB\) là tập hợp tất cả các điểm M trên đường tròn nằm cùng phía với AB so với điểm O.

Cung chứa góc có thể là cung nhỏ hoặc cung lớn:

Cung nhỏ: Cung nhỏ hơn nửa đường tròn.

Cung lớn: Cung lớn hơn nửa đường tròn.

Ví dụ:

• Cho đường tròn (O) và hai điểm A, B trên đường tròn sao cho \(\angle AOB\) = \(60^\circ\).
• Cung AmB là cung chứa góc \(\angle AOB\).
• Cung AmB có thể là cung nhỏ hoặc cung lớn.

Phân loại cung chứa góc

Cung chứa góc được phân loại dựa trên số đo của nó:

Cung nhỏ:

Định nghĩa: Cung nhỏ là cung có số đo nhỏ hơn 180°.

Đặc điểm:

• • Cung nhỏ luôn nằm bên trong đường tròn.
  • Cung nhỏ không bao gồm hai điểm A và B.

Cung lớn:

Định nghĩa: Cung lớn là cung có số đo lớn hơn hoặc bằng \(180^\circ\) và nhỏ hơn \(360^\circ\).

Đặc điểm:

Cung lớn có thể nằm bên trong hoặc bên ngoài đường tròn.

Cung lớn bao gồm cả hai điểm A và B.

Cung nửa đường tròn:

Định nghĩa: Cung nửa đường tròn là cung có số đo bằng 180°.

Đặc điểm:

• • Cung nửa đường tròn luôn nằm bên trong đường tròn.
  • Cung nửa đường tròn bao gồm cả hai điểm A và B.

Ví dụ:

Cho đường tròn (O) và hai điểm A, B trên đường tròn sao cho \(\angle AOB\) = 120°.

Cung AmB là cung chứa góc \(\angle AOB\).

Cung AmB là cung nhỏ vì sđ \(\stackrel{\frown}{AmB}\)= 120° < 180°.

Cho đường tròn (O) và hai điểm A, B trên đường tròn sao cho \(\angle AOB\) = 240°.

Cung AmB là cung chứa góc \(\angle AOB\).

Cung AmB là cung lớn vì sđ \(\stackrel{\frown}{AmB}\) = 240° > 180°.

Tính chất về cung chứa góc

Hai cung chứa góc bằng nhau: Hai cung chứa góc bằng nhau nếu hai cung này có cùng số đo.

Ví dụ:

Cho đường tròn (O) và hai điểm A, B trên đường tròn.

Cung \(\stackrel{\frown}{AmB}\) và cung \(\stackrel{\frown}{AnB}\) có số đo bằng nhau ( sđ \(\stackrel{\frown}{AmB}\) = sđ  \(\stackrel{\frown}{AnB}\) ).

Do đó, \(\stackrel{\frown}{AmB}\) = \(\stackrel{\frown}{AnB}\).

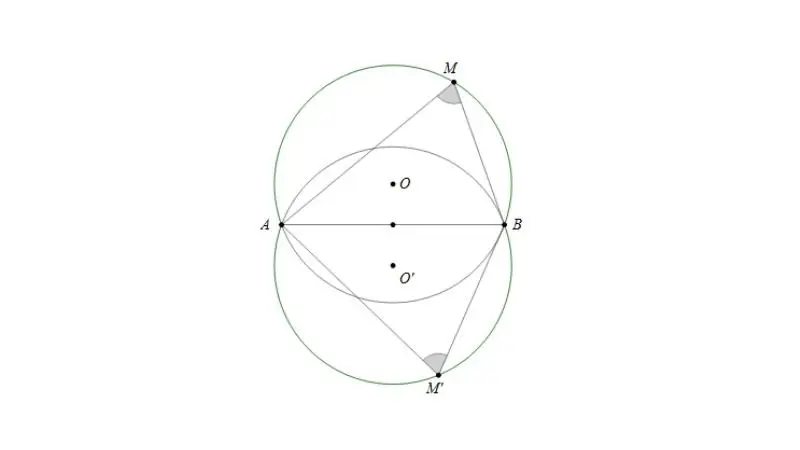
Hai cung chứa góc đối xứng nhau:

• Hai cung chứa góc đối xứng nhau qua tâm đường tròn có cùng số đo.

Ví dụ:

Cho đường tròn (O) và hai điểm A, B trên đường tròn.

• Cung \(\stackrel{\frown}{AmB}\) và cung \(\stackrel{\frown}{A’nB’}\)đối xứng nhau qua tâm O.
• Do đó, \(\stackrel{\frown}{AmB}\) = \(\stackrel{\frown}{A’nB’}\).

Góc nội tiếp và góc có đỉnh ở bên ngoài đường tròn:

Góc nội tiếp chắn một cung có số đo bằng nửa số đo của cung đó.

Góc có đỉnh ở bên ngoài đường tròn chắn hai cung có số đo bằng nửa hiệu số đo của hai cung đó.

Ví dụ:

Cho đường tròn (O) và hai điểm A, B trên đường tròn.

\(\angle AOB\) là góc nội tiếp chắn \(\stackrel{\frown}{AmB}\).

Do đó,\(\stackrel{\frown}{AmB}\) = 2\(\angle AOB\).

\(\angle ACB\) là góc có đỉnh ở bên ngoài đường tròn chắn hai \(\stackrel{\frown}{AmB}\) và \(\stackrel{\frown}{AnB}\) .

Do đó, sđ \(\stackrel{\frown}{AmB}\) – sđ \(\stackrel{\frown}{AnB}\) = 2\(\angle ACB\).

Số đo cung chứa góc

Số đo cung chứa góc là số đo của phần cung tròn được giới hạn bởi hai điểm A và B trên đường tròn, được ký hiệu là sđ \(\stackrel{\frown}{AB}\).

Có hai cách để xác định số đo cung chứa góc:

Dựa vào góc nội tiếp:

Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh của góc cắt đường tròn tại hai điểm khác nhau.

Số đo cung chứa góc bằng nửa số đo của góc nội tiếp chắn cung đó.

Ví dụ:

Cho đường tròn (O) và hai điểm A, B trên đường tròn.

• \(\angle AOB\) là góc nội tiếp chắn cung \(\stackrel{\frown}{AmB}\) .
• Do đó, sđ \(\stackrel{\frown}{AmB}\) = 2\(\angle AOB\).

Dựa vào hai cung đối xứng:

• Hai cung đối xứng nhau qua tâm đường tròn có cùng số đo.
• Do đó, ta có thể sử dụng số đo của một cung để xác định số đo của cung đối xứng.

Ví dụ:

Cho đường tròn (O) và hai điểm A, B trên đường tròn.

Cung \(\stackrel{\frown}{AmB}\) và cung \(\stackrel{\frown}{A’nB’}\)đối xứng nhau qua tâm O.

Do đó, sđ \(\stackrel{\frown}{AmB}\) = \(\stackrel{\frown}{A’nB’}\).

Công thức tính số đo cung:

Cung nhỏ: sđ \(\stackrel{\frown}{AB}\) = 2\(\angle AOB\)

Cung lớn: sđ \(\stackrel{\frown}{AB}\) = 360° – 2\(\angle AOB\)

Lưu ý:

• Số đo cung luôn được tính bằng độ.
• Số đo cung có thể là số nguyên hoặc số thập phân.

Ví dụ:

• Cho đường tròn (O) và hai điểm A, B trên đường tròn sao cho \(\angle AOB\) = 60°.
• Cung\(\stackrel{\frown}{AmB}\) là cung nhỏ.
• Do đó, sđ \(\stackrel{\frown}{AmB}\) = 2\(\angle AOB\) = 2 * 60° = 120°.
• Cho đường tròn (O) và hai điểm A, B trên đường tròn sao cho \(\angle AOB\) = 120°.
• Cung \(\stackrel{\frown}{AmB}\) là cung lớn.
• Do đó, sđ \(\stackrel{\frown}{AmB}\) = 360° – 2\(\angle AOB\) = 360° – 2 * 120° = 240°.

Các ứng dụng về cung chứa góc

Cung chứa góc có nhiều ứng dụng trong thực tế, bao gồm:

Tính độ dài cung:

Cho biết bán kính đường tròn R và số đo cung sđ \(\stackrel{\frown}{AB}\), ta có thể tính độ dài cung AB bằng công thức:

Độ dài cung AB = \(\frac{\overset{\frown}{AB}}{360^\circ} \times 2\pi R\)

Ví dụ:

Cho đường tròn (O) có bán kính R = 5cm và \(\stackrel{\frown}{AmB}\) có số đo sđ \(\stackrel{\frown}{AmB}\) = 120°. Tính độ dài cung \(\stackrel{\frown}{AmB}\).

Độ dài cung \(\stackrel{\frown}{AmB}\)= \(\frac{120^\circ}{360^\circ} \times 2\pi \times 5\,\text{cm} = 10\pi\,\text{cm}\)

Tính diện tích hình quạt:

• Cho biết bán kính đường tròn R và số đo cung sđ \(\stackrel{\frown}{AB}\), ta có thể tính diện tích hình quạt AOB bằng công thức:

Diện tích hình quạt AOB = \(\frac{\overset{\frown}{AB}}{360^\circ} \times \pi R^2\)

Ví dụ:

Cho đường tròn (O) có bán kính R = 5cm và cung AmB có số đo sđ \(\stackrel{\frown}{AmB}\) = 120°. Tính diện tích hình quạt AOB.

Diện tích hình quạt\(AOB = \frac{120^\circ}{360^\circ} \times \pi \times 5\,\text{cm}^2 = 25\pi\,\text{cm}^2\)

Vẽ các cung tròn:

Sử dụng compa để vẽ các cung tròn với độ dài và vị trí xác định.

 Chứng minh các tính chất của đường tròn:

Sử dụng tính chất của cung chứa góc để chứng minh các tính chất của đường tròn như:

• Hai đường tròn cắt nhau tại hai điểm thì hai cung bị chắn bởi hai điểm đó bằng nhau.
• Góc nội tiếp và góc có đỉnh ở bên ngoài đường tròn chắn hai cung.

Ứng dụng trong các lĩnh vực khác:

• Thiên văn học: Dùng để xác định vị trí của các hành tinh, sao chổi, …
• Kỹ thuật: Dùng để thiết kế các chi tiết máy móc, …
• Kiến trúc: Dùng để thiết kế các vòm, mái nhà, …

Ví dụ:

• Trong thiên văn học, cung chứa góc được sử dụng để xác định vị trí của các hành tinh, sao chổi, … trên bầu trời.
• Trong kỹ thuật, cung chứa góc được sử dụng để thiết kế các chi tiết máy móc như bánh răng, ròng rọc, …
• Trong kiến trúc, cung chứa góc được sử dụng để thiết kế các vòm, mái nhà, …

Như vậy, qua bài viết này, chúng ta đã tìm hiểu về khái niệm cung chứa góc và tầm quan trọng của nó. Việc học tập về cung chứa góc giúp học sinh giải quyết nhiều dạng toán liên quan đến đường tròn, đồng thời giúp học sinh phát triển tư duy logic và khả năng giải quyết vấn đề.