Vi phân là gì? Khái niệm, ý nghĩa và công thức tính vi phân đầy đủ
Vi phân là một khái niệm quan trọng trong chương trình Giải tích 12, đóng vai trò nền tảng cho nhiều chủ đề khác như đạo hàm, tích phân, ứng dụng trong hình học và vật lý.
Vi phân là một khái niệm quan trọng trong chương trình Giải tích 12, đóng vai trò nền tảng cho nhiều chủ đề khác như đạo hàm, tích phân, ứng dụng trong hình học và vật lý. Bài viết này sẽ cung cấp cho bạn kiến thức về vi phân và các ví dụ minh họa cụ thể để giúp bạn dễ dàng hiểu và áp dụng.
Vi phân là gì?
Vi phân là một nhánh của giải tích toán học tập trung vào việc nghiên cứu sự thay đổi của hàm số.
Nó liên quan đến việc tính toán tỷ lệ thay đổi của một hàm số tại một điểm cụ thể, được gọi là đạo hàm.
Cho hàm số y = f(x) xác định trên (a;b) và có đạo hàm tại x ∈ (a;b)
– Giả sử x là số gia của x sao cho x + x ∈ (a;b)
– Ta gọi f'(x). x là vì phân của hàm số y = f(x) tại x ứng với số gia x và kí hiệu là dy hoặc df(x) dy = df(x) = f'(x).x
Các dạng bài tập vi phân có ví dụ
Dạng toán tìm vi phân của hàm số y = f(x)
Phương pháp
Bước 1: Tính đạo hàm f'(x)
Bước 2: Tính vi phân của hàm số y = f(x) tại x là \(df(x) = f'(x)dx\)
Bước 3: Tính vi phân của hàm số y = f(x) tại xã là \(df(x) = f'(x)dx\)
Ví dụ
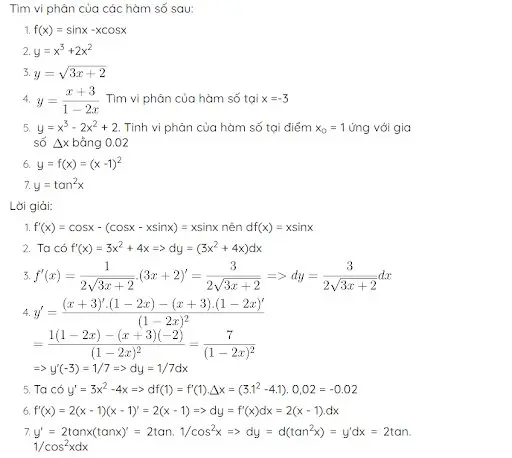
Dạng bài tìm giá trị gần đúng của một biểu thức
Phương pháp
Bước 1: Lập hàm số \(y = f(x)\) và chọn xo, Δx thích hợp
Bước 2: Tính đạo hàm f'(x), \(f(x_0)\) và \(f(x_0)\)
Bước 3: Tính giá trị gần đúng của biểu thức: \(P = f(x_0o +Δx) ≈ f(x_0) + f'(x_0).Δx\)
Ví dụ

Trắc nghiệm vi phân tự luyện
Câu 1: Cho hàm số \(f(x)=x2+2x+1\). Vi phân của hàm số tại điểm x0=1 là:
- dy=3dx
- dy=4dx
- dy=5dx
- dy=6dx
Câu 2: Tính giá trị gần đúng của 1.01
- 1.005
- 1.010
- 1.015
- 1.020
Câu 3: Cho hàm số \(f(x)=sin(x)\). Vẽ đồ thị hàm số bằng cách sử dụng vi phân.
- Đồ thị hàm số là một đường thẳng.
- Đồ thị hàm số là một đường parabol.
- Đồ thị hàm số là một đường sin.
- Đồ thị hàm số là một đường cos.
Câu 4: Một vật chuyển động với vận tốc \(v(t)=t2+2t−1 m/s\). Tính quãng đường đi được trong 3 giây đầu tiên.
- 4 m
- 5 m
- 6 m
- 7 m
Câu 5: Ứng dụng nào sau đây không liên quan đến vi phân?
- Tính gần đúng giá trị của hàm số
- Vẽ đồ thị hàm số
- Giải các bài toán liên quan đến tốc độ, gia tốc
- Giải các bài toán liên quan đến diện tích, thể tích
Bài tập tự luận
Câu 1: Cho hàm số \(f(x)=x^3+2x^2−1\). Tính vi phân của hàm số tại điểm x0=1.
Câu 2: Tính giá trị gần đúng của sin(0.1).
Câu 3: Vẽ đồ thị hàm số \(f(x)=x^2−4x+3\).
Câu 4: Một vật chuyển động với vận tốc \(v(t)=t^2−3t+1 m/s\). Tính quãng đường đi được trong 2 giây đầu tiên.
Hy vọng bài viết này đã cung cấp cho bạn kiến thức đầy đủ về vi phân.
Bên cạnh bài viết này, bạn có thể tham khảo thêm các tài liệu và bài giảng khác để củng cố kiến thức
Bài Viết Liên Quan
Với niềm đam mê mãnh liệt đối với toán học, tôi luôn mong muốn truyền tải kiến thức và khơi gợi niềm yêu thích môn học này cho thế hệ trẻ. Tôi luôn tận tâm trong công việc giảng dạy, sử dụng phương pháp giảng dạy sáng tạo và hiệu quả để giúp học sinh tiếp thu kiến thức một cách dễ dàng và hứng thú. Với những thành tựu xuất sắc trong lĩnh vực toán học, tôi đã nhận được nhiều giải thưởng danh giá và được cộng đồng khoa học đánh giá cao. Tôi là nguồn cảm hứng và tấm gương sáng cho các thế hệ học sinh và sinh viên yêu thích toán học.









