Khoảng cách từ một điểm đến một mặt phẳng là một khái niệm quan trọng trong hình học không gian lớp 11. Nó được ứng dụng trong nhiều bài toán liên quan đến tính toán, đo lường và giải quyết các vấn đề thực tế. Bài viết này sẽ trình bày các phương pháp để tính khoảng cách từ một điểm đến một mặt phẳng trong chương trình Toán lớp 11.
Định nghĩa khoảng cách từ một điểm đến một mặt phẳng
Cho điểm M và mặt phẳng (P) trong không gian. Khoảng cách từ điểm M đến mặt phẳng (P) là khoảng cách giữa hai điểm M và H, trong đó H là hình chiếu vuông góc của M lên mặt phẳng (P).
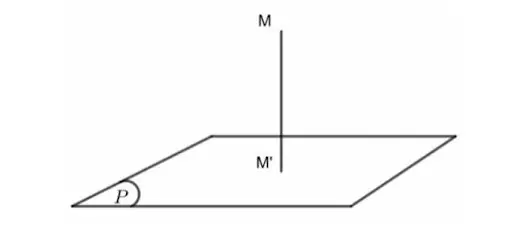
Công thức tính khoảng cách từ một điểm đến một mặt phẳng
Trong hệ tọa độ không gian Oxyz, cho điểm M có tọa độ như sau: (a; β; γ). Cho mặt phẳng (P) có phương trình dạng ax + by + cz + d = 0. Công thức tổng quát tính khoảng cách từ điểm m đến mặt phẳng (P) được
tính như sau:
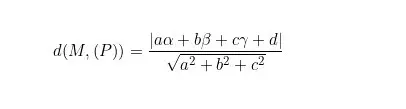
Các phương pháp tính khoảng cách từ điểm đến mặt phẳng
Phương pháp số 1: Dựa vào định nghĩa
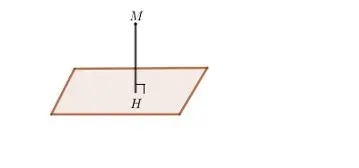
Theo đúng như định nghĩa, để tính được khoảng cách từ điểm M tới mặt phẳng (P) chúng ta sẽ tìm hình chiếu của M trên mặt phẳng (ta gọi là điểm H) rồi tính độ dài MH dựa trên công thức tính khoảng cách
Phương pháp số 2: Tính khoảng cách gián tiếp
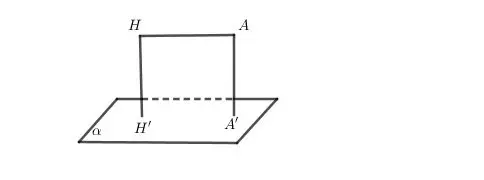
Ta tìm một điểm H’ sao cho đường thẳng đi qua M và H’ song song với mặt phẳng P. Vậy từ đó ta có thể suy ra được khoảng cách từ M đến mặt phẳng P bằng khoảng cách từ Hỉ đến P
d(M, (P)) = d(H’, (P))
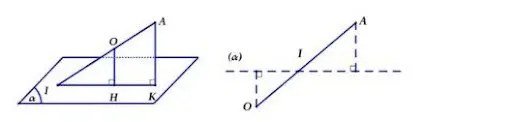
Phương pháp số 3: Sử dụng tam giác đồng dạng
Tìm 1 điểm O xác định, ta tìm giao điểm của OA với mặt phẳng (P) là I. Vậy ta tính khoảng cách từ d(O, (alpha))/d(A,(alpha)) = OI/AI (dựa theo định lý Ta-lét)
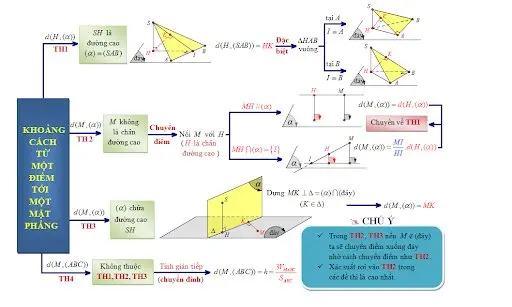
Sơ đồ tư duy khoảng cách từ một điểm tới mặt phẳng
Bài tập có lời giải chi tiết bài khoảng cách từ một điểm đến mặt phẳng
Bài tập 1
Cho lăng trụ đứng ABC.A’B’C’ với đáy là một tam giác vuông cân ABC với BC = BA = a, độ dài cạnh bên AA’ có kích thước là av2. Gọi trung điểm của đoạn thẳng BC là M, hãy tính khoảng cách giữa 2 đường thẳng AM với B’C’.
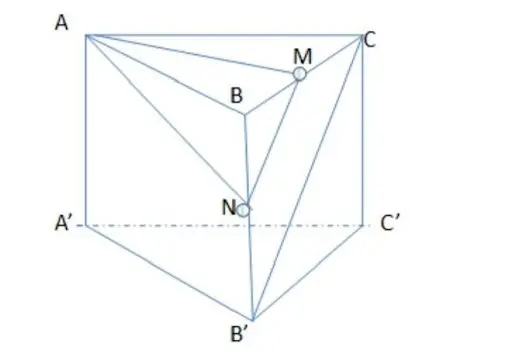
Giải
Gọi trung điểm của cạnh bên BB’ là N. Lúc này đoạn thẳng MN là đường trung bình của tam giác BB’C.
Suy ra: B’C song song MN => B’C song song với mặt phẳng (AMN)
Vậy ta có khoảng cách từ B’C đến mặt đến AM là d(B’C; AM) = d(B’C; (AMN)) = d(B’; (AMN))
Mà BB’ giao với mặt phẳng (AMN) tại điểm N, mà N là trung điểm của BB’.
Suy ra: d(B’; (AMN)) = d(B; (AMN))
Ta có: Hình chóp A.BMN có BA, BM và BN có một góc vuông
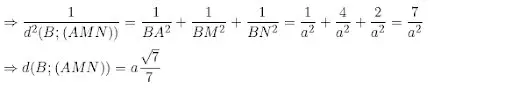
Việc nắm vững các phương pháp tính khoảng cách từ một điểm đến một mặt phẳng sẽ giúp học sinh giải quyết các bài toán liên quan một cách hiệu quả.
Ngoài ra, học sinh cần lưu ý một số trường hợp đặc biệt khi áp dụng các phương pháp này.
Chúc các bạn học tốt!
