Đường tròn – một biểu tượng vô cùng quen thuộc trong hình học, luôn ẩn chứa những bí ẩn kỳ diệu và tính chất đặc biệt, đặc biệt là tính chất đối xứng.
Từ những nền văn minh cổ đại đến hiện đại, khám phá về tính chất này đã mở ra những cánh cửa mới trong toán học và ứng dụng trong thực tế. Hãy cùng nhau khám phá những điều kì diệu của tính chất đối xứng trong hình học đường tròn.
Tính chất đối xứng tâm
Tính chất đối xứng tâm của đường tròn là một trong những đặc điểm cơ bản và quan trọng nhất của hình học đường tròn. Điều này ám chỉ rằng mọi điểm trên đường tròn đều có cùng một khoảng cách đến tâm của đường tròn.
Cụ thể, nếu A là một điểm bất kỳ trên đường tròn và O là tâm của đường tròn, thì khoảng cách từ điểm A đến O luôn là một giá trị không đổi. Khoảng cách này chính là bán kính của đường tròn.
Đặc điểm này không chỉ giúp ta hiểu về cách xác định tâm và bán kính của đường tròn mà còn quan trọng trong việc giải các bài toán liên quan đến hình học và cơ sở của nhiều phép toán trong toán học.
Đối với bất kỳ điểm nào trên đường tròn, tính chất đối xứng tâm giữ cho chúng cùng “đối xứng” với nhau quanh tâm, làm cho đường tròn trở thành một trong những hình dạng đối xứng đơn giản và quan trọng nhất trong hình học.
Chứng minh:
a) Hai điểm đối xứng qua tâm O đều cách đều tâm O.
- Gọi M là một điểm bất kỳ trên đường tròn (O; R).
- Lấy điểm M’ đối xứng với M qua tâm O.
- Ta có: OM = OM’ (tính chất đối xứng tâm)
- Do đó, hai điểm M và M’ cách đều tâm O.
b) Góc nội tiếp và góc tạo bởi tia và dây cung cùng chắn một cung có số đo bằng nhau.
- Gọi A và B là hai điểm bất kỳ trên đường tròn (O; R).
- Góc nội tiếp AOB là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai điểm A và B.
- Góc tạo bởi tia OA và dây cung AB là góc AOC.
- Ta có: góc AOB và góc AOC cùng chắn cung AB.
- Do đó, góc AOB = AOC (góc nội tiếp và góc tạo bởi tia và dây cung cùng chắn một cung có số đo bằng nhau).
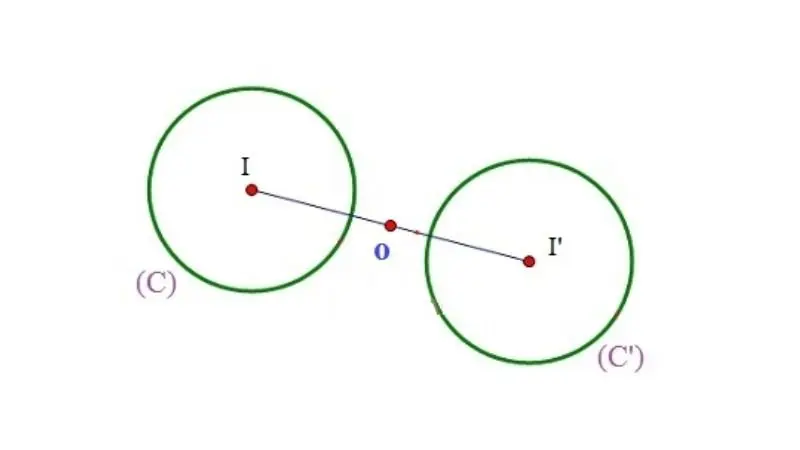
c) Hai đường tròn có tâm đối xứng qua một điểm thì có bán kính bằng nhau.
- Gọi O và O’ là hai tâm của hai đường tròn (O; R) và (O’; R’).
- Gọi I là điểm đối xứng của O qua O’.
- Ta có: OI = O’I (tính chất đối xứng tâm)
- Do đó, R = R’ (hai đường tròn có tâm đối xứng qua một điểm thì có bán kính bằng nhau).
Tính chất đối xứng trục
Tính chất đối xứng trục của đường tròn là một tính chất quan trọng khác, mô tả mối quan hệ giữa các điểm trên đường tròn và một đường thẳng chia đường tròn thành hai phần bằng nhau, đi qua tâm của đường tròn.
Cụ thể, nếu A là một điểm trên đường tròn và O là tâm của đường tròn, thì điểm đối xứng của A qua đường trục là một điểm A’ nằm ở phía đối diện của A qua tâm O. Điểm ‘A cũng có cùng khoảng cách với tâm O như điểm A. Điều này ngụ ý rằng mọi điểm trên đường tròn đều có một điểm đối xứng qua đường trục, và ngược lại.
Đặc điểm này rất hữu ích trong việc nghiên cứu và áp dụng hình học đường tròn. Nó giúp chúng ta xác định các điểm đối xứng nhằm tạo ra các hình dạng đối xứng hoặc giải quyết các bài toán hình học. Đồng thời, tính chất này còn đóng vai trò quan trọng trong nhiều lĩnh vực ứng dụng như thiết kế đồ họa, cơ khí, và điện tử.
Chứng minh
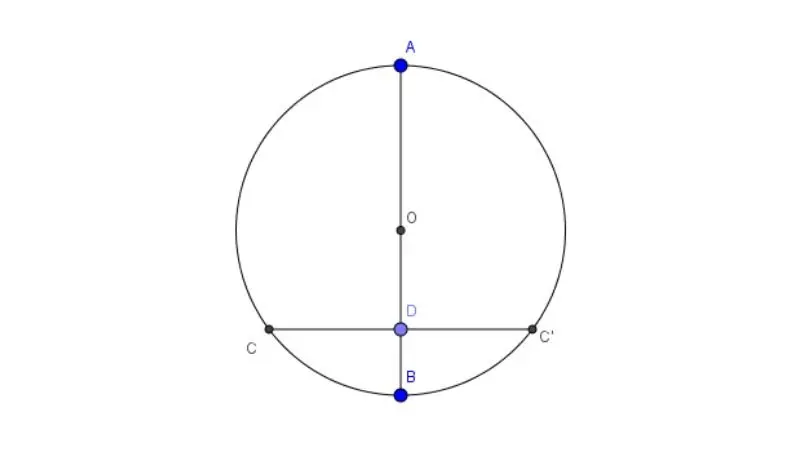
Hai điểm đối xứng qua đường kính AB đều cách đều đường kính AB.
- Gọi M là một điểm bất kỳ trên đường tròn (O; R).
- Lấy điểm M’ đối xứng với M qua đường kính AB.
- Ta có: MA = MA’ (tính chất đối xứng trục)
- Do đó, hai điểm M và M’ cách đều đường kính AB.
b) Góc nội tiếp và góc tạo bởi tia và dây cung cùng chắn một cung có số đo bằng nhau.
Gọi A và B là hai điểm bất kỳ trên đường tròn (O; R).
Góc nội tiếp AOB là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai điểm A và B.
Góc tạo bởi tia OA và dây cung AB là góc AOC.
Ta có: AOB và AOC cùng chắn cung AB.
Do đó,AOB=AOC(góc nội tiếp và góc tạo bởi tia và dây cung cùng chắn một cung có số đo bằng nhau).
c) Hai đường tròn có tâm đối xứng qua một điểm thì có bán kính bằng nhau.
- Gọi O và O’ là hai tâm của hai đường tròn (O; R) và (O’; R’).
- Gọi I là điểm đối xứng của O qua O’.
- Ta có: OI = O’I (tính chất đối xứng tâm)
- Do đó, R = R’ (hai đường tròn có tâm đối xứng qua một điểm thì có bán kính bằng nhau).
Tính chất đối xứng quay
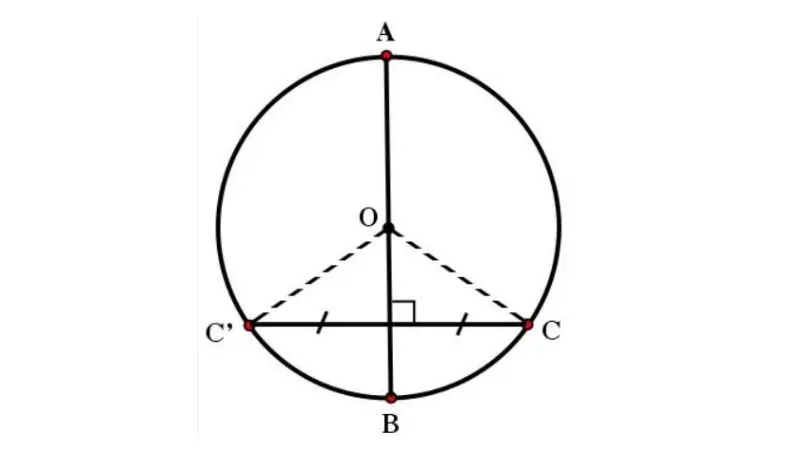
Tính chất đối xứng quay là một tính chất đặc biệt của đường tròn, chỉ xuất hiện ở các hình tròn hoàn hảo, trong đó mọi điểm trên đường tròn đều đối xứng với một điểm khác trên cùng đường tròn thông qua một phép quay xung quanh tâm của nó.
Cụ thể, nếu A là một điểm trên đường tròn và O là tâm của đường tròn, thì điểm đối xứng của A qua phép quay sẽ là một điểm A’ nằm trên đường tròn và cách tâm O một khoảng bằng với A, nhưng ở vị trí khác so với A dựa trên góc quay xung quanh tâm O.
Tính chất đối xứng quay không chỉ là một khía cạnh cơ bản trong hình học, mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực. Ví dụ, trong công nghệ, việc hiểu và áp dụng tính chất này là cực kỳ quan trọng trong việc thiết kế và lập trình các hệ thống máy móc, máy tính và cả trong thiết kế đồ họa. Đối xứng quay cũng đóng vai trò quan trọng trong việc giải các bài toán hình học phức tạp và trong nghiên cứu về toán học đại số.
Hệ quả tính chất đối xứng của đường tròn
Hệ quả của tính chất đối xứng tâm:
Tất cả các điểm trên đường tròn đều cách đều tâm O.
Góc nội tiếp và góc tạo bởi tia và dây cung cùng chắn một cung có số đo bằng nhau.
Hai đường tròn có tâm đối xứng qua một điểm thì có bán kính bằng nhau.
Hệ quả của tính chất đối xứng trục:
Hai điểm đối xứng qua đường kính AB đều cách đều đường kính AB.
Hai dây cung đối xứng qua đường kính AB có độ dài bằng nhau.
Hai góc nội tiếp đối xứng qua đường kính AB có số đo bằng nhau.
Hệ quả của tính chất đối xứng quay:
Tất cả các điểm trên đường tròn đều cách đều tâm O.
Góc nội tiếp và góc tạo bởi tia và dây cung cùng chắn một cung có số đo bằng nhau.
Hai đường tròn có tâm đối xứng qua một điểm thì có bán kính bằng nhau.
Ví dụ:
Cho đường tròn (O; R) và điểm A trên đường tròn. Lấy điểm A’ đối xứng với A qua tâm O. Chứng minh rằng OA = OA’.
Cho đường tròn (O; R) và đường kính AB. Lấy điểm M trên đường tròn. Lấy điểm M’ đối xứng với M qua AB. Chứng minh rằng MM’ = 2R.
Cho hai đường tròn (O; R) và (O’; R’) có tâm O và O’ đối xứng qua điểm I. Chứng minh rằng R = R’.
Tính chất đối xứng của đường tròn là một kiến thức quan trọng trong Toán lớp 9. Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích về chủ đề này. Chúc bạn học tập tốt và đạt kết quả cao!
