Khối tròn xoay là một khái niệm quan trọng trong toán học, được ứng dụng trong nhiều lĩnh vực như xây dựng, cơ khí, kiến trúc… Bài viết này sẽ giới thiệu về khái niệm khối tròn xoay, công thức tính thể tích, diện tích xung quanh và diện tích toàn phần của khối tròn xoay, đồng thời cung cấp một số bài tập minh họa để giúp bạn hiểu rõ hơn về chủ đề này.
Lý thuyết thể tích khối tròn xoay
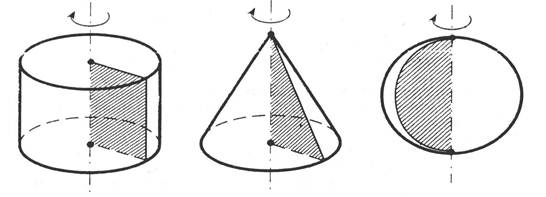
Khối tròn xoay là khối được tạo thành khi quay một hình phẳng quanh một trục cố định.
Thể tích khối tròn xoay là thể tích của phần không gian được giới hạn bởi mặt xung quanh và hai đáy của khối tròn xoay.
Công thức tính thể tích khối tròn xoay
\(V = \pi \int_{a}^{b} (f(x))^2 \, dx\)
trong đó:
V là thể tích của khối tròn xoay.
π là hằng số pi, xấp xỉ 3,14.
[a,b] là đoạn giới hạn của hình phẳng quay.
f(x) là hàm số biểu diễn đường cong giới hạn của hình phẳng quay.
Ví dụ:
Cho hình phẳng giới hạn bởi đường cong y = sinx, trục hoành và hai đường thẳng x = 0, x = π. Quay hình phẳng này quanh trục Ox ta được khối tròn xoay. Tính thể tích của khối tròn xoay.
Bài giải:
Thể tích của khối tròn xoay là:
\(V = \pi \int_{0}^{\pi} (\sin x)^2 \, dx = \pi \int_{0}^{\pi} (1 – \cos^2 x) \, dx = \pi [x – \frac{1}{2}\sin 2x] \Big|_{0}^{\pi} = \pi(\pi – 0) = \pi^2\)
Các dạng bài tập về thể tích khối tròn xoay
Dạng 1: Tính thể tích khối tròn xoay khi biết phương trình đường cong giới hạn và trục quay.
Phương pháp giải:
Áp dụng công thức tính thể tích khối tròn xoay:
\(V = \pi \int_{a}^{b} (f(x))^2 \, dx\)
trong đó:
V là thể tích của khối tròn xoay.
π là hằng số pi, xấp xỉ 3,14.
[a,b] là đoạn giới hạn của hình phẳng quay.
f(x) là hàm số biểu diễn đường cong giới hạn của hình phẳng quay.
Ví dụ:
Cho hình phẳng giới hạn bởi đường cong y = sinx, trục hoành và hai đường thẳng x = 0, x = π. Quay hình phẳng này quanh trục Ox ta được khối tròn xoay. Tính thể tích của khối tròn xoay.
Bài giải:
Thể tích của khối tròn xoay là:
\(V = \pi \int_{0}^{\pi} (\sin x)^2 \, dx = \pi \int_{0}^{\pi} (1 – \cos^2 x) \, dx = \pi \left[x – \frac{1}{2} \sin 2x \right] \bigg|_{0}^{\pi} = \pi(\pi – 0) = \pi^2\)
Dạng 2: Tính thể tích khối tròn xoay khi biết diện tích hình phẳng quay và khoảng cách từ trọng tâm của hình phẳng quay đến trục quay.
Phương pháp giải:
Áp dụng định lý Pappus-Guldin:
\(V = A.2πr\)
trong đó:
V là thể tích của khối tròn xoay.
A là diện tích hình phẳng quay.
r là khoảng cách từ trọng tâm của hình phẳng quay đến trục quay.
Ví dụ:
Cho hình phẳng giới hạn bởi đường cong y = x², trục hoành và hai đường thẳng x = 0, x = 2. Quay hình phẳng này quanh trục Ox ta được khối tròn xoay. Tính thể tích của khối tròn xoay.
Bài giải:
Diện tích hình phẳng quay là:
\(A = \int_{0}^{2} x^2 \, dx = \left[ \frac{x^3}{3} \right]_{0}^{2} = \frac{2^3}{3} – 0 = \frac{8}{3}\)
Trọng tâm của hình phẳng quay có tọa độ:
\((x̄, ȳ) = ((2/3), (\frac{1}{3}))\)
Khoảng cách từ trọng tâm của hình phẳng quay đến trục quay là:
\(r = ȳ = \frac{1}{3}\)
Thể tích của khối tròn xoay là:
\(V = A \cdot 2\pi r = \left( \frac{8}{3} \right) \cdot 2\pi \cdot \frac{1}{3} = \frac{16\pi}{9}\)
Dạng 3: Tính diện tích xung quanh, diện tích toàn phần của khối tròn xoay.
Phương pháp giải:
Diện tích xung quanh của khối tròn xoay bằng chu vi đường tròn giới hạn của hình phẳng quay nhân với chiều cao của khối tròn xoay.
Diện tích toàn phần của khối tròn xoay bằng diện tích xung quanh cộng với diện tích hai đáy.
Ví dụ:
Cho hình phẳng giới hạn bởi đường cong y = √x, trục Ox và hai đường thẳng x = 0, x = 4. Quay hình phẳng này quanh trục Ox ta được khối tròn xoay. Tính diện tích xung quanh và diện tích toàn phần của khối tròn xoay.
Bài giải:
Diện tích xung quanh của khối tròn xoay là:
\(Sxq = 2πr.h = 2π.√4.4 = 16π\)
Diện tích đáy của khối tròn xoay là:
\(B = πr² = π.4² = 16π\)
Diện tích toàn phần của khối tròn xoay là:
\(S_tp = S_xq + 2B = 16π + 2.16π = 48π\)
Bài tập về thể tích khối tròn xoay có lời giải
Bài 1:
Cho hình phẳng giới hạn bởi đường cong y = sinx, trục hoành và hai đường thẳng x = 0, x = π. Quay hình phẳng này quanh trục Ox ta được khối tròn xoay. Tính thể tích của khối tròn xoay.
Bài giải:
Thể tích của khối tròn xoay là:
\(V = \pi \int_{0}^{\pi} (\sin x)^2 \, dx = \pi \int_{0}^{\pi} (1 – \cos^2 2x) \, dx = \pi [x – \frac{1}{2} \sin 2x] \bigg|_{0}^{\pi} = \pi(\pi – 0) = \pi^2\)
Bài 2:
Cho hình phẳng giới hạn bởi đường cong y = x², trục hoành và hai đường thẳng x = 0, x = 2. Quay hình phẳng này quanh trục Ox ta được khối tròn xoay. Tính thể tích của khối tròn xoay.
Bài giải:
Diện tích hình phẳng quay là:
\(A = \int_{0}^{2} x^2 \, dx = \left[ \frac{x^3}{3} \right]_{0}^{2} = \frac{2^3}{3} – 0 = \frac{8}{3}\)
Trọng tâm của hình phẳng quay có tọa độ:
\((\bar{x}, \bar{y}) = \left(\frac{2}{3}, \frac{1}{3}\right)\)
Khoảng cách từ trọng tâm của hình phẳng quay đến trục quay là:
\(r = ȳ = \frac{1}{3}\)
Thể tích của khối tròn xoay là:
\(V = A \cdot 2\pi r = \left( \frac{8}{3} \right) \cdot 2\pi \cdot \frac{1}{3} = \frac{16\pi}{9}\)
Bài 3:
Cho hình phẳng giới hạn bởi đường cong y = √x, trục Ox và hai đường thẳng x = 0, x = 4. Quay hình phẳng này quanh trục Ox ta được khối tròn xoay. Tính diện tích xung quanh và diện tích toàn phần của khối tròn xoay.
Bài giải:
Diện tích xung quanh của khối tròn xoay là:
\(Sxq = 2πr.h = 2π.√4.4 = 16π\)
Diện tích đáy của khối tròn xoay là:
\(B = πr² = π.4² = 16π\)
Diện tích toàn phần của khối tròn xoay là:
\(S_tp = S_xq + 2B = 16π + 2.16π = 48π\)
Bài 4:
Tính thể tích phần chung của hai khối tròn xoay được tạo thành khi quay hình vuông ABCD cạnh a quanh trục Ox và Oy.
Bài giải:
Gọi O là tâm của hình vuông ABCD.
Khi quay hình vuông ABCD quanh trục Ox ta được khối trụ có bán kính đáy là \(\)R = \frac{a}{2} và chiều cao là h = a.
Khi quay hình vuông ABCD quanh trục Oy ta được khối trụ có bán kính đáy là \(\)R = \frac{a}{2} và chiều cao là h = a.
Thể tích phần chung của hai khối tròn xoay là thể tích của hình trụ có bán kính đáy là \(\)R = \frac{a}{2} và chiều cao là h = a.
Vậy, thể tích phần chung của hai khối tròn xoay là:
\(\)V = πR²h = π.(\frac{a}{2})²a = πa³/8
Như vậy, bài viết này đã giới thiệu về khái niệm khối tròn xoay, công thức tính thể tích, diện tích xung quanh và diện tích toàn phần của khối tròn xoay, đồng thời cung cấp một số bài tập minh họa. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức bổ ích về khối tròn xoay.
Chúc bạn học tốt với toanhoc.edu.vn








