Đường tròn – một hình dạng đơn giản nhưng mang trong mình sức mạnh vô cùng. Tính xác định của nó không chỉ được thể hiện trong toán học mà còn trong mọi khía cạnh của cuộc sống hàng ngày của chúng ta. Từ việc xây dựng kiến trúc đến công nghệ, từ nghệ thuật đến thiết kế, đường tròn không ngừng chứng minh vị thế và tầm quan trọng của mình.
Trên con đường khám phá sức mạnh của hình dạng này, chúng ta sẽ được chứng kiến những ứng dụng đa dạng và không ngừng mở ra những khả năng mới.
Định nghĩa đường tròn
Đường tròn là tập hợp các điểm trong mặt phẳng cách một điểm cố định (gọi là tâm) một khoảng cách không đổi (gọi là bán kính).
Có thể định nghĩa đường tròn theo các cách sau:
Đường tròn là quỹ tích các điểm cách một điểm cố định (tâm) một khoảng cách không đổi (bán kính).
Đường tròn là hình gồm các điểm cách tâm O một khoảng bằng R (R là bán kính).
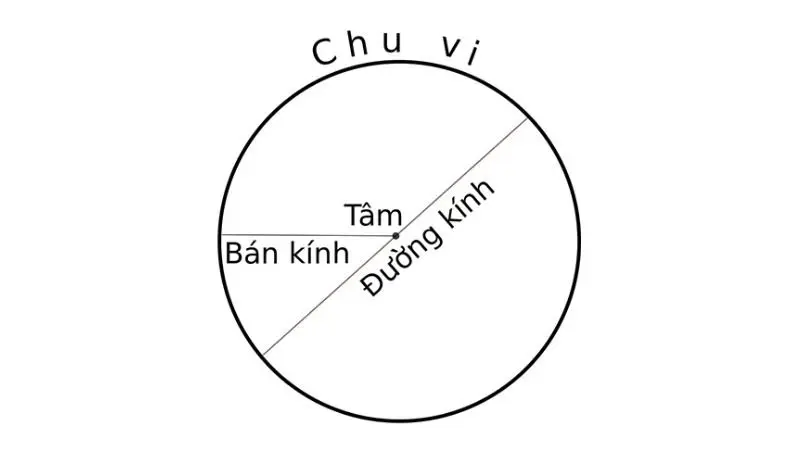
Thành phần của đường tròn:
- Tâm (O): Là điểm cố định nằm trong đường tròn.
- Bán kính (R): Là khoảng cách từ tâm đến bất kỳ điểm nào trên đường tròn.
- Đường kính (d): Là đoạn thẳng đi qua tâm và nối hai điểm trên đường tròn.
- Cung tròn: Là phần của đường tròn được giới hạn bởi hai điểm bất kỳ trên đường tròn.
- Dây cung: Là đoạn thẳng nối hai điểm bất kỳ trên đường tròn.
Tính chất của đường tròn:
- Tâm sai bằng 0: Đường tròn là một đường cong phẳng, khép kín và đối xứng qua tâm.
- Chu vi: Chu vi của đường tròn được tính theo công thức: C = 2πR.
- Diện tích: Diện tích hình tròn được tính theo công thức: S = πR².
- Góc nội tiếp: Góc nội tiếp trong đường tròn là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai điểm bất kỳ trên đường tròn.
- Góc tạo bởi tia và dây cung: Góc tạo bởi tia và dây cung là góc có đỉnh nằm trên đường tròn và hai cạnh chứa một tia và một dây cung.
Sự xác định của đường tròn
Xác định đường tròn bằng tâm và bán kính
Cho tâm O và bán kính R, ta có thể xác định đường tròn (O; R) theo các cách sau:
Sử dụng compa:
Bước 1: Đặt compa có độ mở bằng bán kính R.
Bước 2: Đặt mũi compa vào điểm O.
Bước 3: Vẽ một đường cong khép kín. Đường cong này chính là đường tròn (O; R).
Sử dụng phần mềm vẽ:
Bước 1: Mở phần mềm vẽ (ví dụ: Microsoft Paint, Adobe Illustrator,…).
Bước 2: Chọn công cụ vẽ đường tròn.
Bước 3: Nhập tâm O và bán kính R.
Bước 4: Vẽ đường tròn.
Sử dụng phương trình đường tròn:
Phương trình đường tròn có dạng:
\((x – a)^2 + (y – b)^2 = R^2\)Trong đó:
(a, b) là tọa độ tâm O.
R là bán kính.
Ví dụ: Cho tâm O(2, 3) và bán kính R = 5, phương trình đường tròn là:
\((x – 2)^2 + (y – 3)^2 = 5^2\)Xác định đường tròn bằng ba điểm không thẳng hàng
Cho ba điểm A, B, C không thẳng hàng, ta có thể xác định được một và chỉ một đường tròn đi qua ba điểm đó.
Cách xác định:
Dùng tính chất đường trung trực:
- Bước 1: Vẽ hai đường trung trực của đoạn thẳng AB và BC.
- Bước 2: Giao điểm của hai đường trung trực là tâm O của đường tròn.
- Bước 3: Vẽ đường tròn tâm O đi qua một trong ba điểm A, B, C.
Dùng tính chất đối xứng:
- Bước 1: Vẽ trung điểm M của AB.
- Bước 2: Vẽ đường thẳng d đi qua M và vuông góc với AB.
- Bước 3: Gọi O là điểm đối xứng của C qua đường thẳng d.
- Bước 4: Vẽ đường tròn tâm O đi qua một trong ba điểm A, B, C.
Dùng phương trình đường tròn:
- Bước 1: Chọn hệ trục tọa độ Oxy sao cho A, B, C có tọa độ.
- Bước 2: Viết phương trình đường tròn tâm O có bán kính R.
- Bước 3: Thay tọa độ của A, B, C vào phương trình đường tròn.
- Bước 4: Giải hệ phương trình để tìm R.
- Bước 5: Vẽ đường tròn tâm O với bán kính R.
Xác định đường tròn bằng đường kính
Cho đường kính AB, ta có thể xác định được đường tròn có đường kính AB theo các cách sau:
Dùng compa:
- Bước 1: Vẽ đoạn thẳng AB.
- Bước 2: Đặt compa có độ mở bằng 1/2 độ dài AB.
- Bước 3: Đặt mũi compa vào điểm A.
- Bước 4: Vẽ một đường cong khép kín. Đường cong này chính là đường tròn có đường kính AB.
Dùng phần mềm vẽ:
- Bước 1: Mở phần mềm vẽ (ví dụ: Microsoft Paint, Adobe Illustrator,…).
- Bước 2: Chọn công cụ vẽ đường tròn.
- Bước 3: Nhập độ dài đường kính AB.
- Bước 4: Vẽ đường tròn.
Dùng tính chất đường trung trực:
- Bước 1: Vẽ đường trung trực của đoạn thẳng AB.
- Bước 2: Tâm O của đường tròn là giao điểm của đường trung trực AB và đường vuông góc với AB tại trung điểm của AB.
- Bước 3: Vẽ đường tròn tâm O với bán kính bằng 1/2 độ dài AB.
Một số tính chất của đường tròn
Tính chất đối xứng:
Đường tròn có tâm O là hình có tính chất đối xứng tâm O.
Mọi đường kính của đường tròn đều là trục đối xứng của đường tròn.
Góc nội tiếp:
Góc nội tiếp trong đường tròn là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai điểm bất kỳ trên đường tròn.
Số đo của góc nội tiếp bằng nửa số đo của cung bị chắn bởi hai cạnh của góc.
Góc tạo bởi tia và dây cung:
Góc tạo bởi tia và dây cung là góc có đỉnh nằm trên đường tròn và hai cạnh chứa một tia và một dây cung.
Số đo của góc tạo bởi tia và dây cung bằng nửa số đo của cung bị chắn bởi dây cung và tia đó.
Góc nội tiếp và góc tạo bởi tia và dây cung:
Hai góc nội tiếp cùng chắn một cung có số đo bằng nhau.
Góc nội tiếp và góc tạo bởi tia và dây cung cùng chắn một cung có số đo bù nhau.
Hai đường tròn:
Hai đường tròn có tâm O và O’ được gọi là tiếp xúc nhau nếu và chỉ khi OO’ = R + R’, trong đó R và R’ là bán kính của hai đường tròn.
Hai đường tròn có tâm O và O’ được gọi là cắt nhau nếu và chỉ khi OO’ < R + R’.
Tính chất đặc biệt:
Đường tròn có chu vi và diện tích lớn nhất trong các hình phẳng có cùng chu vi.
Đường tròn là quỹ tích các điểm cách một điểm cố định (tâm) một khoảng cách không đổi (bán kính).
Như vậy, sự xác định của đường tròn không chỉ là một khái niệm toán học, mà còn là một phần không thể thiếu trong cuộc sống hàng ngày và trong nhiều lĩnh vực khác nhau. Tính quan trọng và ứng dụng rộng rãi của đường tròn đều chứng tỏ đây là một khái niệm mạnh mẽ và có ý nghĩa sâu sắc trong thế giới hiện đại.
