Hàm số lượng giác là một loại hàm số đặc biệt có liên quan đến các giá trị lượng giác của một góc. Bài viết này sẽ giúp bạn hiểu rõ hơn về khái niệm hàm số lượng giác, bao gồm các loại hàm số lượng giác cơ bản như sin, cos, tan, cot, tính chất của chúng và cách biểu diễn đồ thị của chúng.
Hàm số lượng giác là gì?
Các hàm lượng giác là các hàm toán học của góc, được dùng khi nghiên cứu tam giác và các hiện tượng có tính chất tuần hoàn. Các hàm lượng giác của một góc thường được định nghĩa bởi tỷ lệ chiều dài hai cạnh của tam giác vuông chứa góc đó, hoặc tỷ lệ chiều dài giữa các đoạn thẳng nối các điểm đặc biệt trên vòng tròn đơn vị.
- Hàm số sin:
Hàm số \(y = sinx\) được gọi là hàm số sin, với x là số thực. Tập xác định của hàm số sin là R.
- Hàm số cosin:
Hàm số \(y = cosx\) được gọi là hàm số cosin, với x là số thực. Tập xác định của hàm số cosin là R.
- Hàm số tang:
Hàm số \(y = tanx\) được gọi là hàm số tang, với \(x ≠ π/2 + kπ (k ∈ Z)\). Tập xác định của hàm số tang là \(R ∖ {π/2 + kπ | k ∈ Z}\).
- Hàm số cotang:
Hàm số \(y = cotx\) được gọi là hàm số cotang, với \(x ≠ kπ (k ∈ Z)\). Tập xác định của hàm số cotang là \(R ∖ {kπ | k ∈ Z}\).
Tính chất của hàm số lượng giác
Hàm số sin và cosin:
- Là hàm số tuần hoàn với chu kỳ 2π.
- Đều là hàm số chẵn.
- Đồng biến trên mỗi khoảng \((-2πk, -πk), (πk, 2πk) (k ∈ Z)\).
- Nghịch biến trên mỗi khoảng \((-πk, 0), (0, πk) (k ∈ Z)\).
Hàm số tang và cotang:
- Là hàm số tuần hoàn với chu kỳ π.
- Hàm số tang là hàm số lẻ.
- Hàm số cotang là hàm số chẵn.
- Đồng biến trên mỗi khoảng \((-π/2 + kπ, -π/4 + kπ), (π/4 + kπ, π/2 + kπ) (k ∈ Z)\).
- Nghịch biến trên mỗi khoảng \((-π/2 + kπ, -π/4 + kπ), (π/4 + kπ, π/2 + kπ) (k ∈ Z)\).
Bảng công thức lượng giác cần nhớ
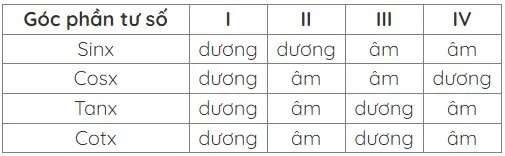
Bảng xét dấu của các giá trị lượng giác
Bài tập có lời giải cho hàm số lượng giác lớp 11
Dạng bài tập về tính chất
Bài tập 1:
Xác định chu kỳ, tập xác định, tập giá trị của hàm số \(y = sin(2x + π/3)\).
Lời giải:
- Chu kỳ của hàm số \(y = sinx là 2π\).
- Chu kỳ của hàm số \(y = sin(2x + π/3)\) là \(2π/2 = π\).
- Tập xác định của hàm số \(y = sinx\) là R.
- Tập giá trị của hàm số \(y = sinx là [-1, 1]\).
- Do đó, tập xác định của hàm số \(y = sin(2x + π/3)\) là R và tập giá trị là [-1, 1]
Bài tập 2:
Khảo sát sự đồng biến, nghịch biến của hàm số \(y = cos(x – π/4)\).
Lời giải:
Hàm số \(y = cos(x – π/4)\) có chu kỳ 2π.
Xét hàm số \(y = cosx\):
- Hàm số đồng biến trên các khoảng \((-2πk, -πk), (πk, 2πk) (k ∈ Z)\).
- Hàm số nghịch biến trên các khoảng \((-πk, 0), (0, πk) (k ∈ Z)\).
Do đó, hàm số \(y = cos(x – π/4)\) đồng biến trên các khoảng \((-2πk + π/4, -πk + π/4), (πk + π/4, 2πk + π/4) (k ∈ Z)\)
Hàm số \(y = cos(x – π/4)\) nghịch biến trên các khoảng \((-πk + π/4, 0 + π/4), (0 + π/4, πk + π/4) (k ∈ Z)\).
Dạng bài tập về phương trình lượng giác
Bài tập 3:
Giải phương trình \(sin2x = 1/2\).
Lời giải:
Phương trình sin2x = 1/2 có hai nghiệm:
- \(x = π/6 + 2kπ (k ∈ Z)\)
- \(x = 5π/6 + 2kπ (k ∈ Z)\)
Bài tập 4:
Giải phương trình \(cos2x + cosx – 1 = 0\).
Lời giải:
Đặt \(t = cosx\), ta được phương trình \(t^2 + t – 1 = 0\)
Phương trình này có hai nghiệm: t1 = 1 và t2 = -1.
Với t1 = 1, ta có cosx = 1, suy ra \(x = 2kπ (k ∈ Z)\).
Với t2 = -1, ta có cosx = -1, suy ra \(x = π + 2kπ (k ∈ Z)\).
Vậy, tập nghiệm của phương trình là \(S = {2kπ | k ∈ Z} ∪ {π + 2kπ | k ∈ Z}\).
Dạng bài tập về ứng dụng
Bài tập 5:
Một vật chuyển động điều hòa theo phương trình \(x = 2cos(10πt + π/3) (cm)\). Tìm vị trí của vật tại thời điểm t = 1/3 (s).
Lời giải:
Tại thời điểm t = 1/3 (s), ta có:
\(x = 2cos(10π * 1/3 + π/3) = 2cos(4π/3) = -1 cm\).
Vậy, tại thời điểm t = 1/3 (s), vật ở vị trí có x = -1 cm.
Hàm số lượng giác là một loại hàm số đặc biệt có liên quan đến các giá trị lượng giác của một góc. Bài viết này sẽ giúp bạn hiểu rõ hơn về khái niệm hàm số lượng giác, bao gồm các loại hàm số lượng giác cơ bản như sin, cos, tan, cot, tính chất của chúng và cách biểu diễn đồ thị của chúng.
