Góc có đỉnh ở bên ngoài đường tròn là một chủ đề quan trọng trong chương Hình học Tập 9. Kiến thức về loại góc này giúp học sinh giải quyết nhiều dạng toán liên quan đến đường tròn, như tính toán độ dài cung, diện tích hình quạt.
Bài viết này sẽ trình bày đầy đủ về định nghĩa, tính chất, cách vẽ và ứng dụng của góc có đỉnh ở bên ngoài đường tròn. Qua đó, giúp học sinh nắm vững kiến thức và tự tin giải quyết các bài toán liên quan.
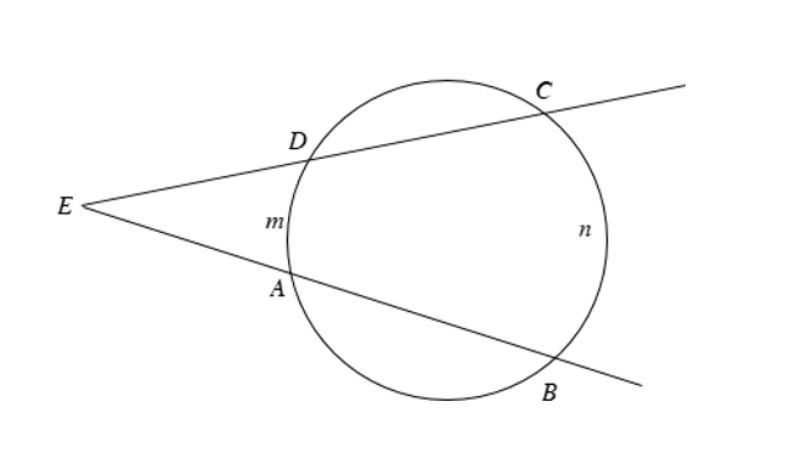
Định nghĩa góc có đỉnh bên ngoài đường tròn
Góc có đỉnh bên ngoài đường tròn được định nghĩa là góc tạo bởi hai tia cắt đường tròn, với đỉnh của góc nằm bên ngoài đường tròn. Cụ thể, góc này có các đặc điểm sau:
Đỉnh của góc không nằm trên đường tròn mà nằm ở bên ngoài.
Hai cạnh của góc cắt đường tròn tạo thành hai điểm giao nhau giữa mỗi cạnh và đường tròn.
Góc này có thể được tạo bởi:
- Hai dây cung: Khi cả hai cạnh của góc đều là dây cung của đường tròn, tức là mỗi cạnh cắt đường tròn tại hai điểm.
- Một dây cung và một tiếp tuyến: Khi một cạnh là dây cung cắt đường tròn tại hai điểm và cạnh kia là tiếp tuyến của đường tròn, chỉ chạm đường tròn tại một điểm.
- Hai tiếp tuyến: Khi cả hai cạnh của góc đều là tiếp tuyến của đường tròn, mỗi tiếp tuyến chỉ chạm đường tròn tại một điểm.
Số đo của góc có đỉnh bên ngoài đường tròn được tính bằng nửa hiệu số đo của cung lớn và cung nhỏ mà các cạnh của góc chắn hoặc tạo ra. Điều này giúp phản ánh mối quan hệ giữa góc và cấu trúc của đường tròn.
Định lý
Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
Giải thích:
Góc có đỉnh ở bên ngoài đường tròn: là góc có đỉnh nằm bên ngoài đường tròn và hai cạnh của góc đều cắt đường tròn tại hai điểm phân biệt.
Cung bị chắn: là cung nằm giữa hai cạnh của góc và nằm bên trong góc.
Chứng minh định lý:
Để chứng minh định lý trên, ta sẽ xét qua 3 trường hợp:
a) Mỗi cạnh của góc cắt đường tròn tại hai điểm phân biệt
Xét góc A có đỉnh ở bên ngoài đường tròn tâm O chắn hai cung \(\stackrel{\frown}{BD}\) và cung \(\stackrel{\frown}{CE}\). Ta cần chứng minh:
\(\angle A\) = \(\frac{\stackrel{\frown}{BD}\stackrel{\frown}{CE}}{2}\)
Ký hiệu và các cung như hình vẽ sau:
Ta có \(\angle D1\) là góc ngoài tại đỉnh D của tam giác ADC nên:
\(\angle D1\) =\(\angle C + \angle A \Rightarrow \angle A = \angle D1 – \angle C\) (1)
Lại có:
- \(\angle D1\) là góc nội tiếp chắn \(\stackrel{\frown}{CmE}\)=> \(\angle D1\) = \(\frac{1}{2}\) \(\stackrel{\frown}{CmE}\).
- \(\angle C1\) là góc nội tiếp chắn [/latex] \(\stackrel{\frown}{BnD}\) => \(\angle C\) = \(\frac{1}{2}\) \(\stackrel{\frown}{BnD}\)
Thay vào (1) ta được:
\(\angle A\) = \(\frac{1}{2}\) \(\stackrel{\frown}{CmE}\) – \(\frac{1}{2}\) \(\stackrel{\frown}{BnD}\)
=>\(\angle A\) = \(\frac{\stackrel{\frown}{CmE} – \stackrel{\frown}{BnD}}{2}\)
Vậy \(\angle A\) =\(\frac{\stackrel{\frown}{BD} – \stackrel{\frown}{CE}}{2}\)
(ĐPCM)
b) Một cạnh của góc tiếp tuyến của đường tròn
Xét góc A có đỉnh ở bên ngoài đường tròn tâm O và một cạnh AB là tiếp tuyến chắn hai cung \(\stackrel{\frown}{CD}\) và cung \(\stackrel{\frown}{BD}\) . Ta cần chứng minh:
\(\angle A\) = \(\frac{\stackrel{\frown}{CB} + \stackrel{\frown}{BD}}{2}\)
Ký hiệu và các cung như hình vẽ sau:
Ta có \(\angle C1\) là góc ngoài tại đỉnh C của tam giác ADC nên:
\(\angle C1\) = \(\angle A + \angle B \Rightarrow \angle A = \angle C_1 – \angle B\) (2)
Lại có: \(\angle C1\) là góc nội tiếp chắn \(\stackrel{\frown}{BmD}\) => \(\angle C1\) =\(\frac{1}{2}\)\(\stackrel{\frown}{BnD}\)
\(\angle B\) là góc tạo bởi tiếp tuyến BA và dây cung \(\stackrel{\frown}{BC}\) chắn cung \(\stackrel{\frown}{BnC}\) => \(\angle B\) = \(\frac{1}{2}\)\(\stackrel{\frown}{BnC}\).
Thay vào (2) ta được:
\(\angle A\) = \(\frac{1}{2}\)\(\stackrel{\frown}{BmD}\) – \(\frac{1}{2}\)\(\stackrel{\frown}{BnC}\)
=> \(\angle A\) = \(\frac{\stackrel{\frown}{BmD} – \stackrel{\frown}{BnC}}{2}\)
Vậy \(\angle A\) = \(\frac{\stackrel{\frown}{CB} – \stackrel{\frown}{BD}}{2}\) (ĐPCM)
c) Hai cạnh của góc là hai tiếp tuyến của đường tròn
Xét \(\angle A\) có đỉnh ở bên ngoài đường tròn tâm O và hai cạnh là hai tiếp tuyến của đường tròn tâm O. Ký hiệu và các cung như hình vẽ sau:
Khi đó \(\angle A\) chắn cung \(\stackrel{\frown}{BmC}\) và cung nhỉ \(\stackrel{\frown}{BnC}\). Ta cần chứng minh:
\(\angle A\)= \(\frac{\stackrel{\frown}{BC} – \stackrel{\frown}{BC}}{2}\)
Ta có \(\angle B1\) là góc ngoài tại đỉnh C của tam giác ADC nên:
\(\angle B_1 = \angle C_1 + \angle A \Rightarrow \angle A = \angle B_1 – \angle C_1\) (3)
Lại có:
- \(\angle B1\) là góc tạo bởi tiếp tuyến Bt và dây cung chắn cung lớn \(\stackrel{\frown}{BmC}\)
=> \(\angle B1\) = \(\frac{1}{2}\)\(\stackrel{\frown}{BmC}\)..
\(\angle C1\) là góc tạo bởi tiếp tuyến CA và dây cung \(\stackrel{\frown}{CB}\) chắn cung nhỏ \(\stackrel{\frown}{CnB}\)
=> \(\angle C1\) = \(\frac{1}{2}\)\(\stackrel{\frown}{CnB}\)..
Thay vào (3) ta được:
\(\angle A\) = \(\frac{1}{2}\)\(\stackrel{\frown}{BmC}\). – \(\frac{1}{2}\)\(\stackrel{\frown}{CnB}\).
=> \(\angle A\) = \(\frac{\stackrel{\frown}{BmC} – \stackrel{\frown}{CnB}}{2}\)
Vậy \(\angle A\)= \(\frac{\stackrel{\frown}{BC} – \stackrel{\frown}{BC}}{2}\) (ĐPCM)
Tính chất
Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
Góc tạo bởi hai tiếp tuyến
Khi hai tiếp tuyến từ một điểm nằm ngoài đường tròn tiếp xúc với đường tròn tại hai điểm, góc tạo bởi hai tiếp tuyến đó được gọi là góc tiếp tuyến. Tính chất của góc này là số đo của góc tiếp tuyến bằng nửa số đo của cung nằm giữa hai điểm tiếp xúc trên đường tròn.
Góc tạo bởi một tiếp tuyến và một dây cung
Khi một tiếp tuyến và một dây cung từ một điểm bên ngoài đường tròn tạo thành một góc, số đo của góc này bằng nửa số đo của cung lớn bị chắn bởi dây cung đó, trừ đi số đo của cung nhỏ đối diện.
Góc tạo bởi hai dây cung
Khi hai dây cung từ một điểm bên ngoài đường tròn tạo thành một góc, số đo của góc này bằng nửa hiệu số đo của cung lớn và cung nhỏ mà hai dây cung đó chắn.
Góc tạo bởi hai cát tuyến
Khi hai cát tuyến từ một điểm bên ngoài đường tròn tạo thành một góc, số đo của góc này bằng nửa hiệu số đo của hai cung mà hai cát tuyến đó chắn.
Những tính chất này rất hữu ích trong việc giải quyết các bài toán liên quan đến đường tròn, giúp xác định mối quan hệ giữa góc và cung trên đường tròn, cũng như giữa các yếu tố hình học khác nhau.
* Hai góc có đỉnh ở bên ngoài đường tròn cùng chắn hai cung bằng nhau thì bằng nhau.
Chứng minh
Phương pháp chứng minh:
Có hai phương pháp chính để chứng minh góc có đỉnh ở bên ngoài đường tròn:
- Phương pháp 1: Sử dụng định nghĩa và tính chất của góc có đỉnh ở bên ngoài đường tròn.
- Phương pháp 2: Sử dụng các tính chất của đường tròn và các góc liên quan.
Ví dụ:
Chứng minh:
\(\angle BAC\) là góc có đỉnh ở bên ngoài đường tròn (O).
Giải:
Phương pháp 1:
- \(\angle BAC\) có đỉnh B nằm bên ngoài đường tròn (O) và hai cạnh AB, AC cắt đường tròn tại hai điểm A, C.
- Theo định nghĩa, \(\angle BAC\) là góc có đỉnh ở bên ngoài đường tròn.
Phương pháp 2:
- Ta có: \(\angle BAC = \angle BOC + \angle COA\) (1)
- Do BC là dây cung của đường tròn (O) nên \(\angle BOC\) là góc nội tiếp chắn \(\stackrel{\frown}{BC}\).
- Do AC là dây cung của đường tròn (O) nên \(\angle COA\) là góc nội tiếp chắn \(\stackrel{\frown}{AC}\).
- Theo tính chất góc nội tiếp, ta có:
- \(\angle BOC\) = \(\frac{1}{2}\)\(\stackrel{\frown}{BC}\) (2)
- \(\angle COA\) = \(\frac{1}{2}\)\(\stackrel{\frown}{AC}\) (3)
- Thay (2) và (3) vào (1), ta được:
\(\angle BAC\) = \(\frac{1}{2}\)\(\stackrel{\frown}{AC}\) + \(\stackrel{\frown}{BC}\)
- Do \(\angle BAC\) là góc có đỉnh ở bên ngoài đường tròn (O) chắn hai cung\(\stackrel{\frown}{AC}\) và \(\stackrel{\frown}{BC}\) nên theo tính chất, ta có:
\(\angle BAC\) = \(\frac{1}{2}\)\(\stackrel{\frown}{AC}\) – \(\stackrel{\frown}{BC}\)
- Từ hai kết luận trên, ta có: \(\frac{1}{2}\)\(\stackrel{\frown}{AC}\) + \(\stackrel{\frown}{BC}\) = \(\frac{1}{2}\)\(\stackrel{\frown}{AC}\) – \(\stackrel{\frown}{BC}\)
- Vậy, \(\angle BAC\) là góc có đỉnh ở bên ngoài đường tròn (O).
Kết luận:
Có thể sử dụng hai phương pháp để chứng minh góc có đỉnh ở bên ngoài đường tròn. Việc lựa chọn phương pháp nào phụ thuộc vào điều kiện bài toán và khả năng của học sinh.
Bài tập liên quan
Dạng 1:
Tính số đo của góc có đỉnh ở bên ngoài đường tròn biết số đo hai cung bị chắn.
Ví dụ:
Cho đường tròn (O) và hai điểm A, B trên đường tròn. Biết sđ \(\stackrel{\frown}{AC}\) = \(120^\circ\) và sđ \(\stackrel{\frown}{BC}\) = \(60^\circ\). Tính số đo góc ACB.
Giải:
- \(\angle ABC\) là góc có đỉnh ở bên ngoài đường tròn (O) chắn hai \(\stackrel{\frown}{AC}\) và \(\stackrel{\frown}{BC}\).
- Theo tính chất, ta có: \(\angle ABC\) = \(\frac{1}{2}\)\(\stackrel{\frown}{AC}\) – \(\stackrel{\frown}{BC}\) = \(\frac{1}{2}\)\(120^\circ\) – \(60^\circ\) = \(60^\circ\)
Dạng 2:
Chứng minh một góc là góc có đỉnh ở bên ngoài đường tròn.
Ví dụ:
Cho đường tròn (O) và hai điểm A, B trên đường tròn. Gọi M là điểm chính giữa cung AB. Nối AM và BM. Chứng minh \(\angle AMB\) là góc có đỉnh ở bên ngoài đường tròn.
Giải:
- Ta có: \(\angle AMB\) = \(\angle AOM\) + \(\angle BMO\)
- Do AM là dây cung của đường tròn (O) nên \(\angle AOM\) là góc nội tiếp chắn \(\stackrel{\frown}{AM}\).
- Do BM là dây cung của đường tròn (O) nên \(\angle BMO\) là góc nội tiếp chắn cung \(\stackrel{\frown}{BM}\).
- Theo tính chất góc nội tiếp, ta có:
- \(\angle AOM\) = \(\frac{1}{2}\)\(\stackrel{\frown}{AM}\)
- \(\angle BMO\) = \(\frac{1}{2}\)\(\stackrel{\frown}{BM}\)
- Do M là điểm chính giữa cung \(\stackrel{\frown}{AB}\) nên \(\stackrel{\frown}{AM}\)= \(\stackrel{\frown}{BM}\)
Thay vào kết luận trên, ta được:
\(\angle AMB\)= \(\frac{1}{2}\)\(\stackrel{\frown}{AM}\) + \(\stackrel{\frown}{BM}\)
Vậy, \(\angle AMB\) là góc có đỉnh ở bên ngoài đường tròn (O) chắn hai cung \(\stackrel{\frown}{AM}\) và \(\stackrel{\frown}{BM}\).
Tóm lại, góc có đỉnh ở bên ngoài đường tròn là một chủ đề quan trọng và có nhiều ứng dụng trong thực tế. Việc nắm vững kiến thức về loại góc này giúp học sinh giải quyết các bài toán liên quan đến đường tròn một cách hiệu quả.