Tổng hợp kiến thức về đường tiệm cận

Đường tiệm cận là đường thẳng mà đồ thị hàm số tiến dần đến khi x tiến đến vô cùng hoặc đến một giá trị nào đó.

Có hai loại đường tiệm cận: tiệm cận ngang và tiệm cận đứng.

Tiệm cận giúp ta hiểu rõ hơn về hành vi của đồ thị hàm số khi x tiến đến vô cùng hoặc đến một giá trị nào đó.

Lý thuyết đường tiệm cận lớp 12

Định nghĩa

• Đường tiệm cận ngang: Đường thẳng y=y0​ được gọi là đường tiệm cận ngang của đồ thị hàm số y=f(x) nếu:
  • f(x) xác định trên một khoảng (a;+∞) hoặc (−∞;b) hoặc (−∞;+∞) với a,b là số thực.
  • Limxx→+∞​f(x)=y0​ hoặc Limxx→-∞​​f(x) = y0​.
• Đường tiệm cận đứng: Đường thẳng x = x0​ được gọi là đường tiệm cận đứng của đồ thị hàm số y=f(x) nếu:
  • f(x) xác định trên một khoảng (a;x0​) hoặc (x0​​;b) với a,b là số thực và a x0​​,b x0​​.
  • limx→x0+​​​f(x)=+∞ hoặc limx→x0-​​f(x)=−∞ hoặclimx→x0+​​f(x)=−∞ hoặc limx→x0-​​​f(x)=+∞.
• Đường tiệm cận xiên: Đường thẳng y=mx+n được gọi là đường tiệm cận xiên của đồ thị hàm số y=f(x) nếu:
  • f(x) xác định trên một khoảng (a;+∞) hoặc (−∞;b) hoặc (−∞;+∞) với a,b là số thực.
  • Limxx→+∞​[f(x)−(mx+n)]=0 hoặc Limxx→-∞​[f(x)−(mx+n)]=0.

2. Cách tìm:

• Tìm đường tiệm cận ngang:
  Tìm Limxx→+∞f(x) và Limxx→-∞​f(x).
  • Nếu Limxx→+∞​f(x)=y0​​ hoặc Limxx→-∞f(x)=y0​​ thì đường thẳng y=y0​​​ là đường tiệm cận ngang của đồ thị hàm số.
• Tìm đường tiệm cận đứng:
  • Xác định các điểm x0​ mà f(x) không xác định.
  • Tìm limx→x0+​​f(x), Limxx→-∞​​f(x), limx→x0+​​[f(x)−(mx+n)], Limxx→-∞Limxx→-∞​​[f(x)−(mx+n)].
  • Nếu limx→x0+​​f(x)=+∞ hoặc Limxx→-∞​​f(x)=−∞ hoặc limx→x0+​​f(x)=−∞ hoặc Limxx→-∞​​f(x)=+∞ thì đường thẳng x=x0 là đường tiệm cận đứng của đồ thị hàm số.
• Tìm đường tiệm cận xiên:
  • Chuyển vế để đưa hàm số về dạng y=mx+n+a(x)b(x) với a(x) và b(x) là đa thức.
  • Tìm Limxx→+∞​a(x)/ b(x)​ và Limxx→-∞​a(x) / b(x)
  • Nếu Limxx→+∞​a(x) / b(x)​=0 hoặc Limxx→-∞​a(x) / b(x)​=0 thì đường thẳng y=mx+n là đường tiệm cận xiên của đồ thị hàm số.

Một số kĩ năng để sử dụng máy tính

Ý tưởng giả sử cần tính lim f(x) ta dùng chức năng CALC để tính giá trị của f(x) tại các giá trị của x rất gần a.

Giới hạn của hàm số tại một điểm

lim f(x)x->a+ thì ta nhập f(x) và CALC x = a + 10^-9

lim f(x)x->a- thì ta nhập f(x) và CALC x = a – 10^-9

lim f(x)x->a thì ta sẽ nhập f(x) và CALC x = a + 10^-9 hoặc x = a – 10^-9

Giới hạn của hàm số tại vô cực

Limxx→+∞ thì ta sẽ nhập f(x) và CALC x = 10^10.

Limxx→-∞ thì ta sẽ nhập f(x) và CALC x = -10^10.

Bài tập tham khảo có lời giải

Bài 1:

 Tiệm cận đứng của đồ thị hàm số y = (x+1) / (x-2)  là đường thẳng có phương trình:

A. x = -1 .                    B. x = -2.              C. x = 2                     D. x = 1

Lời giải

Ta có:

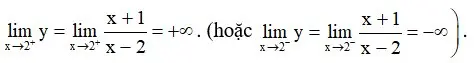
Vậy x = 2 là tiệm cận đứng của đồ thị hàm số.

Bài 2: Cho hàm số xác định và liên tục trên có bảng biến thiên như sau:

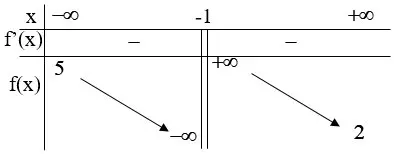
Khẳng định nào sau đây là khẳng định đúng? 

A. Đồ thị hàm số có một đường tiệm cận. 

B. Đồ thị hàm số có hai đường tiệm cận.

C. Đồ thị hàm số có hai TCN và một TCĐ  

D. Đồ thị hàm số có bốn đường tiệm cận.

Lời giải

Từ bảng biến thiên, ta có:

Chọn C.

Bài 3: Cho hàm số y = f(x) = số y = f(x) = 2x -3 / x +2. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm

Lời giải

Vì lim Yx->-∞  = 2; Yx->+∞ + = 2 nên đồ thị hàm số có 1 tiệm cận ngang là y = 2. 

Vi lim yx-> -2+= – ; lim yx->-2- = + nên đồ thị hàm số có 1 tiệm cận đứng x = -2. 

Do đó đồ thị hàm số có tổng số 2 tiệm cận kể cả đứng và ngang.

Bài tập tự giải

Bài 1: Cho hàm số số y= f(x)= 2x-5 / |x|-2. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm  y = f(x).

Bài 2: Cho hàm số y = f(x) có bảng biến thiên:

Tìm hàm tiệm cận của đồ thị hàm số y = 1f(x)?

Bài 3:Cho hàm số y = f(x) liên tục trên R \ {1} và có bảng biến thiên như sau

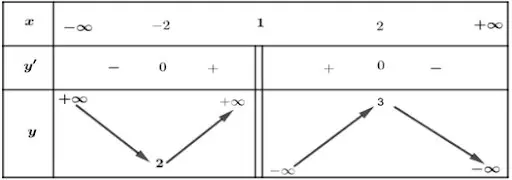
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = g(x) = f(x²-2x-2).

Ngoài các kiến thức đã học, còn có nhiều vấn đề liên quan đến đường tiệm cận cần được nghiên cứu thêm.

Hy vọng bài học này đã kích thích hứng thú của bạn với chủ đề đường tiệm cận.