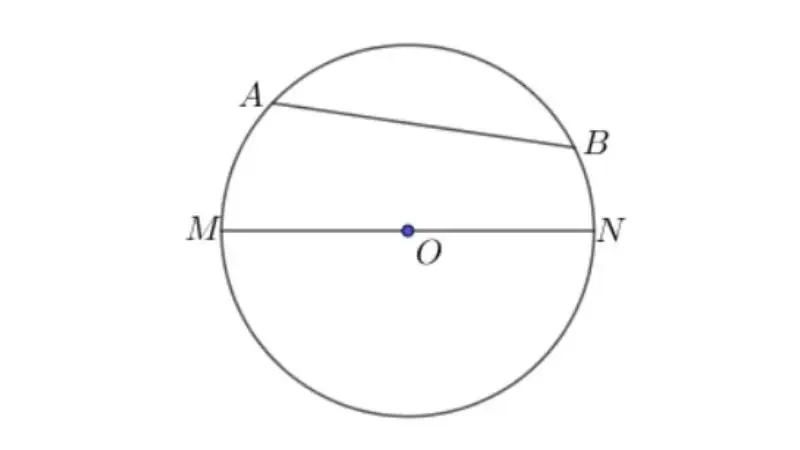
Lý thuyết về đường kính và dây của đường tròn - Toán lớp 9
Đường kính và dây của đường tròn là một chủ đề quan trọng trong chương "Hình học phẳng" của Toán lớp 9. Hiểu rõ về các khái niệm, tính chất và mối liên hệ giữa đường kính và dây của đường tròn sẽ giúp bạn giải quyết các bài toán liên quan một cách dễ dàng và chính xác.
Khi nói đến hình học đường tròn, hai khái niệm không thể không nhắc đến là đường kính và dây. Lý thuyết về đường kính và dây của đường tròn không chỉ là những khái niệm cơ bản mà còn là nền tảng của nhiều bài toán và ứng dụng trong toán học thực tiễn. Hãy cùng khám phá sâu hơn về hai khái niệm này và tìm hiểu về vai trò quan trọng của chúng trong thế giới của hình học đường tròn.
Đường kính
Định nghĩa:
Đường kính là đoạn thẳng đi qua tâm đường tròn và có hai đầu mút nằm trên đường tròn.
Tính chất:
Đường kính là dây cung lớn nhất trong đường tròn.
Độ dài đường kính gấp đôi bán kính: d = 2R.
Đường kính đi qua tâm đường tròn.
Hai điểm đối xứng qua đường kính thì cách đều đường kính.
Hệ quả:
Góc nội tiếp và góc tạo bởi tia và dây cung cùng chắn một cung có số đo bằng nhau.
Hai dây cung đối xứng qua đường kính thì có độ dài bằng nhau.
Hai góc nội tiếp đối xứng qua đường kính thì có số đo bằng nhau.
Ví dụ:
Cho đường tròn (O; R) và điểm A trên đường tròn. Lấy điểm A’ đối xứng với A qua tâm O. Chứng minh rằng OA = OA’.
Cho đường tròn (O; R) và đường kính AB. Lấy điểm M trên đường tròn. Lấy điểm M’ đối xứng với M qua AB. Chứng minh rằng MM’ = 2R.
Dây đường tròn
Định nghĩa:
Dây cung là đoạn thẳng nối hai điểm bất kỳ trên đường tròn.
Tính chất:
- Dây cung càng gần tâm đường tròn thì độ dài càng lớn.
- Dây cung đi qua tâm đường tròn là đường kính.
- Hai dây cung bằng nhau thì cách đều tâm đường tròn.
- Góc nội tiếp và góc tạo bởi tia và dây cung cùng chắn một cung có số đo bằng nhau.
Hệ quả:
- Hai điểm đối xứng qua đường kính thì cách đều đường kính.
- Hai dây cung đối xứng qua đường kính thì có độ dài bằng nhau.
- Hai góc nội tiếp đối xứng qua đường kính thì có số đo bằng nhau.
Ví dụ:
- Cho đường tròn (O; R) và điểm A trên đường tròn. Lấy điểm A’ đối xứng với A qua tâm O. Chứng minh rằng OA = OA’.
- Cho đường tròn (O; R) và đường kính AB. Lấy điểm M trên đường tròn. Lấy điểm M’ đối xứng với M qua AB. Chứng minh rằng MM’ = 2R.
Tính chất chung và đường kính và dây đường tròn
Đường kính và dây cung đều có thể chia đường tròn thành hai phần.
Đường kính và dây cung đều có thể được sử dụng để xác định vị trí của một điểm trên đường tròn.
| Tính chất | Đường kính | Dây cung |
| Độ dài | Lớn nhất trong các dây cung | Có thể có độ dài bất kỳ |
| Vị trí | Luôn đi qua tâm đường tròn | Có thể nằm ở bất kỳ vị trí nào trên đường tròn |
| Góc nội tiếp | Góc nội tiếp chắn bởi đường kính có số đo bằng 180° | Góc nội tiếp chắn bởi dây cung có số đo bằng nửa số đo cung bị chắn |
Hệ quả về đường kính và dây đường tròn
Hệ quả về đường kính và dây của đường tròn là một trong những khía cạnh quan trọng của hình học đường tròn. Cụ thể, mối liên hệ giữa đường kính và dây của đường tròn có thể được biểu diễn qua một số quy tắc và công thức toán học:
Quy tắc đường kính – dây: Đường kính của đường tròn luôn lớn hơn hoặc bằng dây của nó. Trong mọi trường hợp, đường kính của đường tròn luôn là giới hạn trên cho dây tương ứng.
Công thức tính dây của đường tròn: Dây của đường tròn có thể được tính toán bằng cách sử dụng công thức d=π×r×θ, trong đó d là độ dài của dây, r là bán kính của đường tròn và θ là góc tương ứng mà dây cắt ra từ tâm của đường tròn.
Công thức tính đường kính từ dây: Nếu biết độ dài của dây và bán kính của đường tròn, ta có thể tính toán đường kính bằng công thức D = π / d trong đó D là độ dài của đường kính và d là độ dài của dây.
Những quy tắc và công thức trên không chỉ giúp chúng ta hiểu rõ hơn về mối quan hệ giữa đường kính và dây của đường tròn mà còn cung cấp những công cụ quan trọng cho việc tính toán và ứng dụng trong thực tế.
Các ví dụ liên quan
Tính độ dài dây cung:
Cho đường tròn (O; R) và hai điểm A, B bất kỳ trên đường tròn. Biết OA = OB = R. Tính độ dài dây cung AB.
Giải:
Vì OA = OB = R nên O là trung điểm của AB.
⇒ AB = 2 OA = 2R.
Vậy độ dài dây cung AB là 2R.
Tóm lại, lý thuyết về đường kính và dây của đường tròn không chỉ là những khái niệm cơ bản trong hình học mà còn mang lại những ứng dụng to lớn trong thực tế. Việc hiểu và áp dụng chúng không chỉ giúp chúng ta nắm vững hơn về hình dáng và tính chất của đường tròn mà còn mở ra những cánh cửa mới trong sự sáng tạo và ứng dụng.
Đường tròn, với đường kính và dây, không chỉ là một phần của toán học, mà còn là một nguồn cảm hứng không ngừng cho sự hiểu biết và khám phá của chúng ta.