Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật là hai khái niệm quan trọng trong hình học không gian, đặc biệt là với hình hộp chữ nhật. Hiểu rõ hai khái niệm này giúp chúng ta giải quyết các bài toán liên quan đến hình hộp chữ nhật một cách chính xác và hiệu quả.
Diện tích xung quanh của hình hộp chữ nhật
Định nghĩa
Diện tích xung quanh của hình hộp chữ nhật là tổng diện tích bốn mặt bên của hình hộp chữ nhật.
Công thức tính
Để tính diện tích xung quanh của hình hộp chữ nhật ta thực hiện lấy chu vi mặt đáy nhân với chiều cao (cùng đơn vị đo).
Sxq = (a + b) × 2 × h
Với:
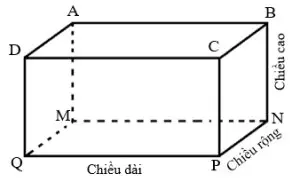
a là chiều dài
b là chiều rộng
h là chiều cao
Chứng minh công thức
Hình hộp chữ nhật có chiều dài a, chiều rộng b, chiều cao h. Có diện tích xung quanh là tổng diện tích 4 mặt bên. Ta có:
Sxq = a x h x 2 + b x h x 2 = (a + b) x 2 x h
Diện tích toàn phần của hình hộp chữ nhật
Định nghĩa
Diện tích toàn phần của hình hộp chữ nhật là tổng của diện tích xung quanh và diện tích hai đáy.
Công thức tính
Để tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.
Stp = Sxq + Sđáy × 2 = (a + b) x 2 x h + 2 x a x b
Với:
a là chiều dài
b là chiều rộng
h là chiều cao
Các dạng bài tập thường gặp và hướng dẫn giải
Dạng 1: Tính diện tích xung quanh hoặc diện tích toàn phần của hình hộp chữ nhật
Phương pháp: Áp dụng công thức tính diện tích xung quanh hoặc diện tích toàn phần.
Ví dụ: Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật có chiều dài 5cm, chiều rộng 7cm và chiều cao 3cm.
Bài giải
Diện tích xung quanh của hình hộp chữ nhật đó là:
Sxq = (5 + 7) x 2 × 3 = 78 (cm2)
Diện tích toàn phần của hình hộp chữ nhật đó là:
Stp = Sxq + Smd x 2 = 78 + (5 x 7) × 2 = 148(cm2)
Đáp số: Diện tích xung quanh: 78cm2 | Diện tích toàn phần: 148cm2
Dạng 2: Biết diện tích xung quanh hoặc diện tích toàn phần, tìm chu vi đáy hoặc chiều cao của hình hộp chữ nhật
Phương pháp:
Từ công thức Sxq = (a + b) x 2 x h:
Tìm chiều cao theo công thức: h = Sxq : [(a + b) x 2] = Sxq: (a + b) : 2;
Tìm tổng chu vi đáy theo công thức: (a + b) x 2 = Sxq : h.
Nếu biết diện tích toàn phần ta cũng thay vào công thức để tìm các đại lượng chưa biết.
Ví dụ. Cho hình hộp chữ nhật có diện tích xung quanh là 217,5m2 và nửa chu vi mặt đáy bằng 14,5m. Tính chiều cao của hình hộp chữ nhật đó.
Bài giải
Chu vi mặt đáy của hình hộp chữ nhật đó là:
14,5 × 2 = 29 (m)
Chiều cao của hình hộp chữ nhật đó là:
217,5 : 29 = 7,5 (m)
Đáp số: 7,5m
Bài tập có lời giải
Bài 1: Một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 3cm, chiều cao 4cm. Tính diện tích xung quanh của hình hộp chữ nhật.
Lời giải:
Diện tích xung quanh của hình hộp chữ nhật là:
Sxq = 2 * (chiều dài + chiều rộng) * chiều cao = 2 * (5cm + 3cm) * 4cm = 32cm²
Vậy, diện tích xung quanh của hình hộp chữ nhật là 32cm².
Bài 2: Một chiếc hộp đựng quà có dạng hình hộp chữ nhật có chiều dài 25cm, chiều rộng 15cm, chiều cao 12cm. Người ta dán giấy kim tuyến lên toàn bộ mặt ngoài của hộp quà. Hỏi diện tích giấy kim tuyến cần dùng là bao nhiêu?
Lời giải:
Diện tích xung quanh của hộp quà là:
Sxq = 2 * (chiều dài + chiều rộng) * chiều cao = 2 * (25cm + 15cm) * 12cm = 960cm²
Diện tích hai mặt đáy của hộp quà là:
2 * diện tích đáy = 2 * (chiều dài * chiều rộng) = 2 * (25cm * 15cm) = 750cm²
Diện tích giấy kim tuyến cần dùng là:
Sxq + 2 * diện tích đáy = 960cm² + 750cm² = 1710cm²
Vậy, diện tích giấy kim tuyến cần dùng là 1710cm².
Bài 3: Một bể cá hình hộp chữ nhật có chiều dài 80cm, chiều rộng 50cm, chiều cao 40cm. Mực nước trong bể cao bằng 3/4 chiều cao của bể. Tính diện tích phần kính cần dùng để làm bể cá (không tính nắp bể).
Lời giải:
Diện tích xung quanh của bể cá là:
Sxq = 2 * (chiều dài + chiều rộng) * chiều cao = 2 * (80cm + 50cm) * 40cm = 5200cm²
Diện tích mặt đáy của bể cá là:
chiều dài * chiều rộng = 80cm * 50cm = 4000cm²
Diện tích phần kính cần dùng để làm bể cá là:
Sxq + 2 * diện tích mặt đáy = 5200cm² + 2 * 4000cm² = 13200cm²
Nắm vững công thức tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật là điều cần thiết cho việc học tập và giải quyết các bài toán thực tế. Bài viết này đã cung cấp cho bạn các công thức tính toán, ví dụ minh họa và bài tập để bạn ôn luyện.
Chúc bạn học tốt với toanhoc.edu.vn
