Diện tích Tam giác đều là một loại tam giác đặc biệt có nhiều ứng dụng trong thực tế. Một trong những tính chất quan trọng của tam giác đều là diện tích. Bài viết này sẽ giới thiệu các phương pháp tính diện tích tam giác đều trong các trường hợp cụ thể và giải một số bài tập ví dụ để minh họa cho các phương pháp tính.
Khái niệm tam giác đều
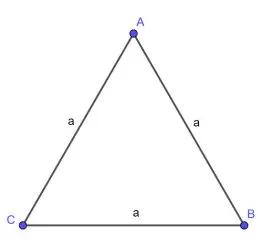
Hình tam giác đều: là tam giác có ba cạnh bằng nhau và ba góc bằng nhau (60°).
Chiều cao: là đoạn thẳng vuông góc kẻ từ đỉnh tam giác đều xuống cạnh đáy.
Công thức tính diện tích tam giác đều
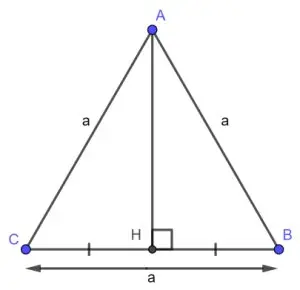
\(S = \frac{(a.h)} { 2}\)
trong đó:
S: Diện tích hình tam giác đều (đơn vị: cm²)
a: Cạnh của hình tam giác đều (đơn vị: cm)
h: Chiều cao của hình tam giác đều (đơn vị: cm)
Chiều cao của hình tam giác đều
Chiều cao của hình tam giác đều được tính bằng công thức:
\[ h = \frac{a \sqrt{3}}{2} \]
Trong đó:
– \( h \) là chiều cao của tam giác đều.
– \( a \) là độ dài cạnh của tam giác đều.
Chứng minh công thức
Cách 1: Sử dụng công thức tính diện tích tam giác và tính chất của tam giác đều.
Cách 2: Chia tam giác đều thành hai tam giác vuông bằng nhau và áp dụng công thức tính diện tích tam giác vuông.
Một số lưu ý khi giải bài tập diện tích tam giác đều cạnh a
Đường cao của tam giác đều được kẻ từ đỉnh A sẽ trùng với đường trung tuyến từ đỉnh đó.
Khi tính diện tích tam giác đều, chiều cao từ góc nào kẻ xuống phải tương ứng với cạnh đáy đó.
Trường hợp có 2 tam giác cùng độ dài chiều cao và chung chiều cao thì diện tích 2 tam giác đó sẽ tỷ lệ thuận với 2 cạnh đáy và ngược lại.
Ngoài công thức tính diện tích tam giác đều như trên đã chia sẻ, các em còn thể vận dụng công thức Heron để tính diện tích tam giác đều:
\(S=a^{2} .\frac{\sqrt{3}}{4}\)
Ví dụ. Cho một tam giác đều ABC, có cạnh AC = AB = BC = 10 cm. Hãy tính diện tích tam giác vuông bằng công thức Heron.
Giải
Ta có: AC = AB = BC = 10 cm
Áp dụng công thức Heron trong tính diện tích tam giác đều ABC, ta có:
\(S=a^{2} .\frac{\sqrt{3}}{4} =10^{2} .\frac{\sqrt{3}}{4} =25\sqrt{3} \left( cm^{2}\right)\)
Vậy, diện tích tam giác đều ABC là \(25\sqrt{3} \left( cm^{2}\right)\)
Bài tập vận dụng
Bài 1. Cho một tam giác đều ABC, có chiều cao là 7cm, và độ dài cạnh đáy là 4cm. Hãy tính diện tích tam giác đều ABC.
Giải
Gọi h là chiều cao được nối từ đỉnh A xuống cạnh BC và a là độ dài cạnh đáy BC.
Theo đề bài ta có: h = 7cm và a = 4cm.
Áp dụng công thức tính diện tích tam giác đều, ta có:
\(S=\frac{1}{2} .a.h=\frac{1}{2} .7.4=14 \left( cm^{2}\right)\)
Vậy diện tích tam giác vuông ABC là \(14 \left( cm^{2}\right)\)
Bài 2. Có một biển quảng cáo hình tam giác đều, có tổng độ dài cạnh đáy và chiều cao là 28m, cạnh đáy lớn hơn chiều cao 12m. Hãy tính diện tích biển quảng cáo hình tam giác đều đó.
Giải
Gọi h là chiều cao của biển quảng cáo hình tam giác đều được nối từ một đỉnh xuống cạnh đáy và a là độ dài cạnh đáy biển quảng cáo này.
Theo đề bài ta có: \(a+h=28m; a=h+12m\)
\(\ a+h=28\)
\(\Leftrightarrow ( h+12) +h=28\)
\(\Leftrightarrow 2h+12=28\)
\(\Leftrightarrow 2h=16\)
\(\Leftrightarrow h=8\)
Vậy chiều cao của biển quảng cáo hình tam giác đều là 8 m. Mà cạnh đáy lại lớn hơn độ cao 12m nên chiều dài cạnh đáy của biển bảng quảng là 20m.
Diện tích biển quảng cáo hình tam giác đều là:
\(S=\frac{1}{2} .a.h=\frac{1}{2} .20.8=80 \left( m^{2}\right)\)
Vậy, diện tích của biển bảng quảng cáo hình tam giác đều là \)80 \left( m^{2}\right)\).
Trên đây là toàn bộ kiến thức về diện tích tam giác đều, cùng một số bài tập vận dụng cơ bản. Hy vọng nó hữu ích và giúp các em học hình học lớp 8 dễ dàng hơn. Có bất kỳ bài tập nào liên quan không giải được, các em hãy để lại bình luận dưới bài viết này, Admin sẽ nhanh chóng hỗ trợ các em.
Chúc bạn học tốt với toanhoc.edu.vn
