Việc tính toán diện tích hình thoi là một kỹ năng quan trọng có nhiều ứng dụng thực tế. Diện tích hình thoi được sử dụng để tính toán diện tích bề mặt, lượng vật liệu cần thiết để chế tạo, và giải các bài toán liên quan đến hình thoi.
Định nghĩa hình thoi
Hình thoi là tứ giác có bốn cạnh bằng nhau và hai đường chéo cắt nhau vuông góc tại trung điểm mỗi đường.
Công thức tính diện tích hình thoi
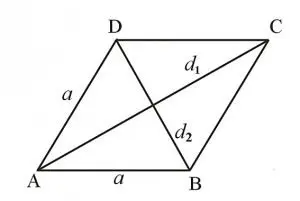
Diện tích hình thoi được tính bằng công thức:
\(S = \frac{1}{2} \times d1 \times d2\)
trong đó:
S: Diện tích hình thoi (đơn vị: cm²)
d1: Độ dài đường chéo thứ nhất (đơn vị: cm)
d2: Độ dài đường chéo thứ hai (đơn vị: cm)
Công thức tính diện tích hình thoi theo cạnh
Diện tích hình thoi cũng có thể được tính bằng công thức:
\(S = a² \times sinα\)
trong đó:
a: Độ dài cạnh hình thoi (đơn vị: cm)
α: Góc giữa hai cạnh kề nhau của hình thoi (đơn vị: độ)
Ví dụ
Cho một hình thoi có độ dài đường chéo thứ nhất là 8cm và độ dài đường chéo thứ hai là 6cm. Hãy tính diện tích hình thoi.
Giải:
Diện tích hình thoi được tính bằng:
\(S = \frac{1}{2} \times d1 \times d2 = \frac{1}{2} \times 8 \times 6 = 24 cm²\)
Các dạng bài tập về diện tích hình thoi
Dạng 1: Tính diện tích hình thoi khi biết độ dài hai đường chéo:
Phương pháp giải:
Áp dụng công thức \(S = \frac{1}{2} \times d1 \times d2\)
Thay giá trị độ dài hai đường chéo vào công thức và tính toán.
Ví dụ:
Cho một hình thoi có độ dài đường chéo thứ nhất là 8cm và độ dài đường chéo thứ hai là 6cm. Hãy tính diện tích hình thoi.
Giải:
Diện tích hình thoi được tính bằng:
\(S = \frac{1}{2} \times d1 \times d2 = \frac{1}{2} \times 8 \times 6 = 24 cm²\)
Dạng 2: Tính diện tích hình thoi khi biết độ dài cạnh và góc giữa hai cạnh kề nhau:
Phương pháp giải:
Áp dụng công thức \(S = a² \times sinα\)
Thay giá trị độ dài cạnh và góc α vào công thức và tính toán.
Ví dụ:
Cho một hình thoi có độ dài cạnh là 5cm và góc giữa hai cạnh kề nhau là 60°. Hãy tính diện tích hình thoi.
Giải:
Diện tích hình thoi được tính bằng:
\(S = a² \times sinα = 5² \times sin 60° = 12.5\sqrt{3}3 cm²\)
Dạng 3: Ứng dụng của diện tích hình thoi:
Phương pháp giải:
Phân tích bài toán để xác định đại lượng cần tính.
Áp dụng các công thức diện tích hình thoi và các kiến thức liên quan để tính toán.
Ví dụ:
Một mảnh đất hình thoi có độ dài đường chéo thứ nhất là 10m và độ dài đường chéo thứ hai là 8m. Người ta muốn trồng cỏ trên mảnh đất này. Hỏi cần mua bao nhiêu mét vuông cỏ?
Giải:
Diện tích mảnh đất hình thoi:
\(S = \frac{1}{2} \times d1 \times d2 = \frac{1}{2} \times 10 \times 8 = 40 m²\)
Diện tích cỏ cần mua:
S = 40 m²
Dạng 4: Bài toán nâng cao:
Phương pháp giải:
Phân tích bài toán để xác định dạng toán.
Áp dụng các kiến thức về hình thoi và các kiến thức toán học khác để giải bài toán.
Ví dụ:
Một hình thoi có diện tích là 30 cm² và độ dài đường chéo thứ nhất là 10cm. Tính độ dài đường chéo thứ hai.
Giải:
Gọi độ dài đường chéo thứ hai là d2.
Diện tích hình thoi:
\(S = \frac{1}{2} \times d1 \times d2 = \frac{1}{2} \times 10 \times d2 = 5d2\)
Thay S = 30 cm² vào phương trình trên, ta được:
5d2 = 30
d2 = 6 cm
Bài tập trắc nghiệm về diện tích hình thoi
Câu 1: Một hình thoi có độ dài đường chéo thứ nhất là 8cm và độ dài đường chéo thứ hai là 6cm. Diện tích hình thoi đó là:
A. 24 cm²
B. 36 cm²
C. 48 cm²
D. 60 cm²
Đáp án: A
Câu 2: Một hình thoi có độ dài cạnh là 5cm và góc giữa hai cạnh kề nhau là 60°. Diện tích hình thoi đó là:
A. 12.5 cm²
B. 25 cm²
C. 37.5 cm²
D. 50 cm²
Đáp án: A
Câu 3: Một mảnh đất hình thoi có độ dài đường chéo thứ nhất là 10m và độ dài đường chéo thứ hai là 8m. Người ta muốn trồng cỏ trên mảnh đất này. Hỏi cần mua bao nhiêu mét vuông cỏ?
A. 40 m²
B. 50 m²
C. 60 m²
D. 70 m²
Đáp án: A
Câu 4: Một hình thoi có diện tích là 30 cm² và độ dài đường chéo thứ nhất là 10cm. Tính độ dài đường chéo thứ hai.
A. 6 cm
B. 8 cm
C. 10 cm
D. 12 cm
Đáp án: A
Câu 5: Một hình thoi có diện tích là 48 cm² và độ dài đường chéo thứ nhất là 12cm. Tính độ dài đường chéo thứ hai.
A. 4 cm
B. 6 cm
C. 8 cm
D. 10 cm
Đáp án: B
Câu 6: Một hình thoi có diện tích là 24 cm² và độ dài đường chéo thứ hai là 8cm. Tính độ dài đường chéo thứ nhất.
A. 3 cm
B. 4 cm
C. 6 cm
D. 8 cm
Đáp án: C
Câu 7: Một hình thoi có độ dài cạnh là 4cm và góc giữa hai cạnh kề nhau là 45°. Diện tích hình thoi đó là:
A. 4 cm²
B. 8 cm²
C. 12 cm²
D. 16 cm²
Đáp án: B
Câu 8: Một hình thoi có độ dài cạnh là 6cm và góc giữa hai cạnh kề nhau là 120°. Diện tích hình thoi đó là:
A. 9 cm²
B. 18 cm²
C. 27 cm²
D. 36 cm²
Đáp án: C
Câu 9: Một hình thoi có độ dài đường chéo thứ nhất là 10cm và độ dài đường chéo thứ hai bằng 3/5 độ dài đường chéo thứ nhất. Diện tích hình thoi đó là:
A. 12 cm²
B. 18 cm²
C. 24 cm²
D. 30 cm²
Đáp án: C
Câu 10: Một hình thoi có độ dài đường chéo thứ nhất là 12cm và độ dài đường chéo thứ hai bằng 2/3 độ dài đường chéo thứ nhất. Diện tích hình thoi đó là:
A. 16 cm²
B. 24 cm²
C. 32 cm²
D. 40 cm²
Đáp án: B
Bài viết này đã hướng dẫn bạn cách tính toán diện tích hình thoi. Bạn đã được học công thức tính diện tích, các ứng dụng của diện tích hình thoi và cách giải một số bài tập liên quan.
Chúc bạn học tốt với toanhoc.edu.vn
