Diện tích hình bình hành là một khái niệm toán học quan trọng giúp tính toán diện tích của các vật có hình bình hành. Bài viết này sẽ hướng dẫn bạn cách tính diện tích hình bình hành
Diện tích hình bình hành là gì?
Diện tích hình bình hành là độ lớn của phần mặt phẳng được giới hạn bởi hình bình hành đó.
Công thức tính diện tích hình bình hành
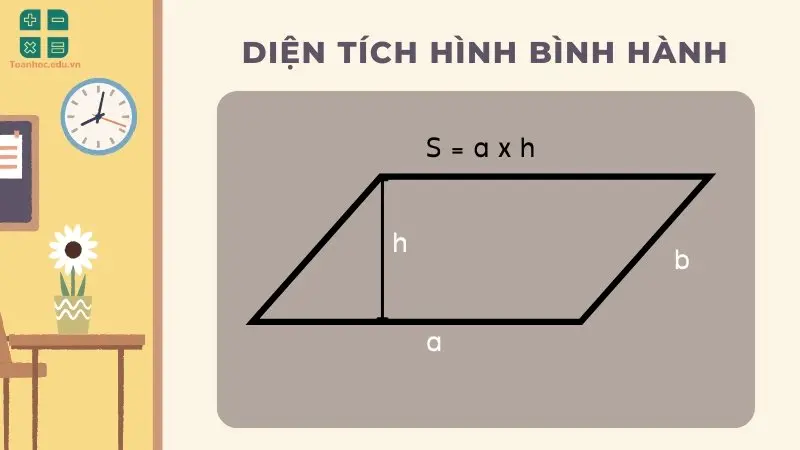
Công thức
$$S = a . h$$
trong đó:
S là diện tích hình bình hành
a là độ dài đáy của hình bình hành
h là chiều cao tương ứng với đáy a
Cách vẽ chiều cao
Từ một đỉnh của hình bình hành, vẽ đường thẳng vuông góc với cạnh đối diện.
Đoạn thẳng vuông góc đó chính là chiều cao của hình bình hành.
Ví dụ:
Một hình bình hành có độ dài đáy là 8cm và chiều cao tương ứng là 5cm. Diện tích hình bình hành đó là:
S = 8 x 5 = 40 (cm²)
Đơn vị đo diện tích
Đơn vị đo diện tích thường dùng là:
Xăng-ti-mét vuông (cm²)
Mét vuông (m²)
Đề-ca-mét vuông (dam²)
Héc-ta (ha)
Cách tính diện tích hình bình hành khi biết hai đường chéo
Thông thường nếu đề bài chỉ cho một dữ kiện về độ dài của hai đường chéo không thôi thì chắc chắc chúng ta không giải được. Vì thế, đề sẽ thường cho yếu tố góc giữa hai đường chéo đi kèm. Cụ thể như sau:
Cho hình bình hành ABCD có AC và BD là hai đường chéo, giao điểm của hai đường chéo là O và số đo góc AOB tạo bởi hai đường chéo. Diện tích hình bình hành khi biết độ dài hai đường chéo được tính như sau:
$$S = \frac{1}{2} \cdot AC \cdot BD \cdot \sin(\angle AOB) = \frac{1}{2} \cdot AC \cdot BD \cdot \sin(\angle AOD)$$
Công thức tổng quát tính diện tích hình bình hành khi biết hai đường chéo là: S = 1/2.c.d.sinα
Với:
c, d lần lượt là độ dài của hai đường chéo hình bình hành (cùng đơn vị đo)
α là góc tạo bởi hai đường chéo.
Các dạng bài tập về diện tích hình bình hành
Dạng 1: Tính diện tích hình bình hành khi biết độ dài đáy và chiều cao.
Ví dụ:
Một hình bình hành có độ dài đáy là 8cm và chiều cao là 5cm. Diện tích hình bình hành đó là:
S = 8 x 5 = 40 (cm²)
Dạng 2: Tìm độ dài đáy hoặc chiều cao khi biết diện tích và một trong hai đại lượng kia.
Ví dụ: Một hình bình hành có diện tích là 30cm² và chiều cao là 5cm. Tìm độ dài đáy của hình bình hành đó.
Giải:
Đáy = \(\frac{Diện tích}{Chiều cao} = \frac{30}{5}\) = 6 (cm)
Dạng 3: So sánh diện tích hai hình bình hành.
Ví dụ: So sánh diện tích hai hình bình hành có độ dài đáy lần lượt là 5cm và 7cm, chiều cao cùng là 4cm.
Giải:
Diện tích hình bình hành 1 = 5 x 4 = 20 (cm²)
Diện tích hình bình hành 2 = 7 x 4 = 28 (cm²)
Diện tích hình bình hành 2 > Diện tích hình bình hành 1 (28 cm² > 20 cm²)
Dạng 4: Vẽ hình bình hành theo diện tích và một trong hai đại lượng: đáy hoặc chiều cao.
Ví dụ: Vẽ hình bình hành có diện tích là 24cm² và độ dài đáy là 6cm.
Giải:
Chiều cao = \(\frac{Diện tích}{Đáy} = \frac{24}{6}\) = 4 (cm)
Vẽ hình chữ nhật có chiều dài 6cm và chiều rộng 4cm.
Bài tập sách giáo khoa Toán lớp 4
Sách giáo khoa Toán lớp 4 tập 2, trang 104:
Bài 1:
Tính diện tích mỗi hình bình hành sau:
Bài 2:
Viết tiếp vào ô trống:
a) Diện tích hình bình hành ABCD bằng …
b) Diện tích hình bình hành MNPQ bằng …
Bài 3:
Vẽ hình bình hành theo yêu cầu:
a) Vẽ hình bình hành ABCD có AB = 5cm, BC = 4cm.
b) Vẽ hình bình hành MNPQ có MN = 7cm, MQ = 6cm.
Gợi ý giải bài tập:
Bài 1:
Diện tích hình bình hành = Độ dài đáy x Chiều cao
Ví dụ:
a) Diện tích hình bình hành = 8 x 5 = 40 (cm²)
Bài 2:
a) Diện tích hình bình hành ABCD = a x h
b) Diện tích hình bình hành MNPQ = MN x PQ
Bài 3:
Vẽ hai đường thẳng song song và cách nhau một khoảng bằng độ dài cạnh đáy. Nối hai đầu mút của hai đường thẳng đó bằng hai đoạn thẳng có độ dài bằng nhau.
Hãy áp dụng kiến thức này để giải các bài toán liên quan đến diện tích hình bình hành
Chúc bạn học tốt với toanhoc.edu.vn
