Dấu hiệu nhận biết tiếp tuyến của đường tròn - Toán lớp 9

Trong hình học, việc nhận biết tiếp tuyến của đường tròn là một kỹ năng quan trọng, giúp chúng ta xác định vị trí của các đường thẳng tiếp xúc với đường tròn tại một điểm duy nhất trên bề mặt của nó.

Dấu hiệu nhận biết này cung cấp các phương pháp và quy tắc để xác định xem một đường thẳng có tiếp xúc với đường tròn và tạo thành tiếp tuyến hay không. Hãy cùng khám phá về các dấu hiệu nhận biết tiếp tuyến của đường tròn trong bài viết dưới đây.

Định nghĩa

Tiếp tuyến:là đường thẳng đi qua một điểm trên đường tròn và vuông góc với bán kính đi qua điểm đó.

Bán kính:là đoạn thẳng nối tâm đường tròn với một điểm trên đường tròn.

Tâm đường tròn:là điểm nằm chính giữa đường tròn.

Dấu hiệu nhận biết

Nếu một đường thẳng và một đường tròn chỉ có một điểm chung thì đường thẳng đó là tiếp tuyến của đường tròn.

Giải thích:

Khi đường thẳng và đường tròn chỉ có một điểm chung, ta có thể tưởng tượng điểm chung đó như là “điểm tiếp xúc” giữa đường thẳng và đường tròn.

Do “điểm tiếp xúc” là điểm nằm trên đường tròn, nên đường thẳng đi qua điểm này sẽ vuông góc với bán kính đi qua điểm đó để đảm bảo “tiếp xúc” mà không “cắt” vào đường tròn.

Ví dụ:

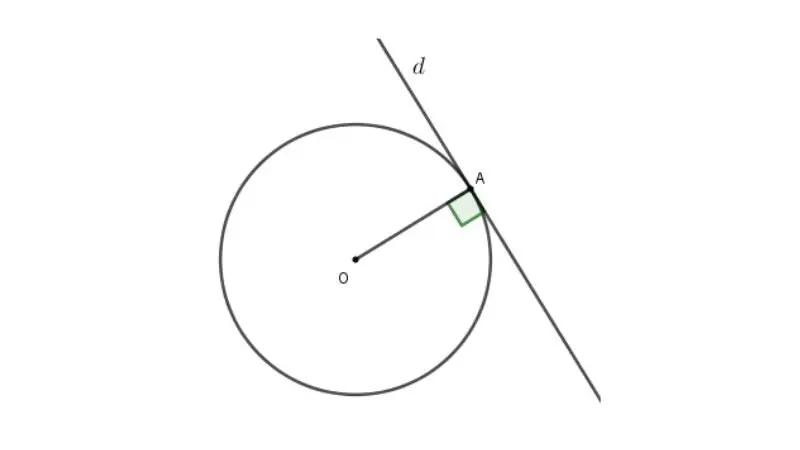
Cho đường tròn (O; R) và đường thẳng d đi qua A thuộc đường tròn và không đi qua tâm O.

Khi đó, d là tiếp tuyến của đường tròn (O; R) tại A.

Nếu một đường thẳng đi qua một điểm trên đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng đó là tiếp tuyến của đường tròn.

Giải thích:

• Khi đường thẳng vuông góc với bán kính, ta có thể đảm bảo rằng đường thẳng này chỉ có một điểm chung với đường tròn, đó là điểm “tiếp xúc”.
• Do đó, đường thẳng này thỏa mãn định nghĩa của tiếp tuyến.

Ví dụ:

• Cho đường tròn (O; R) và điểm A trên đường tròn.
• Vẽ đường thẳng d vuông góc với OA tại A.
• Khi đó, d là tiếp tuyến của đường tròn (O; R) tại A.

Khoảng cách từ tâm đến điểm tiếp xúc

Khoảng cách từ tâm của đường tròn đến điểm tiếp xúc trên đường tròn là một dấu hiệu quan trọng để nhận biết tiếp tuyến của đường tròn. Đặc điểm này có ý nghĩa quan trọng trong hình học và được sử dụng rộng rãi trong việc giải các bài toán liên quan đến đường tròn.

Khoảng cách này bằng bán kính của đường tròn. Điều này xuất phát từ tính chất của tiếp tuyến là đường thẳng vuông góc với bán kính tại điểm tiếp xúc. Do đó, nếu một đường thẳng tiếp xúc với đường tròn tại một điểm, thì khoảng cách từ tâm của đường tròn đến điểm tiếp xúc sẽ bằng bán kính của đường tròn.

Công thức tính khoảng cách từ tâm của đường tròn đến điểm tiếp xúc có thể được biểu diễn như sau:d=r

Trong đó:

dlà khoảng cách từ tâm của đường tròn đến điểm tiếp xúc.

rlà bán kính của đường tròn.

Công thức này cung cấp một cách tiếp cận đơn giản và hiệu quả để xác định vị trí của điểm tiếp xúc và ứng dụng trong việc giải các bài toán liên quan đến đường tròn.

Ví dụ 1:Cho đường tròn (O; R) và điểm M nằm ngoài đường tròn. Vẽ hai tiếp tuyến MA và MB từ M đến đường tròn.

Giải:

• OA = OB = R (theo định nghĩa)
• MA = MB (theo hệ quả)

Phương trình tiếp tuyến 

Phương trình tiếp tuyến của đường tròn là phương trình biểu thị mối liên hệ giữa hai tọa độ x và y của một điểm trên đường tiếp tuyến.

Các dạng phương trình tiếp tuyến:

Dạng 1:

Phương trình tiếp tuyến của đường tròn (O; R) tại điểm M(x0; y0) có dạng:

a(x – x0) + b(y – y0) = 0

với a và b là các hệ số thỏa mãn điều kiện:

\(a^2 + b^2 \neq 0\)
\(axO + byO – R^2 = 0\)
Dạng 2:

Phương trình tiếp tuyến của đường tròn (O; R) có dạng:

y = mx + n

với m và n là các hệ số thỏa mãn điều kiện:

\(m^2 + 1 \neq 0\)
\(d(O; d) = R\)

với d là đường thẳng có phương trình y = mx + n.

Cách xác định hệ số:

Cách 1:Sử dụng định nghĩa tiếp tuyến.

• Bước 1:Tìm tọa độ điểm M là điểm tiếp xúc của đường tiếp tuyến và đường tròn.
• Bước 2:Viết phương trình đường thẳng đi qua điểm M và vuông góc với bán kính OM.

Cách 2:Sử dụng công thức.

• Bước 1:Tìm tọa độ điểm M là điểm tiếp xúc của đường tiếp tuyến và đường tròn.
• Bước 2:Thay tọa độ điểm M vào các điều kiện để tìm a và b (dạng 1) hoặc m và n (dạng 2).

Ví dụ :Cho đường tròn (O; 5) và điểm M(3; 4). Viết phương trình tiếp tuyến của đường tròn tại M.

Giải:

Cách 1:

Tìm tọa độ điểm M là điểm tiếp xúc của đường tiếp tuyến và đường tròn.

Viết phương trình đường thẳng đi qua điểm M và vuông góc với bán kính OM.

Cách 2:

Tìm tọa độ điểm M là điểm tiếp xúc của đường tiếp tuyến và đường tròn.

Thay tọa độ điểm M vào các điều kiện để tìm a và b.

Góc giữa đường thẳng và bán kính

Góc giữa đường thẳng và bán kính là góc tạo bởi đường thẳng và bán kính đi qua điểm chung của đường thẳng và đường tròn.

Cách xác định:

Cách 1:Sử dụng thước đo góc.

• Vẽ đường thẳng và bán kính.
• Đặt thước đo góc vào điểm chung của đường thẳng và bán kính.
• Đo góc tạo bởi đường thẳng và bán kính.

Cách 2:Sử dụng công thức lượng giác.

• Tìm tọa độ điểm chung của đường thẳng và đường tròn.
• Sử dụng công thức lượng giác để tính góc tạo bởi hai vectơ: vectơ chỉ phương của đường thẳng và vectơ chỉ hướng của bán kính.

Ví dụ:Cho đường tròn (O; 5) và đường thẳng d: y = 2x + 1. Tìm góc giữa đường thẳng d và bán kính đi qua điểm chung của d và đường tròn.

Giải:

• Bước 1:Tìm điểm M là điểm chung của đường tròn và đường thẳng.
• Bước 2:Vẽ bán kính OM.
• Bước 3:Sử dụng thước đo góc hoặc công thức lượng giác để tính góc tạo bởi d và OM.

Hệ quả

Một hệ quả quan trọng của việc nhận biết tiếp tuyến của đường tròn là khả năng xác định vị trí của đường thẳng tiếp tuyến và điểm tiếp xúc trên đường tròn. Bằng cách này, chúng ta có thể:

Xây dựng phương trình tiếp tuyến: Khi biết tọa độ của điểm tiếp xúc trên đường tròn, chúng ta có thể dễ dàng xây dựng được phương trình của đường thẳng tiếp tuyến. Điều này cung cấp một cách tiếp cận hiệu quả để tính toán và phân tích các vấn đề liên quan đến đường tròn.

Tính toán các thông số liên quan: Bằng cách xác định vị trí của điểm tiếp xúc và phương trình của đường thẳng tiếp tuyến, chúng ta có thể tính toán các thông số khác như góc, khoảng cách và các tương tác khác giữa đường thẳng và đường tròn.

Ứng dụng trong thực tế: Hiểu biết về việc nhận biết tiếp tuyến của đường tròn là quan trọng trong nhiều lĩnh vực thực tế như kỹ thuật, thiết kế và xây dựng. Việc có thể xác định vị trí của đường thẳng tiếp tuyến là một phần quan trọng của quá trình thiết kế và tính toán.

Giải quyết các bài toán hình học: Các dấu hiệu nhận biết tiếp tuyến của đường tròn là công cụ hữu ích trong việc giải quyết các bài toán hình học liên quan đến đường tròn. Chúng giúp chúng ta hiểu sâu hơn về tính chất và mối quan hệ giữa các thành phần hình học.

Tóm lại, việc hiểu và áp dụng các dấu hiệu nhận biết tiếp tuyến của đường tròn là một kỹ năng quan trọng trong hình học, giúp chúng ta xác định vị trí của các đường thẳng tiếp xúc với đường tròn. Bằng cách sử dụng các quy tắc và phương pháp được đề cập trong bài viết, chúng ta có thể dễ dàng xác định xem một đường thẳng có tiếp xúc với đường tròn và tạo thành tiếp tuyến hay không.

Việc áp dụng những kiến thức này không chỉ giúp chúng ta hiểu sâu hơn về tính chất của đường tròn mà còn làm nền tảng cho việc giải các bài toán và ứng dụng trong thực tế.