Hệ thống kiến thức đầy đủ về đạo hàm của hàm số lượng giác

Hệ thống kiến thức đầy đủ về đạo hàm của hàm số lượng giác

Hàm số lượng giác đóng vai trò quan trọng trong nhiều lĩnh vực của toán học và khoa học.

Đạo hàm của hàm số lượng giác là một khái niệm quan trọng trong Giải tích 11, giúp chúng ta nghiên cứu sự thay đổi của hàm số lượng giác theo biến số.Bài viết này sẽ cung cấp cho bạn kiến thức về đạo hàm của các hàm số lượng giác cơ bản

Đạo hàm của hàm số lượng giác là gì?

Đạo hàm của hàm lượng giác là phương pháp toán học tìm tốc độ biến thiên của một hàm số lượng giác theo sự biến thiên của biển số. Một số hàm số lượng giác thường gặp nhất đó là hàm: sin(x), cos(x) và tan(x).

Đạo hàm sơ cấp, đạo hàm thứ cấp

Đạo hàm của hàm số sơ cấp cơ bản

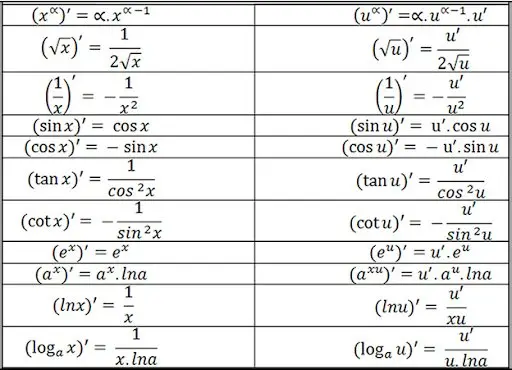
Đạo hàm của hàm số lượng giác ngược

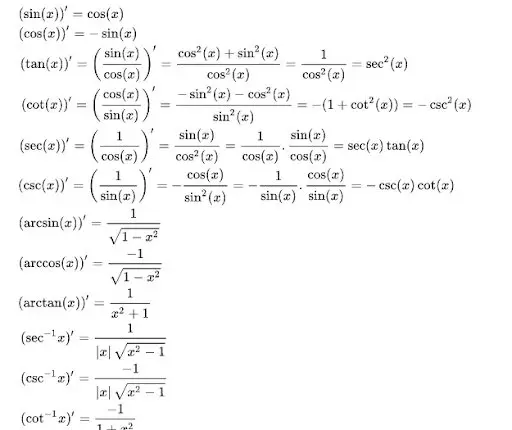
Cách giải bài tập về đạo hàm của hàm số lượng giác

Bước 1: Xác định hàm số cần tính đạo hàm.

Bước 2: Chọn công thức đạo hàm phù hợp.

Bước 3: Áp dụng công thức đạo hàm đã chọn vào hàm số cần tính đạo hàm.

Bước 4: Kiểm tra lại kết quả.

Ví dụ:

Tính đạo hàm của hàm số \(f(x) = sin(x) + cos(x)\)

Lời giải:

Bước 1: Hàm số cần tính đạo hàm là \(f(x) = sin(x) + cos(x)\)

Bước 2: Chọn công thức đạo hàm phù hợp:

• \((sin(x))’ = cos(x)\)
• \((cos(x))’ = -sin(x)\)

Bước 3: Áp dụng công thức đạo hàm đã chọn:

\(f'(x) = (sin(x))’ + (cos(x))’\)

= \(cos(x) – sin(x)\)

Bước 4: Kiểm tra lại kết quả:

Đạo hàm của \(f(x) = sin(x) + cos(x)\) là \(f'(x) = cos(x) – sin(x)\)

Bài tập đạo hàm của hàm số lượng giác có lời giải chi tiết

Bài 1:

\[
\text{Tính đạo hàm của hàm số sau:}
\]

\[
y = \sin 2x \cdot \cos^4 x – \cot \frac{1}{x^2} – \sin^2 x \cdot \sin \frac{1}{x}
\]

\[
\text{Bài giải:}
\]

\[
y = \sin 2x \cdot \cos^4 x – \cot \frac{1}{x^2} – \sin^2 x \cdot \sin \frac{1}{x}
\]

\[
\( \sin 2x \cdot (\cos^4 x – \sin^4 x) – \cot \frac{1}{x^2}\)
\]

\[
\text{Do đó:}
\]

\[
y’ = \frac{1}{4} \cdot 2\cos 4x + \frac{1}{\sin^2 \frac{1}{x^2}} \cdot \left( -\frac{1}{x^2} \right)’ = 2\cos 4x – \frac{2}{x^3 \sin^2 \frac{1}{x^2}}
\]

Bài 2:

\[
\text{Tính đạo hàm của hàm số sau:}
\]

\[
y = \tan(2x + 1) – x^2\cos^2x
\]

\[
\text{Bài giải:}
\]

\[
y’ = \frac{2}{\cos^2(2x + 1)} – (x^2)’ \cdot \cos^2x – x^2 \cdot (\cos^2x)’
\]

\[
= \frac{2}{\cos^2(2x + 1)} – 2x \cdot \cos^2x – x^2 \cdot (-2\sin x \cdot \cos x)
\]

\[
= \frac{2}{\cos^2(2x + 1)} – 2x \cdot \cos^2x + 2x^2 \cdot \sin 2x
\]

Bài 3:

\[
\text{Tìm biểu thức đạo hàm của hàm số sau:}
\]

\[
f(t) = \frac{t + \tan t}{t – 1}
\]

\[
\text{Bài giải:}
\]

\[
f'(t) = \left( \frac{1 + \tan^2 t}{(t – 1)^2} \right)(t – 1) – \frac{t + \tan t}{(t – 1)^2}(\tan^2 t + 1) – \frac{t + \tan t}{(t – 1)^2}
\]

\[
= \frac{(1 + \tan^2 t)(t – 1) – (t + \tan t)(\tan^2 t + 1) – t – \tan t}{(t – 1)^2}
\]

Luyện tập đạo hàm của hàm số lượng giác

Câu 1: Tính đạo hàm của các hàm số sau:

1. a) \(f(x) = sin(2x) + cos(3x)\)
2. b) \(g(x) = tan(x) + cot(x)\)
3. c) \(h(x) = sec(x) + csc(x)\)

Câu 2: Tìm đạo hàm của hàm số \(f(x) = sin^2(x) + cos^2(x)\)

Câu 3: Cho hàm số \(f(x) = sin(x) + cos(x)\). Chứng minh rằng \(f'(x) = cos(x) – sin(x)\)

Câu 4: Giải phương trình \(f'(x) = 0\), với f(x) là hàm số được cho trong câu 1.

Câu 5: Vẽ đồ thị của hàm số \(f(x) = sin(x)\) và f'(x) trên cùng một hệ trục tọa độ.

Hy vọng bài viết này đã cung cấp cho bạn kiến thức đầy đủ về đạo hàm của các hàm số lượng giác cơ bản về Đạo hàm của các hàm số lượng giác cơ bản (sin, cos, tan, cot) đã được học trong chương trình Toán lớp 11.