Thể tích khối chóp tứ giác đều là một hình khối quen thuộc trong toán học và có nhiều ứng dụng trong thực tế. Hiểu về thể tích của khối chóp tứ giác đều là điều cần thiết để giải quyết các bài toán liên quan đến hình khối này.
Khái niệm khối chóp tứ giác đều
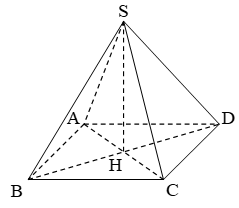
Khối chóp tứ giác đều là hình khối được tạo thành bởi việc nối các đỉnh của một tứ giác đều với một điểm chung S không nằm trên mặt phẳng của tứ giác.
Mặt đáy là tứ giác đều.
Chiều cao là khoảng cách từ đỉnh S đến mặt phẳng đáy.
Công thức tính thể tích khối chóp tứ giác đều
\(V = (\frac{1}{3}) * S_{đáy} * h\)trong đó:
V là thể tích của khối chóp.
\(S_{đáy}\) là diện tích của mặt đáy.
h là chiều cao.
Diện tích mặt đáy
\(S_{đáy} = \frac{a²}{sqrt{3}}\)trong đó:
a là độ dài cạnh của tứ giác đều.
Công thức tính thể tích khối chóp tứ giác đều theo cạnh a
\(V =\frac{a^3\sqrt{3}}{12}\)Ví dụ:
Cho một khối chóp tứ giác đều có cạnh đáy a = 5cm và chiều cao h = 10cm. Thể tích của khối chóp là:
\(V =\frac{1}{3} \times S_{\text{đáy}} \times h = \frac{1}{3} \times (5^2\sqrt{3}) \times 10 = 125\sqrt{3} \text{ cm}^3\)Các dạng bài tập về thể tích khối chóp tứ giác đều
Dạng 1: Cho cạnh đáy và chiều cao, tính thể tích khối chóp.
Phương pháp giải:
Áp dụng công thức \( V = (\frac{1}{3}) * S_{đáy} * h\)
Tính \(S_{đáy} = a²\sqrt{3}\).
Thay \(S_{đáy}\) và h vào công thức để tính V.
Ví dụ: Cho một khối chóp tứ giác đều có cạnh đáy a = 5cm và chiều cao h = 10cm. Tính thể tích của khối chóp.
Giải:
\(S_{đáy} = a^2\sqrt{3} = 5^2\sqrt{3} = 25\sqrt{3} cm²\).
\(V = \frac{1}{3} \times S_{\text{đáy}} \times h = \frac{1}{3} \times 25\sqrt{3} \times 10 = 125\sqrt{3} \text{ cm}^3\)Dạng 2: Cho diện tích đáy và chiều cao, tính thể tích khối chóp.
Phương pháp giải:
Thay \(S_{đáy} vào công thức V = (\frac{1}{3}) * S_{đáy} * h\) để tính V.
Ví dụ: Cho một khối chóp tứ giác đều có diện tích đáy \(S_{đáy} = 50cm²\) và chiều cao h = 10cm. Tính thể tích của khối chóp.
Giải:
\(V = (\frac{1}{3}) * S_{đáy} * h = (\frac{1}{3}) * 50 * 10 = 166,67 cm³\).
Dạng 3: Cho thể tích và chiều cao, tính cạnh đáy.
Phương pháp giải:
Thay V và h vào công thức \(V = (\frac{1}{3}) * S_{đáy} * h \text{để tính} S_{đáy}\)
Giải phương trình \(S_{đáy} = a²\sqrt{3}\) để tìm a.
Ví dụ: Cho một khối chóp tứ giác đều có thể tích \(V = 125\sqrt{3} cm³\) và chiều cao h = 10cm. Tính cạnh đáy của khối chóp.
Giải:
\(V = (\frac{1}{3}) * S_{đáy} * h => S_{đáy} = 3V/(h) = 3 * 125\sqrt{3} / 10 = 37,5\sqrt{3} cm²\).
\(S_{\text{đáy}} = a^2\sqrt{3} \Rightarrow a = \sqrt{\frac{S_{\text{đáy}}}{\sqrt{3}}} = \sqrt{\frac{37.5\sqrt{3}}{\sqrt{3}}} = 5 \text{ cm}\)Dạng 4: Cho các yếu tố khác (như đường chéo của hình vuông tạo thành mặt đáy), tính thể tích.
Phương pháp giải:
Sử dụng các mối quan hệ hình học để tính các đại lượng cần thiết (a, h).
Thay các giá trị vào công thức \(V = \left(\frac{1}{3}\right) \times S_{\text{đáy}} \times h\) để tính V.
Ví dụ: Cho một khối chóp tứ giác đều được tạo thành bởi việc quay một hình vuông có cạnh a = 6cm xung quanh một trục. Tính thể tích của khối chóp.
Giải:
Đường chéo của hình vuông: \(d = a\sqrt{2} = 6\sqrt{2}\) cm.
Chiều cao của khối chóp: \(h = \frac{d}{2} = 3\sqrt{2}\)cm.
Diện tích đáy: \(S_{đáy} = a² = 6² = 36 cm²\).
Thể tích của khối chóp: \(V = (\frac{1}{3}) * S_{đáy} * h = (\frac{1}{3}) * 36 * 3\sqrt{2} = 36\sqrt{2} cm³\).
Bài tập về thể tích khối chóp tứ giác đều có lời giải
Bài 1: Cho một khối chóp tứ giác đều có cạnh đáy a = 5cm và chiều cao h = 10cm. Tính thể tích của khối chóp.
Giải:
\(S_{\text{đáy}} = a^2\sqrt{3} = 5^2\sqrt{3} = 25\sqrt{3} \text{ cm}^2\)\(V = \left(\frac{1}{3}\right) \times S_{\text{đáy}} \times h = \left(\frac{1}{3}\right) \times 25\sqrt{3} \times 10 = 125\sqrt{3} \text{ cm}^3\).
Bài 2: Cho một khối chóp tứ giác đều có diện tích đáy \(S_{đáy}\) = 50cm² và chiều cao h = 10cm. Tính thể tích của khối chóp.
Giải:
\(V = (\frac{1}{3}) * S_{đáy} * h = (\frac{1}{3}) * 50 * 10 = 166,67 cm³V = \left(\frac{1}{3}\right) \cdot S_{đáy} \cdot h \Rightarrow S_{đáy} = \frac{3V}{h} = \frac{3 \cdot 125\sqrt{3}}{10} = 37.5\sqrt{3} \, \text{cm}^2\)
.
Bài 3: Cho một khối chóp tứ giác đều có thể tích \(V = 125\sqrt{3}\) cm³ và chiều cao h = 10cm. Tính cạnh đáy của khối chóp.
Giải:
\(V = \left(\frac{1}{3}\right) \cdot S_{đáy} \cdot h \Rightarrow S_{đáy} = \frac{3V}{h} = \frac{3 \cdot 125\sqrt{3}}{10} = 37.5\sqrt{3} \, \text{cm}^2\).
\(S_{đáy} = a^2\sqrt{3} \Rightarrow a = \sqrt{\frac{S_{đáy}}{\sqrt{3}}} = \sqrt{\frac{37.5\sqrt{3}}{\sqrt{3}}} = 5 \, \text{cm}\).
Bài 4: Cho một khối chóp tứ giác đều được tạo thành bởi việc quay một hình vuông có cạnh a = 6cm xung quanh một trục. Tính thể tích của khối chóp.
Giải:
Đường chéo của hình vuông: \(d = a\sqrt{2} = 6\sqrt{2} \text{ cm}\)
Chiều cao của khối chóp: \(h = \frac{d}{2} = \frac{3\sqrt{2}}{2} \text{ cm}\)
Diện tích đáy: \(S_{đáy} = a² = 6² = 36 cm²\).
Thể tích của khối chóp: \(V = \left(\frac{1}{3}\right) \times S_{\text{đáy}} \times h = \left(\frac{1}{3}\right) \times 36 \times 3\sqrt{2} = 36\sqrt{2} \text{ cm}^3\)
Bài 5: Một kim tự tháp hình chóp tứ giác đều có cạnh đáy a = 10m và chiều cao h = 20m. Thể tích của kim tự tháp là:
Giải:
\(S_{đáy} = \frac{a²}{sqrt{3}} = \frac{10²}{sqrt{3}} = \frac{100}{sqrt{3}} m²\).
\(V = (\frac{1}{3}) * S_{đáy} * h = (\frac{1}{3}) * \frac{100}{sqrt{3}} * 20 = 666,67 m³\).
Thể tích khối chóp tứ giác đều là một khái niệm quan trọng trong toán học và có nhiều ứng dụng trong thực tế. Việc nắm vững công thức tính thể tích và phương pháp giải các bài toán liên quan đến khối chóp tứ giác đều là điều cần thiết cho học sinh, sinh viên và những người làm việc trong lĩnh vực kỹ thuật.
Chúc bạn học tốt với toanhoc.edu.vn








