Tập hợp Q là một trong những khái niệm quan trọng trong chương trình Toán lớp 7.Bài viết này sẽ cung cấp cho bạn kiến thức về tập hợp Q, bao gồm định nghĩa, tính chất, cách biểu diễn số hữu tỉ trên trục số, so sánh hai số hữu tỉ, và một số ứng dụng cơ bản.
Định nghĩa tập hợp Q các số hữu tỉ
Số hữu tỉ là số có thể viết dưới dạng phân số a/b với a, b là số nguyên và b ≠ 0.
Tập hợp Q là tập hợp tất cả các số hữu tỉ.
Biểu diễn số hữu tỉ trên trục số
Mỗi số hữu tỉ được biểu diễn bởi một điểm trên trục số.
Cách biểu diễn:
Chọn điểm O trên trục số.
Đánh dấu các điểm 1, 2, 3, … về bên phải O.
Đánh dấu các điểm -1, -2, -3, … về bên trái O.
Mỗi phân số a/b được biểu diễn bởi điểm M sao cho OM chia đoạn thẳng OA thành a phần bằng nhau và b phần như vậy.
So sánh hai số hữu tỉ
Quy tắc
Nếu a < b thì \(\frac{a}{b} < 0 \)
Nếu a = b thì \(\frac{a}{b} = 0 \)
Nếu a = b thì \(\frac{a}{b} > 0 \)
Cách so sánh
Viết hai số hữu tỉ về dạng phân số có cùng mẫu dương.
So sánh hai tử số.
Tính chất
Tính chất giao hoán
\(\frac{a}{b} + \frac{c}{d} = \frac{c}{d} + \frac{a}{b} \)
Tính chất kết hợp
\(\frac{a}{b} + \left( \frac{c}{d} + \frac{e}{f} \right) = \left( \frac{a}{b} + \frac{c}{d} \right) + \frac{e}{f} \)
Tính chất phân phối
\(\frac{a}{b} \cdot \left( \frac{c}{d} + \frac{e}{f} \right) = \frac{a}{b} \cdot \frac{c}{d} + \frac{a}{b} \cdot \frac{e}{f}\)
Biểu diễn tập hợp Q các số hữu tỉ trên trục số
Cách biểu diễn số hữu tỉ a/b ( a và b thuộc Z, b khác 0) trên trục số:
Bước 1: Chia đoạn đơn vị [0; 1] trên trục số thành b phần bằng nhau. Ta có một phần là 1/b là đơn vị mới.
Bước 2: Xét trường hợp:
a > 0 thì điểm biểu diễn a/b nằm bên phải 0, cách 0 một khoảng a lần đơn vị mới.
a< 0 thì điểm biểu diễn a/b nằm bên trái 0, cách 0 một khoảng |a| lần đơn vị mới.
Điểm biểu diễn a/b được gọi là điểm a/b.
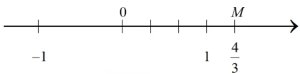
Ví dụ: Biểu diễn 4/3 trên trục số:
Bước 1: Ta chia trục số thành 3 phần bằng nhau. Chọn 1 đoạn làm đơn vị mới bằng 1/3 đơn vị cũ.
Bước 2: Ta biểu diễn số hữu tỉ 4/3 bằng điểm M. Biết 4 > 0 => M nằm bên phải trục số và cách điểm 0 một khoảng bằng 4 đơn vị
Bài tập tự luyện có lời giải chi tiết
Bài 1: Cho các số hữu tỉ sau: 1/2 , 0 , -5/3, 4/5, -8/4 , 78/99, 12/100, -5/6
a) Số nào là số hữu tỉ âm?
b) Số nào là số hữu tỉ dương?
c) Số nào không là số hữu tỉ âm, không là số hữu tỉ dương?
Lời giải:
a) Số hữu tỉ âm là: \(\frac{-5}{3}, \frac{-8}{4}, \frac{-5}{6}\)
b) Số hữu tỉ dương là: \(\frac{1}{2}, \frac{4}{5}, \frac{78}{99}, \frac{12}{100}\)
c) 0 không là số hữu tỉ âm, không là số hữu tỉ dương.
Bài 2: Giải thích lí do các số: \(\frac{6,5}{2}, \frac{-3}{8}, \frac{2}{7}\) là các số hữu tỉ.
Lời giải:
Các số 6, 5/2, -3/8, 2/7 là số hữu tỉ vì có thể biêu diễn dưới dạng phân số a/b ( a và b thuộc Z, b khác 0).
\(6 = \frac{12}{2} = \frac{18}{3}= \frac{24}{4}\) =…
\(\frac{5}{2} = \frac{10}{4} = \frac{15}{6} = \frac{25}{10}\) = …
\(\frac{-3}{8} = \frac{-6}{18} = \frac{-12}{32} = \frac{-15}{40}\) = …
\(\frac{2}{7} = \frac{4}{14} = \frac{6}{21} = \frac{8}{28}\) = …
Bài tập tự luyện
Viết các số sau đây dưới dạng phân số tối giản:
a) 0,375; b) -1,125; c) 1,875; d) -2,75.
So sánh hai số hữu tỉ sau:
a) \(\frac{3}{5} và \frac{7}{11}\);
b)\( \frac{-2}{3} và \frac{-5}{7}\)
Giải bài toán:
Một xe đạp đi từ A đến B với vận tốc 12 km/h. Sau 2 giờ, một xe máy đi từ B về A với vận tốc 30 km/h. Hỏi sau bao lâu hai xe gặp nhau?
a) Một mảnh vườn hình chữ nhật có chiều dài 20m, chiều rộng bằng 53 chiều dài. Tính diện tích mảnh vườn.
b) Một bể nước có dung tích 1500 lít. Người ta đã đổ vào bể 750 lít nước. Hỏi cần phải đổ thêm bao nhiêu lít nước nữa để đầy bể?
Hiểu rõ về tập hợp Q là nền tảng để giải quyết nhiều dạng bài tập toán học và ứng dụng thực tế. Bài viết này đã cung cấp cho bạn kiến thức cơ bản về tập hợp Q.








