Tam giác cân là một trong những khái niệm cơ bản và quan trọng nhất trong môn Toán học lớp 7. Nó là nền tảng cho nhiều định lý, tính chất và bài toán liên quan đến tam giác.
Định nghĩa tam giác cân
Tam giác cân là tam giác có hai cạnh bằng nhau. Hai cạnh bằng nhau được gọi là hai cạnh bên. Cạnh còn lại là cạnh đáy.
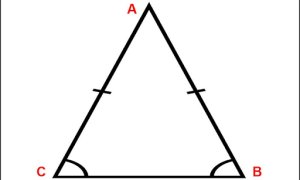
Tính chất tam giác cân
Trong tam giác cân, hai góc ở đáy bằng nhau.
Ngược lại, nếu một tam giác có hai góc bằng nhau thì tam giác đó cân.
Tam giác đều là tam giác cân có ba cạnh bằng nhau.
Ví dụ
Cho ΔABC có AB = AC. Khi đó ΔABC là tam giác cân tại A.
Cho ΔABC có ∠ABC = ∠ACB. Khi đó ΔABC là tam giác cân.
Dấu hiệu nhận biết tam giác cân
Dấu hiệu dựa vào cạnh
– Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân.
Ví dụ:
Cho ΔABC có AB = AC. Khi đó ΔABC là tam giác cân tại A.
Dấu hiệu dựa vào góc
– Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.
Ví dụ:
Cho ΔABC có ∠ABC = ∠ACB. Khi đó ΔABC là tam giác cân tại A.
Dấu hiệu dựa vào đường trung tuyến
– Nếu đường trung tuyến ứng với một cạnh của tam giác bằng nửa cạnh đó thì tam giác đó là tam giác cân.
Ví dụ:
Cho ΔABC có AM là đường trung tuyến ứng với cạnh BC và \(AM = \frac{BC}{2}\). Khi đó ΔABC là tam giác cân tại A.
Dấu hiệu dựa vào đường cao
– Nếu đường cao ứng với một cạnh của tam giác cũng là đường phân giác của góc ở đỉnh ứng với cạnh đó thì tam giác đó là tam giác cân.
Ví dụ:
Cho ΔABC có AH là đường cao ứng với cạnh BC và AH cũng là đường phân giác của ∠BAC. Khi đó ΔABC là tam giác cân tại A.
Những dấu hiệu nhận biết khác
Trường hợp bằng nhau cạnh – cạnh – cạnh (c.c.c):
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Trường hợp bằng nhau cạnh – góc – cạnh (c.g.c):
Nếu hai cạnh của tam giác này bằng hai cạnh của tam giác kia và hai góc xen giữa các cạnh đó bằng nhau thì hai tam giác đó bằng nhau.
Trường hợp bằng nhau góc – cạnh – góc (g.c.g):
Nếu hai góc của tam giác này bằng hai góc của tam giác kia và cạnh tương ứng giữa hai góc bằng nhau thì hai tam giác đó bằng nhau.
Ví dụ:
Cho ΔABC và ΔMNP có AB = MN, AC = MP, ∠BAC = ∠MNP. Khi đó ΔABC = ΔMNP (c.g.c)
Suy ra: ΔABC và ΔMNP là hai tam giác cân.
Bài tập vận dụng tam giác cân
Bài 1: Cho tam giác ABC cân tại A, biết AB = AC = 5cm, BC = 6cm. Tính các góc của tam giác ABC.
Lời giải:
Áp dụng tính chất tam giác cân, ta có:
∠ABC = ∠ACB = \(\frac{180° – ∠BAC}{2}\)
Áp dụng định lý cosin vào tam giác ABC, ta có:
cos∠BAC = \(\frac{AB² + AC² – BC²}{2AB.AC} = \frac{5² + 5² – 6²}{2.5.5 = 1/5}\)
∠BAC = \(arccos(\frac{1}{5}) ≈ 72°\)
Thay ∠BAC vào biểu thức trên, ta được:
∠ABC = ∠ACB = \(\frac{180° – 72°}{2} = 54°\)
Vậy ∠BAC = 72°, ∠ABC = ∠ACB = 54°.
Bài 2: Cho tam giác ABC cân tại A, biết ∠BAC = 40°. Tính các góc còn lại của tam giác ABC.
Lời giải:
Áp dụng tính chất tam giác cân, ta có:
∠ABC = ∠ACB = \(\frac{180° – ∠BAC}{2}\)
Thay ∠BAC vào biểu thức trên, ta được:
∠ABC = ∠ACB = \(\frac{180° – 40°}{2} = 70°\)
Vậy ∠ABC = ∠ACB = 70° và ∠BAC = 40°.
Bài 3: Cho tam giác ABC cân tại A, đường trung tuyến AM. Chứng minh AM là đường phân giác của ∠BAC.
Lời giải:
Xét ΔAMB và ΔAMC, ta có:
AB = AC (tam giác ABC cân tại A)
AM là cạnh chung
BM = MC (AM là đường trung tuyến)
Vậy ΔAMB = ΔAMC (c.g.c)
Suy ra: ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = ∠BAC (góc kề bù)
Suy ra: ∠AMB = ∠AMC = \(\frac{∠BAC}{2}\)
Hay ∠BAM = ∠CAM
Vậy AM là đường phân giác của ∠BAC.
Luyện tập
- Cho tam giác ABC cân tại A, biết AB = AC = 4cm, BC = 6cm. Tính các góc của tam giác ABC.
- Cho tam giác ABC cân tại A, biết ∠BAC = 50°. Tính các góc còn lại của tam giác ABC.
- Cho tam giác ABC cân tại A, đường phân giác AD. Chứng minh AD là đường trung tuyến của tam giác ABC.
- Cho tam giác ABC cân tại A, đường cao AH. Chứng minh AH là đường trung tuyến của tam giác ABC.
- Cho tam giác ABC cân tại A, đường trung tuyến AM. Biết AM = 5cm, BC = 8cm. Tính AB và AC.
- Cho tam giác ABC cân tại A, đường cao AH. Biết AH = 4cm, BC = 10cm. Tính AB và AC.
- Cho tam giác ABC cân tại A, đường phân giác AD. Biết AD = 4cm, BC = 8cm. Tính AB và AC.
- Cho tam giác ABC cân tại A, đường cao AH. Biết AH = 3cm, BC = 6cm. Tính AB và AC.
- Cho tam giác ABC cân tại A, biết AB = AC = 5cm, BC = 8cm. Vẽ đường trung tuyến AM. Tính AM.
- Cho tam giác ABC cân tại A, biết AB = AC = 6cm, BC = 10cm. Vẽ đường cao AH. Tính AH.
Tóm lại, tam giác cân là một khái niệm quan trọng trong môn Toán học lớp 7. Nó có nhiều tính chất và ứng dụng trong thực tế. Việc nắm vững kiến thức về tam giác cân là rất cần thiết để giải các bài toán liên quan.








