Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu là một chủ đề quan trọng trong chương trình Toán lớp 7. Kiến thức về chủ đề này giúp học sinh hiểu rõ hơn về mối liên hệ giữa các đường thẳng trong mặt phẳng, từ đó giải quyết các bài toán liên quan một cách hiệu quả.
Định nghĩa quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
Đường vuông góc: Là đường thẳng đi qua một điểm và tạo với đường thẳng cho trước một góc 90°.
Đường xiên: Là đường thẳng không vuông góc với đường thẳng cho trước.
Hình chiếu: Là chân đường vuông góc kẻ từ một điểm trên đường xiên đến đường thẳng cho trước.
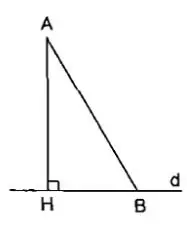
Định lý
Định lý 1: Trong các đường xiên và đường vuông góc kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
Hệ quả
Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau và ngược lại.
Nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.
Định lý 2: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó:
Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
Đường xiên nào lớn hơn thì có hình chiếu lớn hơn.
Ví dụ 1: Cho tam giác ABC vuông tại A, AB = 3cm, AC = 4cm. Tính BC.
Giải:
Áp dụng định lý Pitago, ta có:
\(BC² = AB² + AC² = 3² + 4² = 25\)⇒ \(BC = \sqrt{25} = 5cm\)
Ví dụ 2: Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Kẻ AH vuông góc với BC (H thuộc BC). Tính BH, HC.
Giải:
Áp dụng định lý 1, ta có: AH < AB
⇒ BH = BC – AH = BC – AB = 8 – 6 = 2cm
Áp dụng hệ quả của định lý 1, ta có:
AB = AC ⇒ BH = HC
⇒ HC = BC – BH = 8 – 2 = 6cm
Các đường xiên và hình chiếu của chúng
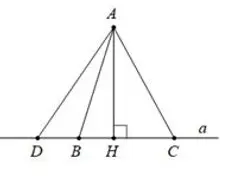
Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó:
Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
AH ⊥ a, HD > HC ⇒ AD > AC
Đường xiên nào lớn hơn thì có hình chiếu lớn hơn.
AH ⊥ a, AD > AC ⇒ HD > HC
Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau; nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.
AB = AC ⇔ HB = HC
Quan hệ giữa đường vuông góc và đường xiên
Đường vuông góc: Là đường thẳng đi qua một điểm và tạo với đường thẳng cho trước một góc 90°.
Đường xiên: Là đường thẳng không vuông góc với đường thẳng cho trước.
Ví dụ 1: Cho tam giác ABC vuông tại A, AB = 3cm, AC = 4cm. Tính BC.
Giải:
Áp dụng định lý Pitago, ta có:
\(BC² = AB² + AC² = 3² + 4² = 25\)⇒ \(BC = \sqrt{25} = 5cm\)
Ví dụ 2: Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Kẻ AH vuông góc với BC (H thuộc BC). Tính BH, HC.
Giải:
Áp dụng định lý 1, ta có:
AH < AB
⇒ BH = BC – AH = BC – AB = 8 – 6 = 2cm
Áp dụng hệ quả của định lý 1, ta có:
AB = AC ⇒ BH = HC
⇒ HC = BC – BH = 8 – 2 = 6cm
Các dạng bài tập và phương pháp giải
Dạng 1: Chứng minh
Ví dụ: Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Kẻ AH vuông góc với BC (H thuộc BC). Chứng minh rằng:
- AH < AB
- BH = HC
Phương pháp giải:
Chứng minh AH < AB:
Sử dụng định lý: Trong các đường xiên và đường vuông góc kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
Chứng minh BH = HC:
Sử dụng hệ quả của định lý: Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau.
Dạng 2: Tính toán
Ví dụ: Cho tam giác ABC vuông tại A, AB = 8cm, AC = 15cm. Kẻ AH vuông góc với BC (H thuộc BC). Tính BH, HC.
Phương pháp giải:
- Áp dụng định lý Pitago để tính BC.
- Áp dụng hệ quả của định lý: Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau.
- Áp dụng định lý: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó, thì đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
Dạng 3: Vận dụng
Ví dụ: Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Kẻ AH vuông góc với BC (H thuộc BC). Một điểm M nằm trên cạnh BC. Chứng minh rằng:
\(MA² + MH² > MB² + MH²\)Phương pháp giải:
- Sử dụng định lý Pitago và hệ quả của định lý: Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau.
- So sánh hai tam giác vuông AMH và BMH.
Dạng 4: Bài toán thực tế
Ví dụ: Một cái thang dài 4m được đặt dựa vào một bức tường. Biết rằng khoảng cách từ chân thang đến tường là 3m. Tính độ cao của bức tường (tính từ mặt đất đến điểm tiếp xúc với thang).
Phương pháp giải: Áp dụng định lý Pitago để tính độ cao của bức tường.
Bài tập có lời giải chi tiết về Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu lớp 7
Bài 1: Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Kẻ AH vuông góc với BC (H thuộc BC). Tính BH, HC.
Giải:
Áp dụng định lý Pitago, ta có:
\(BC² = AB² + AC² = 6² + 8² = 100\)
⇒ \(BC = \sqrt{100} = 10cm
Áp dụng hệ quả của định lý 1, ta có:
AB < AC ⇒ BH < HC
Áp dụng định lý 2, ta có:
[latex]\frac{BH}{AB} = \frac{HC}{AC}\)
⇒ \(\frac{BH}{6} = \frac{HC}{8}\)
⇒ \(\frac{BH}{HC} = \frac{6}{8} = \frac{3}{4}\)
Áp dụng tính chất tỉ lệ thức, ta có:
\(BH = \frac{3}{7} * (BH + HC) = \frac{3}{7} * 10 = 4,29cm\)
\(HC = \frac{4}{7} * (BH + HC) = \frac{4}{7} * 10 = 5,71cm\)
Bài 2: Cho tam giác ABC vuông tại A, AB = 8cm, AC = 15cm. Kẻ AH vuông góc với BC (H thuộc BC). Tính BH, HC.
Giải:
Áp dụng định lý Pitago, ta có:
\(BC² = AB² + AC² = 8² + 15² = 289\)
⇒ \(BC = \sqrt{289} = 17cm\)
Áp dụng hệ quả của định lý 1, ta có:
AB < AC ⇒ BH < HC
Áp dụng định lý 2, ta có:
\(\frac{BH}{AB} = \frac{HC}{AC}\)
⇒ \(\frac{BH}{8} = \frac{HC}{15}\)
⇒ \(\frac{BH}{HC} = \frac{8}{15}\)
Áp dụng tính chất tỉ lệ thức, ta có:
\(BH = 8/23 * (BH + HC) = 8/23 * 17 = 6,09\)cm
\(HC = 15/23 * (BH + HC) = 15/23 * 17 = 10,91\)cm
Bài 3: Cho tam giác ABC vuông tại A, AB = 5cm, AC = 12cm. Kẻ AH vuông góc với BC (H thuộc BC). Tính BH, HC.
Giải:
Áp dụng định lý Pitago, ta có:
\(BC² = AB² + AC² = 5² + 12² = 169\)
⇒ \(BC = \sqrt{169} = 13\)cm
Áp dụng hệ quả của định lý 1, ta có:
AB < AC ⇒ BH < HC
Áp dụng định lý 2, ta có:
\(\frac{BH}{AB} = \frac{HC}{AC}\)
⇒\(\frac{BH}{5} = \frac{HC}{12}\)
⇒ \(\frac{BH}{HC} = \frac{5}{12}\)
Áp dụng tính chất tỉ lệ thức, ta có:
\(BH =\frac{5}{17} * (BH + HC) = \frac{5}{17} * 13 = 3,82cm\)
\(HC = \frac{12}{17} * (BH + HC) = \frac{12}{17} * 13 = 7,65cm\)
Học sinh cần nắm vững các định nghĩa, định lý và hệ quả liên quan đến chủ đề này để có thể áp dụng vào giải bài tập một cách chính xác.
