Phương trình đường elip là một chủ đề quan trọng trong chương trình Toán 10, được ứng dụng trong nhiều lĩnh vực như vật lý, kỹ thuật, kiến trúc,… Bài viết này sẽ trình bày chi tiết về phương trình đường elip
Định nghĩa phương trình đường elip
Elip là tập hợp tất cả các điểm M sao cho tổng MF1 + MF2 = 2a (a > 0) không đổi, với F1 và F2 là hai điểm cố định (gọi là tiêu điểm).
Phương trình đường elip chính tắc
Elip có tâm O, hai trục đối xứng Ox và Oy, hai tiêu điểm F1(-c, 0) và F2(c, 0) có phương trình:
\(x²/a² + y²/b² = 1\)
Elip có tâm O, tiêu cự 2c, độ lệch tâm f = c/a:
\(x^2 / (a^2 – c^2) + y^2 / b^2 = 1\)
- Trong đó:
- a là nửa trục lớn (a > 0)
- b là nửa trục nhỏ (b > 0)
- c = √(a² – b²) là độ dài tiêu cự
Vẽ elip
Sử dụng phương trình chính tắc:
- Xác định tâm O(0, 0), hai tiêu điểm F1(-c, 0) và F2(c, 0).
- Vẽ hai đường tròn tâm O bán kính a và b.
- Elip là giao điểm của hai đường tròn.
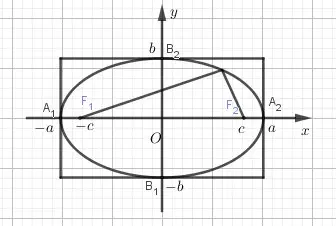
Tính chất đường elip
- Elip nhận trục Ox và Oy làm trục đối xứng.
- Elip có hai tiêu điểm F1 và F2 nằm trên trục Ox, cách O một khoảng c.
- Tích số PF1.PF2 = \(a^2 – b^2\) với mọi điểm P thuộc elip.
- Elip có 4 đỉnh A1, A2, B1, B2.
- Elip có 2 đường chuẩn:
\(x = ± a^2 / c\)
Vị trí tương đối
Cho điểm M(x; y) và elip (E):
- M nằm trên (E) ⇔ \((x^2 / a^2) + (y^2 / b^2) = 1\)
- M nằm trong (E) ⇔ \((x^2 / a^2) + (y^2 / b^2) < 1\)
- M nằm ngoài (E) ⇔ \((x^2 / a^2) + (y^2 / b^2) > 1\)
Lời giải chi tiết các bài tập về phương trình đường elip
Dạng 1: Tìm tâm, trục lớn, trục nhỏ, tiêu cự, độ lệch tâm của elip:
Bài 1: Cho phương trình elip: \(x²/9 + y²/4 = 1\). Tìm tâm, trục lớn, trục nhỏ, tiêu cự, độ lệch tâm của elip.
Lời giải:
- Elip có tâm O(0; 0).
- Trục lớn 2a = 10, trục nhỏ 2b = 8.
- Tiêu cự \(2c = √(a² – b²) = √(10² – 8²) = 6\).
- Độ lệch tâm \(e = c/a = 6/10 = 3/5\).
Bài 2: Cho điểm M(3; 2) và elip (E):\( x²/16 + y²/9 = 1\). Tìm tọa độ các tiêu điểm của elip (E).
Lời giải:
- Elip có tâm O(0; 0), trục lớn 2a = 8, trục nhỏ 2b = 6.
- Tiêu cự \(2c = √(a² – b²) = √(8² – 6²) = 2√7\).
- Tọa độ các tiêu điểm F₁(-√7; 0) và F₂(√7; 0).
- Do M(3; 2) nằm trên trục lớn của elip, nên \(MF₁² + MF₂² = 3² + (2 – √7)² + 3² + (2 + √7)² = 16 + 9 = 25\).
- Vậy MF₁ = MF₂ = 5.
Dạng 2: Viết phương trình đường elip:
Bài 3: Viết phương trình đường elip có tâm O(0; 0), trục lớn 2a = 10, trục nhỏ 2b = 8.
Lời giải:
Phương trình chính tắc của elip: \(x²/5² + y²/4² = 1\).
Bài 4: Viết phương trình đường elip đi qua điểm A(3; 4) và có tiêu cự 2c = 10.
Lời giải:
- Elip có tâm O(0; 0), trục lớn 2a = 10, trục nhỏ \(2b = √(a² – c²) = √(10² – 5²) = 5√3\).
- Phương trình chính tắc của elip: \(x²/5² + y²/(5√3)² = 1\).
- Thay tọa độ điểm A(3; 4) vào phương trình, ta có: \(3²/5² + 4²/(5√3)² = 1\).
- Vậy phương trình đường elip là: \(x²/5² + y²/(5√3)² = 1\).
Dạng 3: Xác định vị trí tương đối của điểm và elip:
Bài 5: Cho điểm M(2; 3) và elip (E): \(x²/9 + y²/4 = 1\). Xác định vị trí tương đối của điểm M và elip (E).
Lời giải:
- Ta có: \(MF₁² = (2 + √7)² + (3 – 0)² = 16 + 9 + 14√7 = 39 + 14√7\).
- \(MF₂² = (2 – √7)² + (3 – 0)² = 16 + 9 – 14√7 = 39 – 14√7\).
- Vì \(MF₁² > 9 và MF₂² > 9\), nên điểm M nằm bên ngoài elip (E).
Bài viết này đã cung cấp cho bạn những kiến thức cơ bản về phương trình đường elip. Hy vọng những kiến thức này sẽ giúp bạn học tập và giải các bài toán liên quan đến elip một cách hiệu quả.
