Phép quay là một phép biến hình quan trọng trong chương trình Toán 11, đóng vai trò nền tảng cho nhiều chủ đề khác như: vectơ, hệ tọa độ, geometria giải tích,…
Phép quay được ứng dụng rộng rãi trong nhiều lĩnh vực như toán học, vật lý, kỹ thuật, kiến trúc,… Bài viết này sẽ trình bày khái niệm, tính chất và ứng dụng của phép quay.
Định nghĩa của phép quay
- Phép quay: Cho điểm O và góc lượng giác α. Phép biến hình biến điểm O thành chính nó, biến mỗi điểm M khác O thành điểm M’ sao cho OM’ = OM và góc lượng giác (OM; OM’) bằng α được gọi là phép quay tâm O góc α.
- Điểm O: Gọi là tâm quay.
- Góc α: Gọi là góc quay.
- Ký hiệu: Q(O, α).
Tính chất của phép quay
- Phép quay bảo toàn khoảng cách: Khoảng cách giữa hai điểm bất kỳ A và B được bảo toàn qua phép quay.
- Phép quay biến đường thẳng thành đường thẳng: Đường thẳng d biến thành đường thẳng d’ qua phép quay, với d’ là ảnh của d qua phép quay.
- Phép quay biến đoạn thẳng thành đoạn thẳng bằng nó: Đoạn thẳng AB biến thành đoạn thẳng A’B’ qua phép quay, với A’B’ = AB.
- Phép quay biến tam giác thành tam giác bằng nó: Tam giác ABC biến thành tam giác A’B’C’ qua phép quay, với A’B’C’ = ABC.
- Phép quay biến đường tròn thành đường tròn có cùng bán kính: Đường tròn (C;R) biến thành đường tròn (C’;R) qua phép quay, với C’ là ảnh của C qua phép quay.
Công thức phép quay
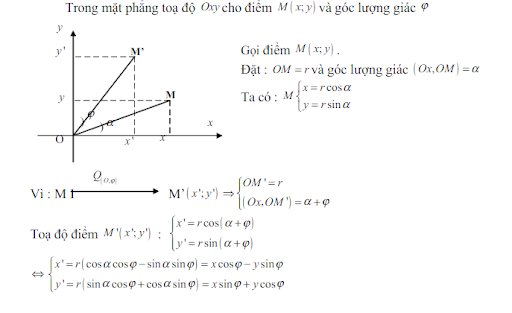
Các dạng bài tập về phép quay lớp 11 và phương pháp giải
Xác định ảnh của điểm, đoạn thẳng, đường thẳng, tam giác,… qua phép quay
Phương pháp giải:
- Sử dụng định nghĩa phép quay để xác định ảnh của điểm.
- Sử dụng tính chất phép quay để xác định ảnh của đoạn thẳng, đường thẳng, tam giác.
- Sử dụng công thức tọa độ điểm ảnh để xác định ảnh của điểm qua phép quay tâm O góc α.
Tìm tọa độ điểm; phương trình đường thẳng, đường tròn qua phép quay
Phương pháp giải:
- Sử dụng công thức tọa độ điểm ảnh để tìm tọa độ điểm qua phép quay.
- Sử dụng tính chất phép quay để tìm phương trình đường thẳng, đường tròn qua phép quay.
Chứng minh hai hình bằng nhau bằng phép quay
Phương pháp giải:
- Chứng minh hai hình có cùng số đo các cạnh tương ứng.
- Chứng minh hai hình có cùng số đo các góc tương ứng.
- Sử dụng phép quay để biến hình này thành hình kia.
Ứng dụng phép quay để giải bài toán hình học
Phương pháp giải:
- Vẽ hình và xác định các điểm, đường thẳng liên quan qua phép quay.
- Sử dụng tính chất phép quay để giải bài toán.
Ví dụ:
Cho điểm A(1,2) và phép quay tâm O(0,0) góc 90°. Tìm ảnh A’ của điểm A qua phép quay.
Giải:
- Sử dụng công thức tọa độ điểm ảnh, ta có:
\(x’ = 1.cos(90°) – 2.sin(90°) + 0 = -2\)
\(y’ = 1.sin(90°) + 2.cos(90°) + 0 = 1\)
- Vậy ảnh A’ của điểm A qua phép quay là A'(-2,1).
Cho đường thẳng d: x + y – 2 = 0 và phép quay tâm O(0,0) góc 45°. Tìm phương trình đường thẳng d’ ảnh của đường thẳng d qua phép quay.
Giải:
- Gọi M là một điểm bất kỳ trên đường thẳng d.
- Ảnh M’ của điểm M qua phép quay là điểm M'(x’,y’) thỏa mãn:
\(x’ = x.cos(45°) – y.sin(45°)\)
\(y’ = x.sin(45°) + y.cos(45°)\)
Thay x và y vào phương trình đường thẳng d, ta có:
\(x’ + y’ – 2 = 0\)
- Vậy phương trình đường thẳng d’ ảnh của đường thẳng d qua phép quay là x + y – 2 = 0.
Cho tam giác ABC với A(1,2), B(3,4) và C(5,6). Chứng minh rằng tam giác ABC bằng tam giác A’B’C’ với A'(2,1), B'(4,3) và C'(6,5).
Giải:
Ta có:
OA = OA’ = OB = OB’ = OC = OC’
- Gọi M là trung điểm của BC.
- Ảnh M’ của điểm M qua phép quay tâm O góc 180° là điểm M’ trùng với M.
- Do đó, tam giác ABC bằng tam giác A’B’C’ qua phép quay tâm O góc 180°.
Cho hình vuông ABCD với cạnh a. Một con kiến di chuyển từ đỉnh A theo đường chéo AC đến đỉnh C. Hỏi con kiến di chuyển quãng đường ngắn nhất bằng bao nhiêu?
Giải:
- Gọi O là tâm hình vuông ABCD.
- Phép quay tâm O góc 45° biến A thành C.
- Do đó, quãng đường ngắn nhất con kiến di chuyển là AC’ = a√2.
Bài tập luyện tập về phép quay
Bài 1: Cho điểm A(1, 2) và phép quay tâm O(0, 0) góc 135°. Tìm ảnh A’ của điểm A qua phép quay.
Bài 2: Cho đường thẳng d: x – y + 1 = 0 và phép quay tâm O(0, 0) góc 60°. Tìm phương trình đường thẳng d’ ảnh của đường thẳng d qua phép quay.
Bài 3: Cho tam giác ABC với A(1, 2), B(3, 4) và C(5, 6). Chứng minh rằng tam giác ABC bằng tam giác A’B’C’ với A'(1, -2), B'(3, -4) và C'(5, -6) qua phép quay tâm O(0, 0) góc 180°.
Bài 4: Cho hình vuông ABCD với cạnh a. Một con kiến di chuyển từ đỉnh A theo đường thẳng đi qua B đến đỉnh C. Hỏi con kiến di chuyển quãng đường ngắn nhất bằng bao nhiêu?
Bài 5: Cho tam giác ABC vuông tại A với AB = 3 cm và AC = 4 cm. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC. Tìm ảnh B’ của điểm B qua phép quay tâm O góc 45°.
Gợi ý giải:
Bài 1:
Sử dụng công thức tọa độ điểm ảnh.
Bài 2:
- Gọi M là một điểm bất kỳ trên đường thẳng d.
- Sử dụng tính chất phép quay để tìm ảnh M’ của điểm M.
- Thay tọa độ điểm M’ vào phương trình đường thẳng d để tìm phương trình đường thẳng d’.
Bài 3:
- Chứng minh OA = OA’ = OB = OB’ = OC = OC’.
- Gọi M là trung điểm của BC.
- Chứng minh ảnh M’ của điểm M qua phép quay tâm O góc 180° là điểm M’ trùng với M.
Bài 4:
- Gọi O là tâm hình vuông ABCD.
- Sử dụng tính chất phép quay để tìm ảnh A’ của điểm A qua phép quay tâm O góc 45°.
- Tính độ dài đoạn thẳng AC’.
Bài 5:
- Gọi D là điểm đối xứng với B qua O.
- Sử dụng tính chất phép quay để tìm ảnh B’ của điểm B qua phép quay tâm O góc 45°.
Phép quay là một phép biến hình quan trọng và có nhiều ứng dụng trong thực tế. Việc nắm vững kiến thức về phép quay giúp chúng ta giải quyết các bài toán hình học một cách hiệu quả và có nhiều ứng dụng trong các lĩnh vực khác nhau. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức bổ ích về phép quay.








