Mặt tròn xoay là một chủ đề quan trọng trong chương Hình đa diện của môn Toán lớp 12. Chủ đề này bao gồm các khái niệm cơ bản về mặt tròn xoay, các loại mặt tròn xoay phổ biến, công thức tính diện tích và thể tích của các mặt tròn xoay, và các bài toán ứng dụng.
Khái niệm mặt tròn xoay
- Mặt tròn xoay là một mặt được tạo thành khi quay một đường cong (đường sinh) quanh một đường thẳng cố định (trục).
- Mặt phẳng kinh tuyến là mặt phẳng qua trục và vuông góc với đường sinh tại một điểm M bất kỳ của đường sinh.
- Góc ở đỉnh của mặt nón tròn xoay là góc tạo bởi hai đường sinh qua một điểm trên trục.
Công thức tính diện tích mặt tròn xoay
Hình nón tròn xoay
- Diện tích xung quanh: \(Sxq = πrl\) trong đó: * r là bán kính đáy * l là độ dài đường sinh
- Diện tích toàn phần: \(Stp = πr(r + l)\)
Hình trụ tròn xoay
- Diện tích xung quanh: \(Sxq = 2πrh\) trong đó: * r là bán kính đáy * h là chiều cao
- Diện tích toàn phần: \(Stp = 2πrh + 2πr²\)
Mặt nón cụt
- Diện tích xung quanh: \(Sxq = π(R + r)l\) trong đó: * R là bán kính đáy lớn * r là bán kính đáy nhỏ * l là độ dài đường sinh
- Diện tích toàn phần: \(Stp = π(R + r)l + π(R² + r²)\)
Ví dụ áp dụng
Ví dụ 1: Một hình nón có bán kính đáy r = 5 cm và chiều cao h = 12 cm. Tính diện tích xung quanh và diện tích toàn phần của hình nón.
Lời giải:
- Diện tích xung quanh: \(Sxq = πrl = π.5.12 = 60π\) cm²
- Diện tích toàn phần: \(Stp = πr(r + l) = π.5(5 + 12) = 85π\) cm²
Ví dụ 2: Một hình trụ có bán kính đáy r = 3 cm và chiều cao h = 10 cm. Tính diện tích xung quanh và diện tích toàn phần của hình trụ.
Lời giải:
- Diện tích xung quanh: \(Sxq = 2πrh = 2π.3.10 = 60π\) cm²
- Diện tích toàn phần: \(Stp = 2πrh + 2πr² = 2π.3.10 + 2π.3² = 126π\) cm²
Phân loại mặt tròn xoay
- Hình nón tròn xoay:
- Là mặt tròn xoay được tạo thành khi quay một đường thẳng (đường sinh) quanh một đường thẳng cố định (trục).
- Góc ở đỉnh của hình nón tròn xoay là góc tạo bởi hai đường sinh qua một điểm trên trục.
- Hình trụ tròn xoay:
- Là mặt tròn xoay được tạo thành khi quay một đường thẳng (đường sinh) quanh một đường thẳng cố định (trục) và song song với đường sinh.
- Bán kính của hình trụ tròn xoay là khoảng cách từ trục đến đường sinh.
- Mặt nón cụt: Là phần của hình nón tròn xoay được giới hạn bởi hai mặt phẳng cắt hình nón, một mặt phẳng vuông góc với trục và một mặt phẳng cắt chéo trục.
Ứng dụng của mặt tròn xoay
- Kiến trúc: Các mái vòm, mái chóp, cột trụ… thường được thiết kế dựa trên hình nón và hình trụ.
- Kỹ thuật: Các chi tiết máy móc như bánh răng, trục, lò xo… thường được chế tạo dựa trên hình trụ.
- Khoa học máy tính: Các mô hình 3D trong đồ họa máy tính thường được tạo ra từ các mặt tròn xoay.
Các đặc điểm chung của mặt tròn xoay
Khái niệm
Mặt tròn xoay là mặt được tạo thành khi quay một đường cong (đường sinh) quanh một đường thẳng cố định (trục).
Các yếu tố
- Trục: Là đường thẳng cố định mà đường sinh quay quanh.
- Đường sinh: Là đường cong quay quanh trục để tạo thành mặt tròn xoay.
- Mặt phẳng kinh tuyến: Là mặt phẳng qua trục và vuông góc với đường sinh tại một điểm M bất kỳ của đường sinh.
Phân loại
Mặt tròn xoay được phân loại thành 3 loại chính:
- Hình nón tròn xoay: Là mặt tròn xoay được tạo thành khi quay một đường thẳng (đường sinh) quanh một đường thẳng cố định (trục).
- Hình trụ tròn xoay: Là mặt tròn xoay được tạo thành khi quay một đường thẳng (đường sinh) quanh một đường thẳng cố định (trục) và song song với đường sinh.
- Mặt nón cụt: Là phần của hình nón tròn xoay được giới hạn bởi hai mặt phẳng cắt hình nón, một mặt phẳng vuông góc với trục và một mặt phẳng cắt chéo trục.
Đặc điểm chung
- Mọi điểm trên mặt tròn xoay đều cách đều trục.
- Mọi mặt phẳng kinh tuyến đều cắt mặt tròn xoay theo một đoạn thẳng.
- Mặt tròn xoay có thể được trải phẳng thành một hình phẳng.
Các dạng bài tập về khối đa diện
Dạng bài tập về tính số đỉnh, số cạnh, số mặt của hình đa diện
- Cho một hình đa diện, tính số đỉnh, số cạnh, số mặt của nó.
- Cho số đỉnh, số cạnh, số mặt của một hình đa diện, tìm điều kiện để hình đa diện đó tồn tại.
Ví dụ:
Cho hình lăng trụ tam giác ABC.A’B’C’.
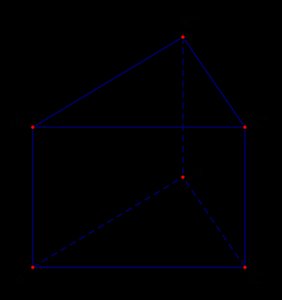
- a) Tính số đỉnh, số cạnh, số mặt của hình lăng trụ.
- b) Kể tên các mặt của hình lăng trụ.
Lời giải:
a) Hình lăng trụ tam giác ABC.A’B’C’ có:
- 9 đỉnh: A, B, C, A’, B’, C’, M, N, P.
- 15 cạnh: AB, BC, CA, A’B’, B’C’, C’A’, AA’, BB’, CC’, AM, BM, CM, A’N, B’N, C’N.
- 6 mặt: (ABC), (A’B’C’), (ABB’A’), (BCC’B’), (ACC’A’), (AMN).
b) Các mặt của hình lăng trụ là:
- (ABC)
- (A’B’C’)
- (ABB’A’)
- (BCC’B’)
- (ACC’A’)
- (AMN)
Dạng bài tập về tính diện tích và thể tích của hình đa diện
- Cho một hình đa diện, tính diện tích toàn phần và thể tích của nó.
- Cho diện tích toàn phần hoặc thể tích của một hình đa diện, tìm điều kiện để hình đa diện đó tồn tại.
Ví dụ:
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = 2a, cạnh bên SA = 3a.
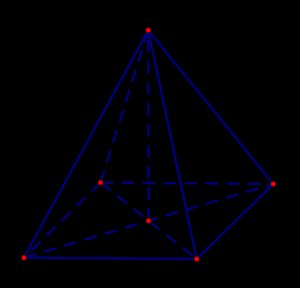
- a) Tính diện tích toàn phần của hình chóp.
- b) Tính thể tích của hình chóp.
Lời giải:
- a) Diện tích toàn phần của hình chóp S.ABCD là:
\(S = Sxq + Stp = (1/2).4a.3a + 4.(a²√2)/2 = 12a²√2 + 2a²\)
- b) Thể tích của hình chóp S.ABCD là:
\(V = (1/3).4a².(3a) = 4a³\)
Dạng bài tập về tính khoảng cách
- Tính khoảng cách giữa hai điểm bất kỳ trong một hình đa diện.
- Tính khoảng cách từ một điểm đến một mặt phẳng trong một hình đa diện.
Ví dụ:
Cho hình lăng trụ tam giác ABC.A’B’C’.
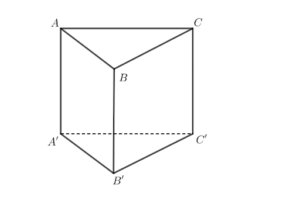
- a) Tính khoảng cách giữa hai điểm A và C’.
- b) Tính khoảng cách từ điểm B đến mặt phẳng (A’B’C’).
Lời giải:
- a) Khoảng cách giữa hai điểm A và C’ là:
\(AC’ = √(AA’² + C’C²) = √(a² + 3a²) = 2a√2\)
- b) Khoảng cách từ điểm B đến mặt phẳng (A’B’C’) là:
\(h = BB’/(A’B’.n) = a/(√(a² + b² + c²))\)
Mặt tròn xoay là một chủ đề thú vị và bổ ích trong chương trình Toán lớp 12. Qua việc học tập chủ đề này, học sinh sẽ củng cố kiến thức về hình học không gian, phát triển tư duy logic và khả năng ứng dụng kiến thức vào thực tế.








