Tổng hợp kiến thức về khảo sát sự biến thiên của hàm số

Khảo sát sự biến thiên của hàm số là việc xác định các tính chất biến thiên của hàm số như đồng biến, nghịch biến, cực trị, điểm uốn, điểm gấp khúc… dựa vào đồ thị hoặc biểu thức của hàm số.

Mục lục

Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Khảo sát sự biến thiên và vẽ đồ thị hàm số y = ax³ + bx² + cx + d

Phương pháp giải

Tập xác định: D=R
Tính y’ và cho y’ = 0. ( y = 0 hoặc có 2 nghiệm, hoặc có nghiệm kép, hoặc vô nghiệm)
Tính các giới hạn limx->+∞+ f(x), limx->-∞ f(x).

Lập bảng biển thiên:

Nếu y’ = 0 có hai nghiệm thì dấu của ý là: “Trong trái ngoài cùng”.
Nếu y’ = 0 có nghiệm kép thì dấu của ý là: “Luôn cùng dấu với a “ (Ngoại trừ tại nghiệm kép)
Nếu y’ = 0 vô nghiệm thì dấu của ý là: “Luôn cùng dấu với a”

Kết luận:

Tính chất đơn điệu của hàm số.
Cực trị của hàm số.

Tính y” và cho y” = 0. Suy ra điểm uốn.
Chọn hai điểm đặc biệt của đồ thị.
Vẽ đồ thị: Đồ thị có 6 dạng và luôn luôn nhận điểm uốn làm tâm đối xứng.

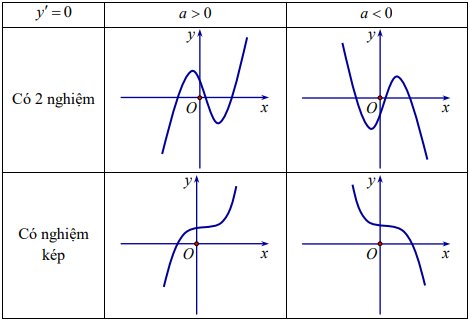
khảo sát sự biến thiên của hàm số

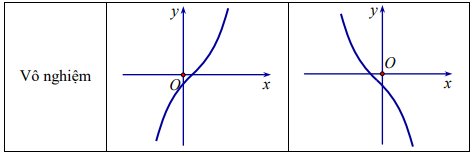
Khảo sát sự biến thiên và vẽ đô thị hàm số y = ax + bx² + c

Tập xác định: D=R
Tính y và cho y’=0 (y’= 0 có 3 nghiệm, hoặc có 1 nghiệm và luôn có nghiệm x=0)
Lập bảng biến thiên: “Bên phải bảng biển thiên, dấu ý luôn luôn cùng dầu với a”
Kết luận:

Tính chất đơn điệu của hàm số.
Cực trị của hàm số.
Giới hạn của hàm số.

Chọn hai điểm đặc biệt của đồ thị.
Vẽ đồ thị: Đồ thị có 4 dạng và luôn luôn nhận điểm uốn làm tâm đối xứng.

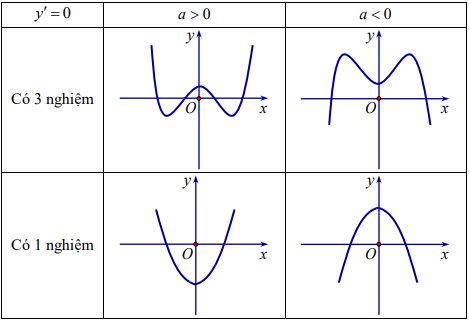
Khảo sát sự biến thiên và vẽ

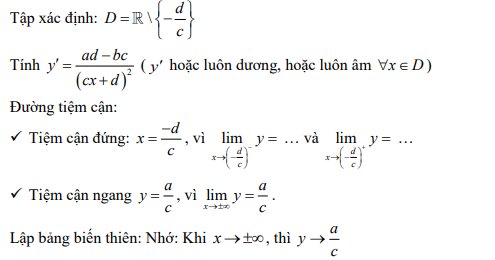
“Nghĩa là hai đầu của bảng biến thiên là giá trị của tiệm cận ngang”

Kết luận:

Hàm số luôn đồng biến trên từng khoảng xác định hoặc luôn nghịch biến trên từng khoảng xác định.
Hàm số không có cực trị.

Chọn ít nhất 4 điểm đặc biệt của đồ thị và phải có toạ độ giao điểm của đồ thị với 2 trục toạ độ.
Vẽ đồ thị: Đồ thị có 2 dạng và luôn luôn nhận giao điểm của hai đường tiệm cận là tâm đối xứng.
Vẽ đồ thị: Đồ thị có 2 dạng và luôn luôn nhận điểm uốn làm tâm đối xứng.

Bài tập về khảo sát sự biến thiên của hàm số có lời giải chi tiết

Bài 1. Cho hàm số f(x) = x3−3x2 + 2x−5.

a) Khảo sát sự biến thiên của hàm số f(x).
b) Vẽ đồ thị hàm số f(x).

Lời giải:

a) Khảo sát sự biến thiên:

Tập xác định: D = R.
Đạo hàm: f′(x)=3×2−6x+2.
Bảng biến thiên:

Khoảng	f'(x)	Kết luận
(−∞;1)	f′(x)<0	f(x) nghịch biến
(1;2/3)	f′(x)>0	f(x) đồng biến
(2/3;+∞)	f′(x)<0	f(x) nghịch biến

Cực trị:
- Hàm số đạt cực đại tại x=1, giá trị cực đại là f(1) = −2.
- Hàm số đạt cực tiểu tại x=2/3, giá trị cực tiểu là f(2/3)=−5/27

b) Vẽ đồ thị:

Điểm đặc biệt:
- Đồ thị cắt trục Oy tại điểm (0,−5).
- Điểm uốn: (1,−2).
- Tiệm cận ngang: y = 1.
Dựa vào bảng biến thiên và các điểm đặc biệt, vẽ đồ thị hàm số.

Bài 2. Cho hàm số \(g(x) = x^2-2x+3/x -1\)

a) Tìm tập xác định của hàm số g(x).
b) Khảo sát sự biến thiên của hàm số g(x) trên tập xác định.
c) Vẽ đồ thị hàm số g(x).

Lời giải:

a) Tập xác định: D = R \ {1}.
b) Khảo sát sự biến thiên:

Đạo hàm: \(g(x) = 2(x−3)/(x-1)^2\)

Cực trị:

Hàm số đạt cực đại tại x=1, giá trị cực đại là g(1)=4.
Hàm số đạt cực tiểu tại x=3, giá trị cực tiểu là g(3)=2.

c) Vẽ đồ thị:

Điểm đặc biệt:
- Đồ thị cắt trục Oy tại điểm (0,3).
- Tiệm cận đứng: x = 1.
- Tiệm cận ngang: y = 2.
Dựa vào bảng biến thiên và các điểm đặc biệt, vẽ đồ thị hàm số.