Lý thuyết về đường tròn ngoại tiếp và đường tròn nội tiếp - Toán lớp 9

Đường tròn ngoại tiếp đóng vai trò quan trọng trong việc nghiên cứu các tính chất của đa giác, đặc biệt là tứ giác nội tiếp. Hiểu biết về đường tròn ngoại tiếp giúp giải quyết nhiều bài toán hình học phức tạp. Bài viết này sẽ trình bày các kiến thức cơ bản về đường tròn ngoại tiếp tứ giác nội tiếp, bao gồm: định nghĩa, tính chất, dấu hiệu nhận biết, cách vẽ và ứng dụng.

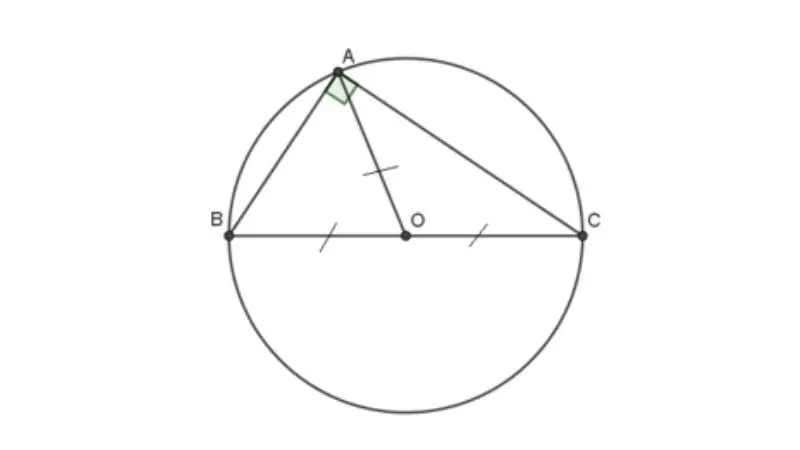
Đường tròn ngoại tiếp 

Định nghĩa đường tròn ngoại tiếp

Đường tròn ngoại tiếp là một đường tròn có bán kính bằng đoạn thẳng nối hai điểm của một hình học, nhưng không chứa bất kỳ điểm nào của hình học đó bên trong hay trên đường tròn đó. Nói cách khác, đường tròn ngoại tiếp của một hình học là một đường tròn chứa hình học đó bên ngoài, chính xác là nó tiếp xúc với hình học ở một điểm.

Ví dụ:

Trong tam giác

ABC, nếu ta vẽ ba đường phân giác từ các đỉnh A,B,C và nói rằng ba đường phân giác gặp nhau tại một điểm O, thì đường tròn ngoại tiếp của tam giác ABC sẽ là đường tròn có tâm là O và bán kính là OA=OB=OC.

Đường tròn ngoại tiếp thường xuất hiện trong nhiều vấn đề hình học, và chúng có một số tính chất đặc biệt quan trọng trong việc giải quyết các bài toán hình học phức tạp.

Tính chất 

Tính chất cơ bản của đường tròn ngoại tiếp liên quan đến mối quan hệ giữa các phần tử của hình học với đường tròn ngoại tiếp. Dưới đây là một số tính chất quan trọng:

Tiếp xúc: Đường tròn ngoại tiếp của một hình học tiếp xúc với hình học đó tại một điểm duy nhất. Điểm tiếp xúc này là điểm duy nhất trên đường tròn ngoại tiếp mà nằm trên hình học và không nằm bên trong hình học đó.

 Đường phân giác: Đường phân giác của một góc trong hình học cắt đường tròn ngoại tiếp tại hai điểm trên đường tròn, và điểm cắt nhau của hai đường phân giác là tâm của đường tròn ngoại tiếp.

Tâm của đường tròn ngoại tiếp: Tâm của đường tròn ngoại tiếp của một hình học là trung điểm của hai điểm tiếp xúc giữa đường tròn và hình học.

Khoảng cách: Khoảng cách từ tâm của đường tròn ngoại tiếp đến mỗi điểm tiếp xúc bằng bán kính của đường tròn.

Góc tạo bởi tiếp tuyến và dây cung: Góc tạo bởi một tiếp tuyến và một dây cung từ một điểm nằm bên ngoài đường tròn bằng một nửa số đo của dây cung.

Tính chất tứ giác ngoại tiếp: Nếu một tứ giác là tứ giác ngoại tiếp, tức là các đỉnh của tứ giác nằm trên một đường tròn ngoại tiếp, thì tứ giác đó là một tứ giác nội tiếp của đường tròn ngoại tiếp.

Dấu hiệu nhận biết

• Tứ giác có tổng số đo hai góc đối bằng \(180^\circ\)
  thì nội tiếp được trong một đường tròn.
• Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại dưới cùng một góc thì nội tiếp được trong một đường tròn.
• Tứ giác có bốn đỉnh cách đều một điểm (mà ta có thể xác định được) thì nội tiếp được trong một đường tròn. Điểm đó là tâm của đường tròn ngoại tiếp tứ giác.
• Đường tròn nội tiếp: là đường tròn nằm bên trong đa giác và tiếp xúc với tất cả các cạnh của đa giác.
• Tâm đường tròn nội tiếp: là giao điểm của các đường phân giác ngoài của đa giác.
• Bán kính đường tròn nội tiếp: có thể được tính bằng công thức: r =\(\frac{K}{p}\)

Trong đó:

K là diện tích của đa giác

p là chu vi của đa giác

Dạng bài tập liên quan

Cho tam giác ABC có AB = 3cm, BC = 4cm, CA = 5cm. Tìm tâm và bán kính của đường tròn ngoại tiếp tam giác ABC.

Giải:

Tính diện tích tam giác ABC:

\(K = \sqrt{p(p – a)(p – b)(p – c)} = \sqrt{6(6 – 3)(6 – 4)(6 – 5)} = 6\)

Tính bán kính đường tròn ngoại tiếp:

\(R = \frac{abc}{4K} = \frac{3 \times 4 \times 5}{4 \times 6} = 2.5\)

Tâm đường tròn ngoại tiếp là giao điểm của các đường phân giác trong của tam giác ABC.

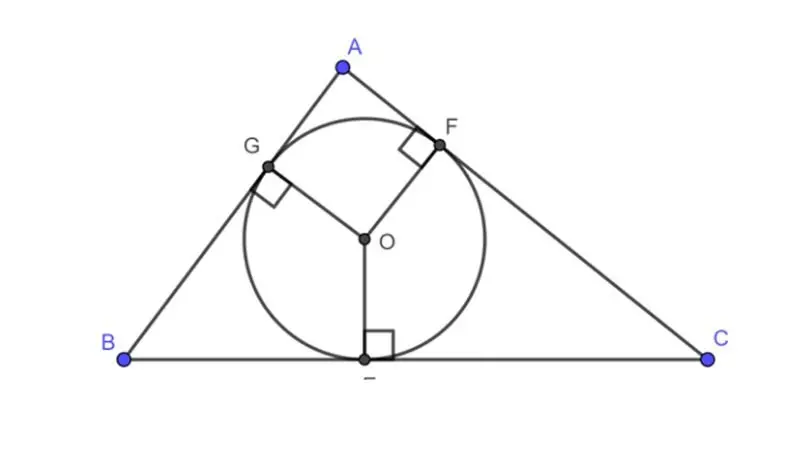
Đường tròn nội tiếp

Định nghĩa đường tròn nội tiếp

Đường tròn nội tiếp là một đường tròn mà các điểm của hình học đều nằm bên trong hoặc trên đường tròn đó. Nói cách khác, đường tròn nội tiếp của một hình học là một đường tròn mà tất cả các điểm của hình học đó đều nằm bên trong hoặc trên đường tròn đó. Đặc điểm quan trọng của đường tròn nội tiếp là nó chứa hình học mà không tiếp xúc với đường tròn ở bên ngoài.

Ví dụ:

Trong tam giác ABC, đường tròn nội tiếp là đường tròn có tâm là trọng tâm của tam giác ABC và đi qua các đỉnh của tam giác đó.

Tính chất

Tiếp xúc: Đường tròn nội tiếp của một hình học tiếp xúc với hình học đó tại một điểm duy nhất. Điểm tiếp xúc này là điểm duy nhất trên đường tròn nội tiếp mà nằm trên hình học và không nằm bên ngoài hình học đó.

 Đường phân giác: Đường phân giác của một góc trong hình học cắt đường tròn nội tiếp tại hai điểm trên đường tròn, và điểm cắt nhau của hai đường phân giác là tâm của đường tròn nội tiếp.

Tâm của đường tròn nội tiếp: Tâm của đường tròn nội tiếp của một hình học là trung điểm của hai điểm tiếp xúc giữa đường tròn và hình học.

Khoảng cách: Khoảng cách từ tâm của đường tròn nội tiếp đến mỗi điểm tiếp xúc bằng bán kính của đường tròn.

Góc tạo bởi tiếp tuyến và dây cung: Góc tạo bởi một tiếp tuyến và một dây cung từ một điểm nằm bên ngoài đường tròn bằng một nửa số đo của dây cung.

Tính chất tứ giác nội tiếp: Nếu một tứ giác là tứ giác nội tiếp, tức là các đỉnh của tứ giác nằm trên một đường tròn nội tiếp, thì tứ giác đó là một tứ giác nội tiếp của đường tròn nội tiếp.

Quan hệ giữa góc và dây cung:Góc tạo bởi hai dây cung bằng một nửa tổng các dây cung tương ứng.

Bán kính đường tròn nội tiếp: Bán kính đường tròn nội tiếp có thể được tính bằng công thức:

          \(r = \frac{K}{p}\)

Trong đó:

K là diện tích của đa giác

p là chu vi của đa giác

Dấu hiệu nhận biết 

• Tứ giác có hai đường chéo vuông góc với nhau thì nội tiếp được trong một đường tròn.
• Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường thì nội tiếp được trong một đường tròn.
• Tứ giác có tổng số đo hai góc đối bằng 180° thì nội tiếp được trong một đường tròn.
• Tứ giác có bốn đỉnh cách đều một điểm (mà ta có thể xác định được) thì nội tiếp được trong một đường tròn. Điểm đó là tâm của đường tròn nội tiếp tứ giác.

Dạng bài liên quan

Cho tam giác ABC có AB = 3cm, BC = 4cm, CA = 5cm. Tìm tâm và bán kính của đường tròn nội tiếp tam giác ABC.

Giải:

Tính diện tích tam giác ABC:

\(K = \sqrt{p(p – a)(p – b)(p – c)} = \sqrt{6(6 – 3)(6 – 4)(6 – 5)} = 6\)

Tính bán kính đường tròn nội tiếp:

\(R = \frac{abc}{4K} = \frac{3 \cdot 4 \cdot 5}{4 \cdot 6} = 2.5\)

Tâm đường tròn nội tiếp là giao điểm của các đường phân giác ngoài của tam giác ABC.

Qua bài viết này, chúng ta đã nắm được các kiến thức cơ bản về đường tròn ngoại tiếp tứ giác nội tiếp. Đây là một chủ đề quan trọng trong hình học và có nhiều ứng dụng thực tế. Hy vọng bài viết này đã giúp ích cho các bạn trong việc học tập và nghiên cứu.