Trong chương trình toán học của lớp 10, một trong những chủ đề quan trọng và hấp dẫn nhất là hàm số bậc hai. Hàm số này, còn được biết đến với tên gọi là “hàm số parabol”, đóng vai trò quan trọng trong việc giải quyết các bài toán liên quan đến vị trí, hình dạng và đồng biến – nghịch biến của đồ thị. Việc hiểu và áp dụng hàm số bậc hai không chỉ là một phần quan trọng của chương trình học mà còn giúp học sinh phát triển kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Định nghĩa hàm số bậc hai
Hàm số bậc hai lớp 10 được định nghĩa là dạng hàm số có công thức tổng quát là \(y = ax^2 + bx + c\), trong đó a,b,c là hằng số cho trước, a ≠ 0.
Tập xác định của hàm số bậc hai lớp 10 là: D = R
Biệt thức \(Delta: = b^2-4ac\)
Chiều biến thiên và bảng biến thiên
Cho hàm số bậc hai \(y = ax^2 + bx + c\) VỚI a > 0, chiều biến thiên của hàm só bậc hai lớp 10 khi đó là:
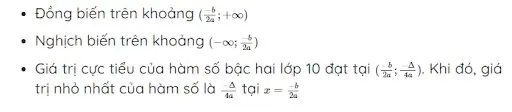
Cho hàm số \(y = ax^2 + bx + c\) Với a < 0, chiều biến thiên của hàm số bậc hai lớp 10 khi đó là:
Đồ thị hàm số bậc hai
| Hàm số | Đỉnh parabol | Trục đối xứng | Giao điểm với trục tung | Giao điểm với trục hoành | Bề lõm | Chiều biến thiên |
| \(y = ax^2 + bx + c (a > 0)\) | \((-b/2a; -Δ/4a)\) | \(x = -b/2a\) | (0; c) | Nghiệm của \(ax^2 + bx + c = 0\) | Quay lên trên | – Đồng biến trên (-∞; -b/2a) và (a; ∞) <br> – Nghịch biến trên (-b/2a; ∞) |
| \(y = ax^2 + bx + c (a < 0)\) | \((-b/2a; -Δ/4a)\) | \(x = -b/2a\) | (0; c) | Nghiệm của \(ax^2 + bx + c = 0\) | Quay xuống dưới | – Đồng biến trên (-b/2a; ∞) <br> – Nghịch biến trên (-∞; -b/2a) |
Các dạng bài tập hàm số bậc hai lớp 10
Dạng 1: Xác định tập xác định của hàm số
Ví dụ: Xác định tập xác định của hàm số \(y = √(x^2 – 4)\).
Lời giải:
Hàm số \(y = √(x^2 – 4)\) xác định khi và chỉ khi \(x^2 – 4 ≥ 0\).
⇔ \((x – 2)(x + 2) ≥ 0\)
⇔ x ≤ -2 hoặc x ≥ 2.
Vậy tập xác định của hàm số là D = (-∞; -2] ∪ [2; ∞).
Dạng 2: Tìm tập giá trị của hàm số
Ví dụ: Tìm tập giá trị của hàm số \(y = x^2 – 4x + 3\).
Lời giải:
- Ta có: \(y = x^2 – 4x + 3 = (x^2 – 4x + 4) – 1 = (x – 2)^2 – 1\).
Vì \((x – 2)^2 ≥ 0\) với mọi x, nên \((x – 2)^2 – 1 ≥ -1 với mọi x\).
Vậy tập giá trị của hàm số là T = [-1; ∞).
Dạng 3: Lập đồ thị hàm số
Ví dụ: Lập đồ thị hàm số \(y = -x^2 + 4x – 3\).
Lời giải:
- Bước 1: Tìm tọa độ đỉnh parabol.
- \(Δ = b^2 – 4ac = 4^2 – 4(-1)(-3) = 20\).
- \(x = -b/2a = -4/(-2) = 2\).
- \(y = -a(x – 2)^2 + (-1)(-2)^2 – 3 = -1\).
Vậy đỉnh parabol là (2; -1).
- Bước 2: Vẽ trục đối xứng.
Trục đối xứng là đường thẳng x = 2.
- Bước 3: Vẽ parabol.
Parabol đi qua điểm (0; -3) và (4; -3).
- Bước 4: Xác định chiều biến thiên.
Hàm số \(y = -x^2 + 4x – 3\) nghịch biến trên khoảng (-∞; 2) và đồng biến trên khoảng (2; ∞).
Vậy đồ thị hàm số \(y = -x^2 + 4x – 3\) như sau:
Dạng 4: Giải phương trình bậc hai
Ví dụ: Giải phương trình \(x^2 – 4x + 3 = 0\).
Lời giải:
- Ta có: a = 1, b = -4, c = 3.
- \(Δ = b^2 – 4ac = (-4)^2 – 4(1)(3) = 4\).
- \(x1,2 = (-b ± √Δ)/2a = (4 ± √4)/2 = 2 ± √1\).
Vậy nghiệm của phương trình là \(x1 = 2 + √1 và x2 = 2 – √1\).
Dạng 5: Ứng dụng
Ví dụ: Một quả bóng được ném lên cao từ mặt đất. Hỏi sau 2 giây, quả bóng đạt độ cao bao nhiêu?
Lời giải:
- Gọi h(t) là độ cao của quả bóng tại thời điểm t (giây).
- Ta có: \(h(t) = -4,9t^2 + v0t + h0\).
- Biết v0 = 19,6 m/s (vận tốc ban đầu) và h0 = 1,2 m (độ cao ban đầu).
- Sau 2 giây, quả bóng đạt độ cao:
\(h(2) = -4,9 x 2^2 + 19,6 x 2 + 1,2 = 28,4 m\).
Tóm lại, hàm số bậc hai là một chủ đề quan trọng và thú vị trong chương trình toán học lớp 10. Việc hiểu sâu về cấu trúc và tính chất của hàm số này không chỉ giúp học sinh vững chắc hơn trong môn toán mà còn mở ra cánh cửa cho việc áp dụng trong các lĩnh vực khác như vật lý, kinh tế và thống kê.
