Lý thuyết hai tam giác bằng nhau - Bài tập và phương pháp giải

Hai tam giác bằng nhau là một trong những khái niệm cơ bản và quan trọng nhất trong môn Toán học lớp 7. Nó là nền tảng cho nhiều định lý, tính chất và bài toán liên quan đến tam giác.

Định nghĩa hai tam giác bằng nhau

Hai tam giác được gọi là bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.

Ký hiệu:

∆ABC = ∆A’B’C’ (đọc là tam giác ABC bằng tam giác A’B’C )

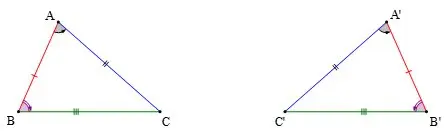
Trường hợp hai tam giác bằng nhau

Có ba trường hợp bằng nhau của tam giác:

Cạnh – cạnh – cạnh (c.c.c)

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

Cạnh – góc – cạnh (c.g.c)

Nếu hai cạnh của tam giác này bằng hai cạnh của tam giác kia và hai góc xen giữa hai cạnh ấy bằng nhau thì hai tam giác đó bằng nhau.

Góc – cạnh – góc (g.c.g)

Nếu hai góc của tam giác này bằng hai góc của tam giác kia và cạnh tương ứng giữa hai góc bằng nhau thì hai tam giác đó bằng nhau.

Cách vẽ tam giác khi biết số đo ba cạnh

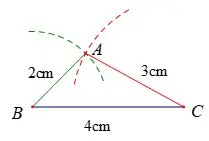
Chẳng hạn: Vẽ tam giác ABC biết AB = 2 cm; AC = 3 cm; BC = 4 cm.

+ Dùng thước kẻ có vạch chia vẽ đoạn BC = 4 cm (hoặc có thể vẽ AB hoặc AC trước)

+ Dùng compa mở khẩu độ 2 cm, tâm tại điểm B, vẽ 1 cung tròn; mở compa khẩu độ 3 cm, tâm tại điểm C, vẽ một cung tròn. Giao điểm của 2 cung tròn là điểm A.

+ Vẽ các đoạn thẳng AB; AC ta được tam giác ABC.

Tính chất hai tam giác bằng nhau

Hai tam giác bằng nhau thì:

• Các cạnh tương ứng bằng nhau.
• Các góc tương ứng bằng nhau.
• Hai đường trung tuyến tương ứng bằng nhau.
• Hai đường phân giác tương ứng bằng nhau.
• Hai đường cao tương ứng bằng nhau.
• Chu vi bằng nhau.
• Diện tích bằng nhau.

Bài tập hai tam giác bằng nhau có lời giải chi tiết

Bài tập 1: Cho tam giác ABC và tam giác MNP có AB = MN, AC = MP, ∠BAC = ∠MNP. Chứng minh ΔABC = ΔMNP.

Lời giải:

Xét ΔABC và ΔMNP có:

AB = MN (theo giả thiết)

AC = MP (theo giả thiết)

∠BAC = ∠MNP (theo giả thiết)

Vậy ΔABC = ΔMNP (c.g.c)

Bài tập 2: Cho tam giác ABC và tam giác DEF có BC = EF, ∠BAC = ∠DEF, ∠ABC = ∠DFE. Chứng minh ΔABC = ΔDEF.

Lời giải:

Xét ΔABC và ΔDEF có:

BC = EF (theo giả thiết)

∠BAC = ∠DEF (theo giả thiết)

∠ABC = ∠DFE (theo giả thiết)

Vậy ΔABC = ΔDEF (g.c.g).

Bài tập 3: Cho tam giác ABC vuông tại A, biết AB = 6cm, AC = 8cm. Tính BC.

Lời giải:

Áp dụng định lý Pytago vào tam giác ABC vuông tại A, ta có:

BC² = AB² + AC² = 6² + 8² = 100

BC = √100 = 10cm

Vậy BC = 10cm

Bài tập 4: Cho tam giác ABC cân tại A, biết ∠B = 70°. Tính ∠A và ∠C.

Lời giải:

Ta có: ∠B + ∠C = 180° – ∠A (tổng ba góc của một tam giác)

Mà ∠B = ∠C (tam giác ABC cân tại A)

Suy ra: 2∠B = 180° – ∠A

Thay ∠B = 70° vào, ta được:

2 * 70° = 180° – ∠A

140° = 180° – ∠A

∠A = 180° – 140° = 40°

Vậy ∠A = 40° và ∠C = ∠B = 70°.

Bài tập 5: Cho tam giác ABC vuông tại A, biết AB = 3cm, AC = 4cm. Tính BC và các góc của tam giác ABC.

Lời giải:

a) Tính BC:

Áp dụng định lý Pytago vào tam giác ABC vuông tại A, ta có:
BC² = AB² + AC² = 3² + 4² = 25

BC = \(\)\frac{25}\(\) = 5cm

Vậy BC = 5cm.

b) Tính các góc của tam giác ABC:

Ta có: ∠A = 90° (tam giác ABC vuông tại A)

Áp dụng tính chất hai góc phụ nhau, ta có:

∠B = 90° – ∠A = 90° – 90° = 0°
∠C = 90° – ∠B = 90° – 0° = 90°
Vậy ∠A = 90°, ∠B = 0° và ∠C = 90°.

Lý thuyết hai tam giác bằng nhau là một trong những kiến thức cơ bản và quan trọng trong môn Toán học lớp 7. Nắm vững kiến thức này sẽ giúp bạn giải quyết nhiều bài toán hình học một cách dễ dàng.